Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải

Việc nắm vững **công thức tính thể tích hình cầu** giúp giải quyết nhiều bài toán thực tế trong cuộc sống. Bài viết trình bày chi tiết các phương pháp tính toán đơn giản, kèm theo ví dụ minh họa cụ thể về cách áp dụng công thức vào thực tiễn như tính thể tích quả bóng tennis hay quả địa cầu.

Thể tích hình cầu là gì? Tìm hiểu khái niệm và đặc điểm cơ bản

Thể tích hình cầu là phần không gian bên trong hình cầu, được tính bằng công thức

Bạn đang xem: Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải

V = (4/3)πR³

Trong đó R là bán kính của hình cầu. Đây là một trong những công thức quan trọng mà các em cần ghi nhớ khi học về hình học không gian.

Khi tìm hiểu về thể tích cầu là gì, chúng ta cần hiểu rằng đây là thể tích của một khối tròn xoay hoàn hảo, được tạo thành khi xoay một nửa hình tròn quanh đường kính của nó. Tất cả các điểm trên bề mặt hình cầu đều cách đều tâm một khoảng bằng bán kính.

Để dễ hình dung, tôi thường lấy ví dụ về quả bóng tennis. Khi bạn cầm một quả bóng tennis trên tay, phần không gian bên trong lớp vỏ màu vàng chính là thể tích của hình cầu đó. Nếu ta đổ đầy nước vào một quả bóng rỗng có cùng kích thước, lượng nước chứa được chính là thể tích của hình cầu.

Một điểm đặc biệt về thể tích hình cầu là nó có tỷ lệ với lập phương của bán kính. Điều này có nghĩa khi bán kính tăng gấp đôi, thể tích sẽ tăng gấp 8 lần. Đó là lý do vì sao các vật thể hình cầu trong tự nhiên thường có kích thước khá cân đối và ổn định.

Công thức tính thể tích hình cầu và các thành phần liên quan

Hình cầu là một khối tròn xoay hoàn hảo trong không gian ba chiều, được tạo thành từ tất cả các điểm cách đều một điểm cố định gọi là tâm. Công thức tính thể tích hình cầu phụ thuộc vào bán kính hoặc đường kính của hình cầu đó. Để tính được thể tích, chúng ta cần nắm rõ các yếu tố cấu thành và mối quan hệ giữa chúng.

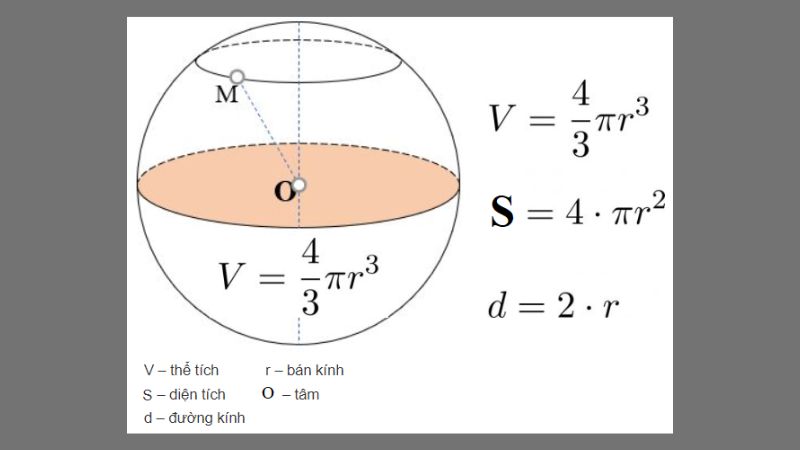
Các yếu tố cần biết trong công thức thể tích hình cầu

Trước khi đi vào các công thức cụ thể, việc hiểu rõ các thành phần của hình cầu sẽ giúp quá trình tính toán trở nên dễ dàng hơn. Bán kính (R) là khoảng cách từ tâm đến một điểm bất kỳ trên mặt cầu, trong khi đường kính (D) bằng hai lần bán kính. Ngoài ra, công thức tính diện tích mặt cầu cũng có mối liên hệ mật thiết với thể tích của nó.

Công thức tính thể tích hình cầu theo bán kính

Công thức tính thể tích khối cầu theo bán kính được biểu diễn bằng công thức

Xem thêm : Công thức tính diện tích xung quanh hình nón và bài tập hướng dẫn chi tiết

V = (4/3)πR³

Trong đó R là bán kính và π ≈ 3,14.

Công thức này xuất phát từ phép tính tích phân quay, giúp xác định chính xác thể tích của một khối cầu hoàn chỉnh. Với công thức đơn giản này, việc tính toán trở nên thuận tiện cho mọi bài toán liên quan.

Công thức tính thể tích hình cầu theo đường kính

Khi biết đường kính D của hình cầu, ta có thể tính thể tích theo công thức

V = (1/6)πD³

Công thức này được rút ra từ mối quan hệ D = 2R và thay thế vào công thức tính theo bán kính. Việc sử dụng đường kính thay vì bán kính đôi khi thuận tiện hơn trong một số trường hợp thực tế.

Bài tập mẫu về tính thể tích hình cầu theo bán kính và đường kính

Ví dụ 1: Một quả bóng có bán kính 5cm, tính thể tích của quả bóng.
Giải:
V = (4/3)π × 5³
V = (4/3) × 3,14 × 125
V ≈ 523,33 cm³

Ví dụ 2: Một quả cầu có đường kính 10cm, tính thể tích của quả cầu.
Giải:
V = (1/6)π × 10³
V = (1/6) × 3,14 × 1000
V ≈ 523,33 cm³

Hướng dẫn chi tiết cách tính thể tích hình cầu qua ví dụ thực tế

Việc tính cách tính thể tích hình cầu có thể gây khó khăn cho nhiều học sinh. Tuy nhiên, với công thức V = (4/3)πr³, chúng ta có thể dễ dàng tính được thể tích của bất kỳ hình cầu nào khi biết bán kính.

Các bước tính thể tích hình cầu cơ bản

Để tính thể tích quả cầu, trước tiên cần xác định bán kính r của hình cầu. Nếu chỉ biết đường kính d, ta chia đôi để có r = d/2. Sau đó, lập tức áp dụng công thức

V = (4/3)πr³

Xem thêm : Khám phá công thức tính diện tích xung quanh hình trụ và bài tập ứng dụng

Với π ≈ 3,14, ta sẽ có kết quả chính xác. Ngoài ra, bạn có thể tham khảo thêm diện tích hình cầu theo đường kính để hiểu rõ hơn mối quan hệ giữa diện tích và thể tích.

Ví dụ tính thể tích quả bóng tennis

Một quả bóng tennis tiêu chuẩn có đường kính 6,7cm. Để tính thể tích:

– Bước 1: Tính bán kính r = 6,7/2 = 3,35cm
– Bước 2: Áp dụng công thức V = (4/3) × 3,14 × 3,35³
– Bước 3: Kết quả V ≈ 157,4cm³

Ví dụ tính thể tích quả địa cầu

Theo NASA, Trái Đất có bán kính trung bình khoảng 6.371km. Ta có:
– Bước 1: Chuyển đơn vị sang km
– Bước 2: V = (4/3) × 3,14 × 6.371³
– Bước 3: Kết quả V ≈ 1.083 tỷ km³

Kết quả này giúp ta hiểu được quy mô khổng lồ của Trái Đất so với các vật thể thông thường xung quanh.

Mối quan hệ giữa thể tích và diện tích hình cầu

Khi nghiên cứu về hình cầu, chúng ta sẽ thấy mối liên hệ chặt chẽ giữa thể tích khối cầu và diện tích hình cầu. Hai đại lượng này có mối quan hệ tỷ lệ thuận với nhau, nghĩa là khi bán kính tăng thì cả thể tích và diện tích đều tăng theo một quy luật nhất định.

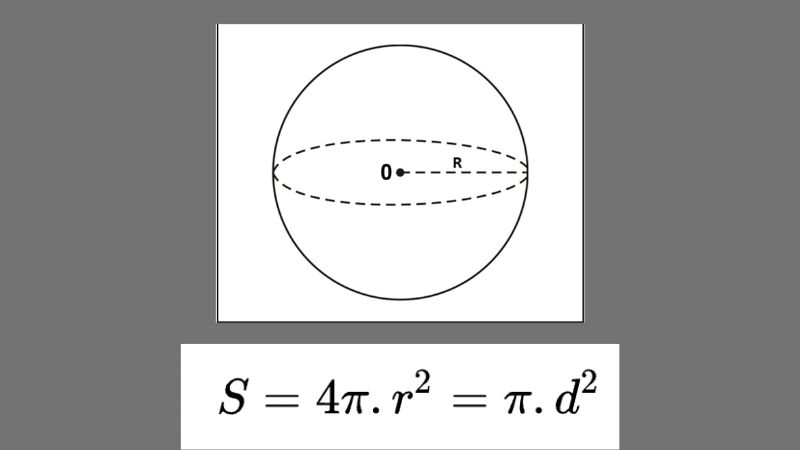
So sánh công thức thể tích và diện tích hình cầu

Công thức tính diện tích và thể tích hình cầu đều phụ thuộc vào bán kính R. Tương tự như thể tích hình trụ là gì, thể tích khối cầu cũng được tính dựa trên số π. Với diện tích hình cầu, công thức là S = 4πR², còn thể tích được tính theo công thức V = 4/3πR³. Điểm đáng chú ý là hệ số 4π xuất hiện trong cả hai công thức, thể hiện mối liên hệ mật thiết giữa chúng.

Bài tập tổng hợp về thể tích và diện tích hình cầu

Bài tập 1: Một quả bóng có bán kính 5cm. Tính diện tích và thể tích của quả bóng.
Giải:
– Diện tích: S = 4π × 5² = 314,16 cm²
– Thể tích: V = 4/3π × 5³ = 523,6 cm³

Bài tập 2: Một hình cầu có thể tích 904,78 cm³. Tính diện tích của hình cầu đó.
Giải:
Từ V = 904,78 cm³, ta tìm được R = 6cm
Thay vào công thức diện tích: S = 4π × 6² = 452,39 cm²

Các bài tập trên minh họa rõ mối quan hệ giữa thể tích và diện tích, giúp học sinh hiểu sâu hơn về tính chất của hình cầu.

FAQ: Câu hỏi thường gặp về cách tính thể tích hình cầu

Khi tìm hiểu về công thức hình cầu, nhiều học sinh thường gặp những thắc mắc cần được giải đáp. Tôi sẽ phân tích từng câu hỏi một cách chi tiết để các em dễ dàng nắm bắt kiến thức.

Làm thế nào để tính thể tích hình cầu khi chỉ biết diện tích?

Để tính thể tích cầu công thức khi biết diện tích, chúng ta cần xác định bán kính từ diện tích trước. Diện tích hình cầu bằng 4πR², từ đó tính được R. Sau khi có R, áp dụng công thức V = 4/3πR³. Tương tự như khi tính công thức khối chóp, việc chuyển đổi từ diện tích sang thể tích luôn cần qua bước trung gian.

Tại sao công thức thể tích hình cầu lại có số π?

Số π xuất hiện trong công thức vì hình cầu là một khối tròn xoay. Khi một nửa hình tròn quay quanh trục đường kính, nó tạo thành hình cầu. Mọi mặt cắt của hình cầu qua tâm đều là hình tròn, và π là tỷ số giữa chu vi và đường kính của hình tròn. Do đó, π trở thành thành phần không thể thiếu trong cách tính quả cầu.

Có thể áp dụng công thức này cho mọi loại hình cầu không?

Công thức V = 4/3πR³ áp dụng cho tất cả hình cầu, không phân biệt kích thước hay chất liệu. Điều kiện duy nhất là hình cầu phải đều và hoàn chỉnh. Với những hình cầu khuyết hoặc bị cắt một phần, ta cần điều chỉnh công thức và thêm các phép tính phụ trợ.

Các kiến thức về **công thức tính thể tích hình cầu** đã được trình bày một cách chi tiết và dễ hiểu thông qua các ví dụ thực tế. Việc nắm vững công thức cơ bản cùng các bước tính toán giúp học sinh dễ dàng áp dụng vào giải các bài toán liên quan đến thể tích, diện tích của hình cầu. Các phương pháp tính toán đơn giản kết hợp với bài tập mẫu tạo nền tảng vững chắc cho việc học tập hình học không gian.

Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian