Công thức tính góc giữa hai mặt phẳng là gì? Hướng dẫn cụ thể

Công thức tính góc giữa hai mặt phẳng là một trong những phương pháp tính toán thuộc hình học không gian. Congthuctoan sẽ giúp bạn hiểu rõ hơn về công thức này cũng như cách áp dụng để giải nhanh gọn bài tập.

Khái niệm công thức tính góc giữa hai mặt phẳng

Công thức tính góc giữa hai mặt phẳng là công thức xác định chính xác số đo của góc được tạo nên bởi hai mặt phẳng đó bằng bao nhiêu.

Bạn đang xem: Công thức tính góc giữa hai mặt phẳng là gì? Hướng dẫn cụ thể

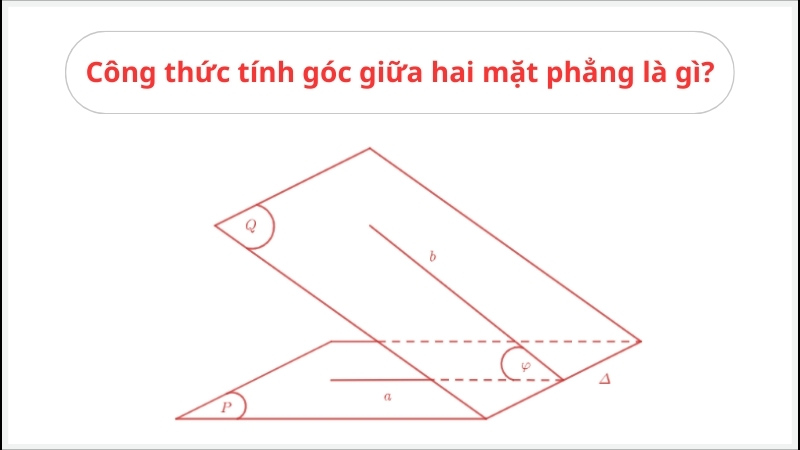
Trước khi đi vào công thức cụ thể thì bạn cần hiểu góc giữa hai mặt phẳng là gì. Góc này được đo dựa trên góc của hai đường thẳng (a và b) nằm trên hai mặt phẳng (P và Q). a và b lần lượt có phương vuông góc với giao tuyến P và Q.

Góc được tạo nên có những đặc điểm như sau ảnh hưởng đến cách xác định số đo:

• Không bao giờ là góc tù;
• Hai mặt phẳng P và Q song song sẽ tạo ra góc bằng 0 độ;
• P và Q trùng nhau tạo nên góc 0 độ;
• P và Q vuông góc với nhau tạo ra góc 90 độ.

Việc xác định công thức cụ thể phải dựa trên phương pháp mà bạn giải bài toán đó. Phổ biến nhất chính là sử dụng vectơ pháp tuyến để xác định giá trị cosin và tính góc.

Cách giải bài toán góc giữa hai mặt phẳng hiệu quả nhất

Không phải lúc nào bạn cũng có thể áp dụng một công thức có sẵn là ra được kết quả. Mặt khác, một số bài toán cần sử dụng phương án phù hợp hơn để tính chính xác độ của góc.

Có bốn cách phổ biến nhất để tìm ra được kết quả cuối cùng bài toán hình học không gian.

Cách 1: Với công thức tính góc giữa hai mặt phẳng dựa trên vectơ, bạn sẽ áp dụng theo trình tự như sau:

• Bạn cần tìm vectơ pháp tuyến của hai mặt phẳng đã cho thông qua hệ số phương trình ban đầu.
• Từ giá trị cos có được bạn tính góc chính xác.

Xem thêm : Tìm hiểu chi tiết công thức tích có hướng kèm bài tập và lời giải chi tiết

Cách 2: Bạn dựng thêm một mặt phẳng phụ để rồi tính góc tạo ra:

• Dựng mặt phẳng mới vuông góc với giao tuyến của hai mặt phẳng ban đầu.
• Xác định giao tuyến mặt phải phụ với hai mặt phẳng đã cho.
• Tính góc giữa hai giao tuyến.

Cách 3: Công thức hình chiếu cực kỳ hữu dụng:

• Tính diện tích hình chiếu lần lượt trên mặt phẳng thứ nhất và mặt phẳng thứ hai.
• Áp dụng công thức liên quan giữa diện tích hai hình chiếu để tính góc.

Cách 4: Ứng dụng đường thẳng vuông góc:

• Tìm hai đường thẳng a và b vuông góc với giao tuyến của hai mặt phẳng đang có.
• Tính góc giữa hai đường thẳng đó là ra góc giữa hai mặt phẳng.

Ứng dụng công thức tính góc giữa hai mặt phẳng trong thực tế

Hình học không gian xuất hiện rất nhiều trong các lĩnh vực cuộc sống và sản xuất. Phổ biến nhất phải kể tới thiết kế công trình, xây dựng nhà ở được thực hiện hàng ngày.

Việc tính góc giữa các mặt phẳng khi dựng tường, làm cột,… đảm bảo tính chắc chắn và thẩm mỹ của ngôi nhà.

Hay cả trong việc thiết kế nội thất thì ứng dụng công thức hình học cũng rất quan trọng. Ví dụ việc đặt một chiếc bàn, một chiếc ghế sofa sao cho tối ưu công năng và diện tích phải dựa trên số liệu cụ thể.

Góc giữa hai mặt phẳng còn xuất hiện trong lĩnh vực kỹ thuật, bao gồm lắp ráp máy móc thiết bị, tính góc của bánh răng, tạo trục khuỷu,…

Cầu đường cũng là lĩnh vực cần được ứng dụng công thức tính góc giữa hai mặt phẳng. Chẳng hạn khi xây cầu treo, cầu vượt sông nếu không đáp ứng được góc nghiêng phù hợp sẽ giảm đi tải trọng có thể chịu.

Bài tập minh hoạ cùng lời giải ngắn gọn

Xem thêm : Công thức tính góc giữa hai đường thẳng kèm bài tập minh họa

Tùy vào đề bài như thế nào mà bạn có thể áp dụng một trong bốn phương pháp được đề cập phía trên. Ứng dụng công thức dành cho dạng đề dễ nhất, có thể tính được vectơ pháp tuyến.

Một số ví dụ Congthuctoan đưa ra sẽ giúp bạn:

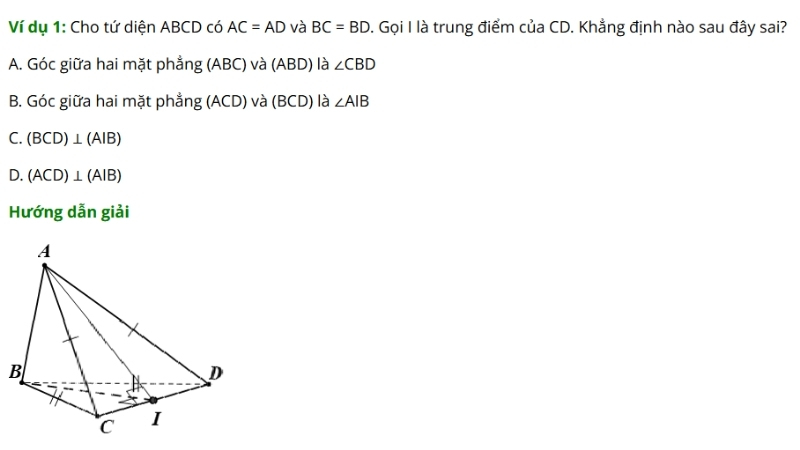
Đề 1:

Đề 2:

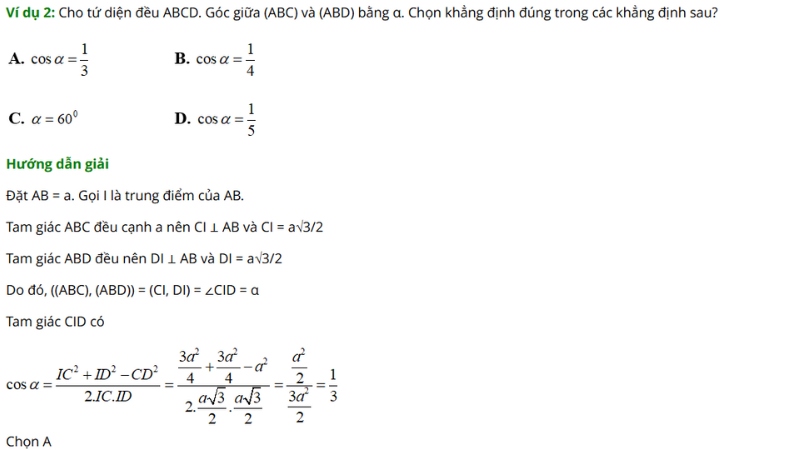
Kết luận

Công thức tính góc giữa hai mặt phẳng là một trong những kiến thức quan trọng của Toán hình học. Bạn nên dành nhiều thời gian luyện đề có các bài tập không gian để hiểu sâu bản chất.

Nguồn: https://congthuctoan.com
Danh mục: Góc và vectơ