Tổng hợp công thức tính độ lệch chuẩn và phương sai trong thống kê cho học sinh

Phương pháp áp dụng **công thức tính độ lệch chuẩn và phương sai** giúp đánh giá mức độ phân tán của dữ liệu trong thống kê. Bài viết trình bày chi tiết các bước tính toán kèm ví dụ minh họa cụ thể, phù hợp cho học sinh và sinh viên nắm bắt kiến thức cơ bản về hai đại lượng thống kê quan trọng này.

Tìm hiểu về độ lệch chuẩn và phương sai trong thống kê

Độ lệch chuẩn và phương sai là hai chỉ số thống kê quan trọng giúp đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Khi tôi giảng dạy cho học sinh, tôi thường ví von chúng như “thước đo” sự dao động của điểm số trong lớp học.

Bạn đang xem: Tổng hợp công thức tính độ lệch chuẩn và phương sai trong thống kê cho học sinh

Phương sai (variance) là trung bình của bình phương các độ lệch so với giá trị trung bình. Nói đơn giản hơn, phương sai cho biết các số liệu trong tập dữ liệu “xa” giá trị trung bình đến mức nào. Công thức tính độ lệch chuẩn và phương sai có mối liên hệ chặt chẽ với nhau – độ lệch chuẩn chính là căn bậc hai của phương sai.

Ví dụ: Một lớp học có 5 học sinh với điểm số: 7, 8, 8, 9, 8
– Giá trị trung bình = (7 + 8 + 8 + 9 + 8)/5 = 8
– Phương sai = [(7-8)² + (8-8)² + (8-8)² + (9-8)² + (8-8)²]/5 = 0.4
– Độ lệch chuẩn = √0.4 ≈ 0.63

Khi phương sai và độ lệch chuẩn có giá trị nhỏ, điều đó phản ánh điểm số của các học sinh khá đồng đều. Ngược lại, giá trị lớn cho thấy có sự chênh lệch đáng kể giữa các điểm số. Đây là công cụ hữu ích giúp giáo viên đánh giá được mức độ tiếp thu kiến thức của cả lớp.

Phương sai và độ lệch chuẩn – Hai đại lượng thống kê quan trọng trong phân tích dữ liệu

Phương sai và độ lệch chuẩn là hai công cụ thống kê cơ bản giúp đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Tương tự như cách tính công thức tính khoảng cách từ điểm đến đường thẳng, hai đại lượng này cho biết các giá trị trong tập dữ liệu “xa” trung bình như thế nào.

Phương sai và độ lệch chuẩn trong thống kê có mối quan hệ mật thiết với nhau. Phương sai là trung bình của bình phương độ lệch so với giá trị trung bình, trong khi độ lệch chuẩn là căn bậc hai của phương sai. Ví dụ khi phân tích điểm thi của một lớp học, phương sai 100 và độ lệch chuẩn 10 cho thấy điểm số của học sinh dao động trung bình khoảng 10 điểm so với điểm trung bình của lớp.

Độ lệch chuẩn và phương sai thường được sử dụng song song trong phân tích thống kê. Phương sai giúp đánh giá tổng quát về độ phân tán, nhưng do đơn vị bình phương nên khó diễn giải trực quan. Độ lệch chuẩn có cùng đơn vị với dữ liệu gốc nên dễ hiểu hơn. Theo nghiên cứu của Viện Khoa học Thống kê Mỹ, khoảng 68% dữ liệu thường nằm trong khoảng một độ lệch chuẩn so với giá trị trung bình.

Công thức tính phương sai và các bước thực hiện chi tiết

Phương sai là một khái niệm thống kê quan trọng giúp đánh giá mức độ phân tán của dữ liệu. Để tính được phương sai chính xác, chúng ta cần nắm vững định nghĩa và các bước thực hiện cụ thể.

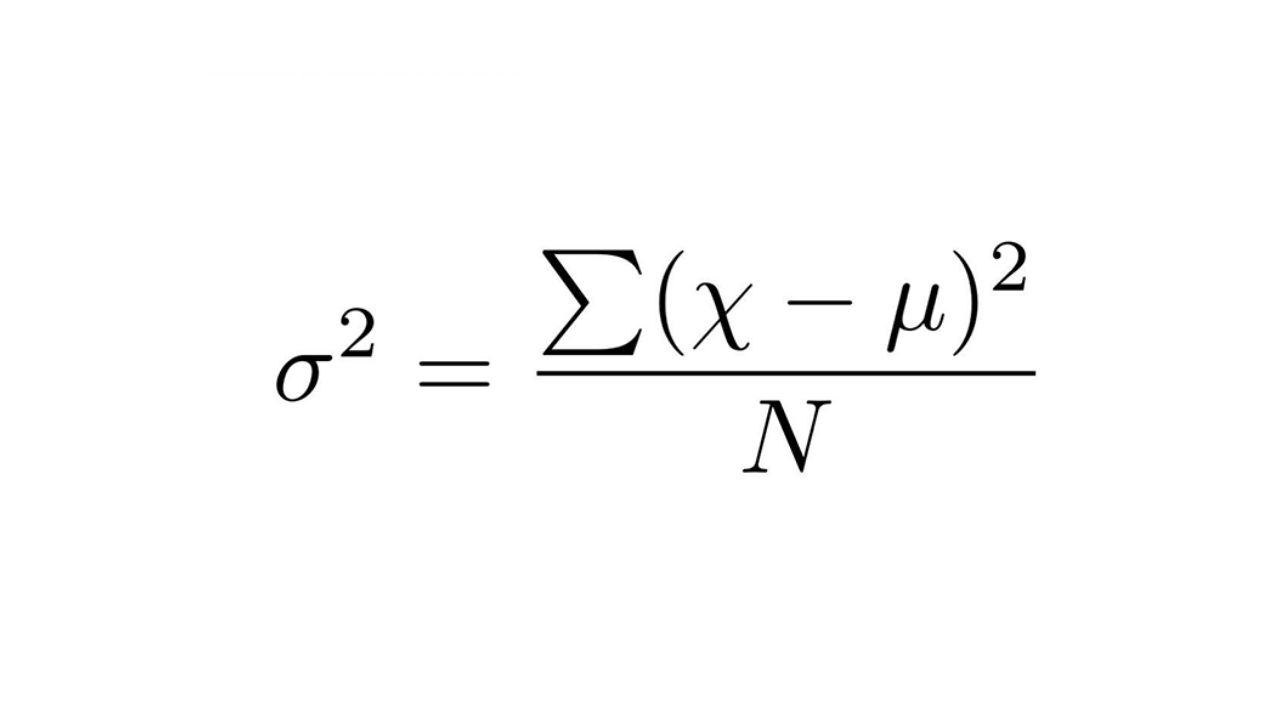
Phương sai là gì và ý nghĩa trong thống kê

Phương sai là đại lượng đo lường mức độ biến thiên của các giá trị trong một tập dữ liệu so với giá trị trung bình. Khi các số liệu phân tán rộng, phương sai sẽ lớn. Ngược lại, nếu các số liệu tập trung gần giá trị trung bình, phương sai sẽ nhỏ.

Công thức tính phương sai tổng quát

Cách tính phương sai được thực hiện qua công thức:

Xem thêm : Lý thuyết công thức tỉ lệ thuận Toán lớp 7

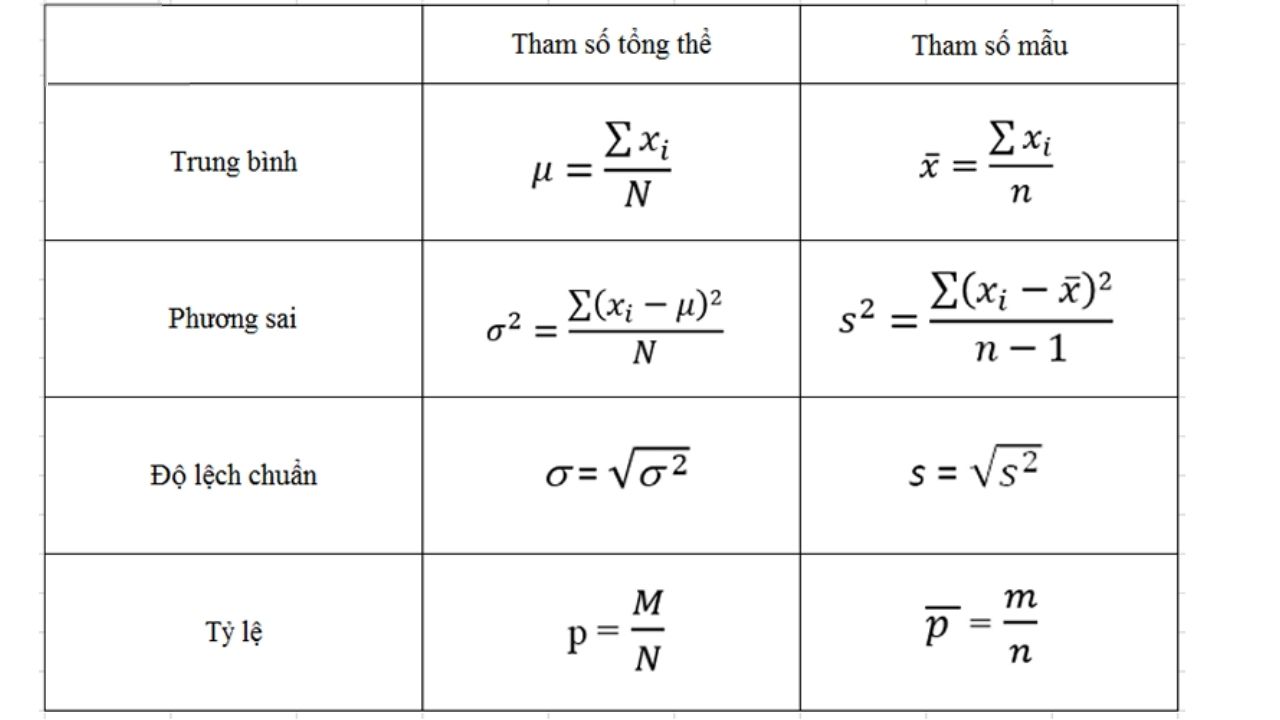
σ² = Σ(x – μ)²/n

Trong đó:
– σ² là phương sai
– x là giá trị của từng phần tử
– μ là giá trị trung bình của tập dữ liệu
– n là số lượng phần tử

Tương tự như công thức tính khoảng cách từ điểm đến mặt phẳng, công thức tính phương sai cũng đòi hỏi sự tỉ mỉ trong từng bước tính toán.

Ví dụ minh họa cách tính phương sai

Bài tập mẫu 1: Tính phương sai của dãy số

Cho dãy số: 2, 4, 6, 8, 10
Bước 1: Tính giá trị trung bình μ = (2+4+6+8+10)/5 = 6
Bước 2: Tính (x-μ)² cho từng số:
(2-6)² = 16
(4-6)² = 4
(6-6)² = 0
(8-6)² = 4
(10-6)² = 16
Bước 3: Tính phương sai σ² = (16+4+0+4+16)/5 = 8

Bài tập mẫu 2: Tính phương sai trong bài toán thực tế

Một cửa hàng ghi nhận doanh thu 5 ngày (đơn vị: triệu đồng): 15, 18, 20, 17, 15
Bước 1: Tính trung bình μ = (15+18+20+17+15)/5 = 17
Bước 2: Tính (x-μ)² cho từng số:
(15-17)² = 4
(18-17)² = 1
(20-17)² = 9
(17-17)² = 0
(15-17)² = 4
Bước 3: Tính phương sai σ² = (4+1+9+0+4)/5 = 3.6

Hướng dẫn chi tiết cách tính độ lệch chuẩn từ phương sai

Việc tính toán độ lệch chuẩn từ phương sai là một kỹ năng quan trọng trong thống kê. Tôi sẽ hướng dẫn các em từng bước một cách chi tiết và dễ hiểu nhất.

Độ lệch chuẩn là gì và ý nghĩa thống kê

Độ lệch chuẩn là một chỉ số thống kê quan trọng đo lường mức độ phân tán của dữ liệu so với giá trị trung bình. Giống như một thước đo sự biến động, nó cho biết các giá trị trong tập dữ liệu phân tán rộng hay tập trung gần giá trị trung bình.

Trong thực tế, các nhà nghiên cứu thường sử dụng công thức tính độ lệch chuẩn và phương sai để đánh giá độ tin cậy của dữ liệu. Ví dụ như trong ngành giáo dục, độ lệch chuẩn giúp đánh giá sự chênh lệch điểm số giữa các học sinh.

Công thức tính độ lệch chuẩn từ phương sai

Cách tính độ lệch chuẩn đơn giản là lấy căn bậc hai của phương sai. Tương tự như công thức tính khoảng cách giữa hai đường thẳng, độ lệch chuẩn cũng sử dụng phép khai căn.

Công thức:

σ = √s²

Trong đó:
– σ là độ lệch chuẩn
– s² là phương sai

Các bước tính độ lệch chuẩn chi tiết

Để tính độ lệch chuẩn, ta thực hiện theo trình tự:

• Tính giá trị trung bình của tập dữ liệu

• Tính phương sai

• Lấy căn bậc hai của phương sai

Bài tập mẫu 3: Tính độ lệch chuẩn của dãy số

Cho dãy số: 2, 4, 6, 8, 10
– Giá trị trung bình = (2+4+6+8+10)/5 = 6
– Phương sai = [(2-6)²+(4-6)²+(6-6)²+(8-6)²+(10-6)²]/5 = 8
– Độ lệch chuẩn = √8 ≈ 2.83

Bài tập mẫu 4: Ứng dụng độ lệch chuẩn trong thực tế

Một công ty sản xuất bánh kẹo cần kiểm soát trọng lượng sản phẩm. Ví dụ tính độ lệch chuẩn cho 5 gói bánh: 48g, 50g, 49g, 51g, 52g.
– Trung bình = 50g
– Phương sai = 2
– Độ lệch chuẩn = √2 ≈ 1.41g

Kết quả cho thấy sai số trọng lượng khoảng 1.41g so với tiêu chuẩn, giúp bộ phận sản xuất điều chỉnh quy trình cho phù hợp.

Ứng dụng của phương sai và độ lệch chuẩn trong phân tích dữ liệu

Xem thêm : Chi tiết công thức tính trung bình cộng và hướng dẫn các bài tập ứng dụng cơ bản

Phương sai và độ lệch chuẩn là hai công cụ thống kê quan trọng giúp đánh giá mức độ phân tán của dữ liệu. Khi phân tích một tập dữ liệu, việc nắm rõ công thức tính độ lệch chuẩn và phương sai sẽ giúp ta hiểu được độ biến thiên và tính ổn định của số liệu.

Trong thực tế, các nhà nghiên cứu thường sử dụng độ lệch chuẩn để đánh giá chất lượng sản phẩm trong sản xuất. Ví dụ, một nhà máy sản xuất ốc vít cần kiểm tra độ đồng đều về kích thước của sản phẩm bằng cách đo công thức tính độ dài đoạn thẳng và tính độ lệch chuẩn. Nếu độ lệch chuẩn lớn, điều đó cho thấy sản phẩm không đồng đều về kích thước.

Các trường hợp sử dụng phương sai và độ lệch chuẩn

Trong giáo dục, giáo viên thường dùng phương sai để đánh giá sự phân hóa điểm số của học sinh. Một lớp có điểm trung bình 7.5 nhưng phương sai lớn sẽ cho thấy có sự chênh lệch đáng kể giữa học sinh giỏi và học sinh yếu.

Ý nghĩa độ lệch chuẩn thể hiện rõ trong lĩnh vực tài chính, nơi các nhà đầu tư sử dụng nó để đánh giá rủi ro của danh mục đầu tư. Theo nghiên cứu của Morgan Stanley, các cổ phiếu có độ lệch chuẩn cao thường mang lại lợi nhuận biến động mạnh, phù hợp với nhà đầu tư chấp nhận rủi ro cao.

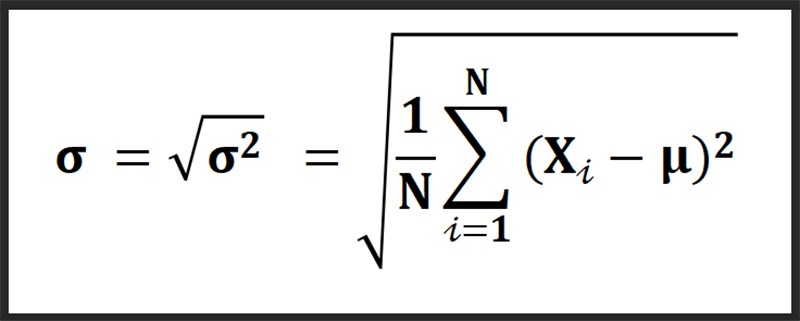
Mối quan hệ giữa phương sai và độ lệch chuẩn

Phương sai và độ lệch chuẩn có mối quan hệ mật thiết với nhau. Độ lệch chuẩn được tính bằng căn bậc hai của phương sai, giúp ta có cái nhìn trực quan hơn về độ phân tán của dữ liệu vì nó có cùng đơn vị đo với dữ liệu gốc.

Giả sử một lớp học có điểm trung bình môn toán là 7.0 và phương sai là 4, khi đó độ lệch chuẩn sẽ là 2 điểm. Điều này có nghĩa là phần lớn điểm số của học sinh sẽ nằm trong khoảng từ 5.0 đến 9.0, tức là lệch trung bình 2 điểm so với giá trị trung bình.

FAQ: Câu hỏi thường gặp về phương sai và độ lệch chuẩn

Với kinh nghiệm hơn 30 năm giảng dạy, tôi nhận thấy học sinh thường gặp nhiều thắc mắc về phương sai và độ lệch chuẩn. Đây là những khái niệm quan trọng trong thống kê mà các em cần nắm vững. Tôi sẽ giải đáp một số câu hỏi phổ biến nhất.

“Thầy ơi, khi nào dùng phương sai và khi nào dùng độ lệch chuẩn ạ?” – đây là câu hỏi mà gần như học sinh nào cũng đặt ra. Phương sai thường được sử dụng để so sánh mức độ phân tán giữa các tập dữ liệu có cùng đơn vị đo. Còn độ lệch chuẩn phù hợp khi muốn đo lường sự phân tán của dữ liệu theo cùng đơn vị với dữ liệu gốc.

Khi tính toán các đại lượng thống kê, việc lựa chọn giữa phương sai và độ lệch chuẩn phụ thuộc vào mục đích sử dụng. Phương sai thích hợp cho các phép tính toán số học và phân tích thống kê chuyên sâu. Độ lệch chuẩn giúp diễn giải kết quả dễ hiểu hơn vì có cùng đơn vị với dữ liệu ban đầu.

Ví dụ trong lớp học của tôi, khi phân tích điểm số của học sinh, tôi thường dùng độ lệch chuẩn để đánh giá mức độ chênh lệch điểm số. Điều này giúp phụ huynh và học sinh dễ dàng hiểu được sự phân hóa về năng lực trong lớp.

Việc áp dụng **công thức tính độ lệch chuẩn và phương sai** đóng vai trò quan trọng trong phân tích dữ liệu thống kê. Hai đại lượng này giúp đánh giá mức độ phân tán của dữ liệu so với giá trị trung bình một cách chính xác và khoa học. Thông qua các ví dụ minh họa cụ thể về cách tính toán và ứng dụng thực tế, các bạn học sinh có thể dễ dàng nắm bắt và vận dụng kiến thức này vào giải quyết các bài toán thống kê cơ bản.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê