Khám phá công thức tính diện tích xung quanh hình trụ và bài tập ứng dụng

Thầy giáo toán với hơn 30 năm kinh nghiệm giảng dạy hướng dẫn chi tiết **công thức tính diện tích xung quanh hình trụ** qua các ví dụ minh họa cụ thể và bài tập thực hành. Phương pháp giải được trình bày đơn giản, dễ hiểu giúp học sinh nắm vững kiến thức hình học không gian cơ bản này.

Công thức tính diện tích xung quanh hình trụ là gì?

Công thức tính diện tích xung quanh của hình trụ là tích của chu vi đáy với chiều cao hình trụ. Nói cách khác, công thức tính diện tích xung quanh hình trụ được biểu diễn bằng công thức:

Bạn đang xem: Khám phá công thức tính diện tích xung quanh hình trụ và bài tập ứng dụng

Sxq = 2πRh

Trong đó R là bán kính đáy và h là chiều cao hình trụ

Để hiểu rõ hơn, bạn có thể hình dung khi trải phẳng phần xung quanh của hình trụ, ta sẽ được một hình chữ nhật có chiều dài bằng chu vi đáy (2πR) và chiều rộng bằng chiều cao hình trụ (h). Diện tích hình chữ nhật này chính là công thức tính diện tích xung quanh của hình trụ.

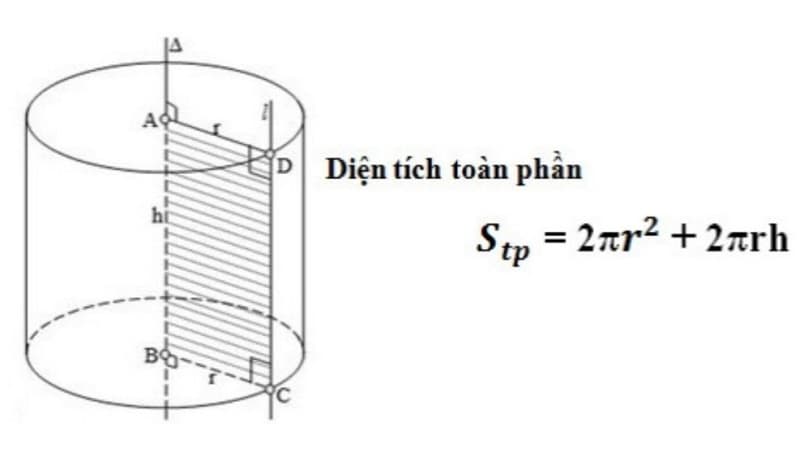
Ví dụ: Một hình trụ có bán kính đáy R = 3cm và chiều cao h = 5cm. Áp dụng công thức, ta có:
Sxq = 2 × 3,14 × 3 × 5 = 94,2 cm². Để tính toàn bộ diện tích hình trụ, bạn cần cộng thêm diện tích hai đáy vào kết quả trên.

Các thành phần cơ bản để tính diện tích xung quanh hình trụ

Để tính chính xác công thức diện tích xung quanh hình trụ, chúng ta cần nắm vững 3 thành phần quan trọng. Mỗi thành phần đóng vai trò thiết yếu trong việc xác định kết quả cuối cùng. Tôi sẽ giải thích chi tiết từng thành phần để các em dễ dàng áp dụng vào bài tập.

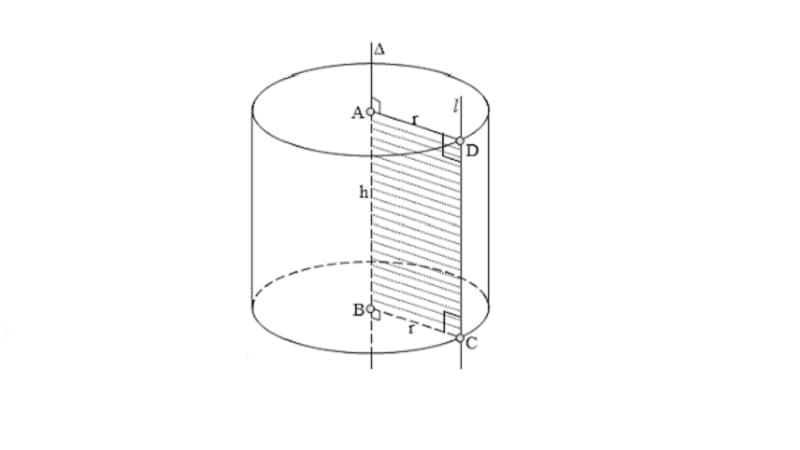
Chiều cao của hình trụ

Chiều cao là khoảng cách vuông góc từ mặt đáy này đến mặt đáy kia của hình trụ. Khi đo chiều cao, các em cần đặt thước vuông góc với mặt đáy để có kết quả chính xác. Giống như việc đo chiều cao của một lon nước ngọt vậy – phải đặt thước thẳng đứng từ đáy lên miệng lon.

Bán kính đáy của hình trụ

Bán kính đáy là độ dài từ tâm đến chu vi của đáy hình trụ. Để tính diện tích hình tròn excel và diện tích xung quanh, bán kính là yếu tố không thể thiếu. Tôi thường ví von bán kính như “cánh tay” của hình tròn – nó vươn ra từ tâm đến mọi điểm trên chu vi.

Số Pi (π) trong công thức

Xem thêm : Lý thuyết công thức thể tích khối lăng trụ và bài tập mẫu có lời giải toán chi tiết

Số Pi là hằng số toán học có giá trị xấp xỉ 3,14. Trong các bài toán thực hành, chúng ta thường lấy π = 3,14 để tính toán cho đơn giản. Số Pi xuất hiện trong công thức vì nó liên quan đến chu vi của hình tròn. Tôi hay nói vui với học sinh rằng Pi giống như “chìa khóa vạn năng” để mở cánh cửa hình tròn vậy.

Phương pháp tính diện tích xung quanh hình trụ chi tiết

Diện tích xung quanh hình trụ là phần diện tích của mặt cong bao quanh thân hình trụ, không bao gồm hai mặt đáy. Để tính được diện tích này một cách chính xác, ta cần nắm vững công thức và các bước thực hiện.

Công thức tổng quát Sxq = 2πrh

Cách tính diện tích xung quanh hình trụ dựa trên công thức

Sxq = 2πrh

Trong đó:
– r là bán kính đáy hình trụ
– h là chiều cao hình trụ
– π ≈ 3,14

Các bước tính diện tích xung quanh hình trụ

Để áp dụng công thức tính diện tích hình trụ đơn giản, ta cần thực hiện theo trình tự các bước sau. Mỗi bước đều quan trọng và cần được thực hiện cẩn thận để có kết quả chính xác.

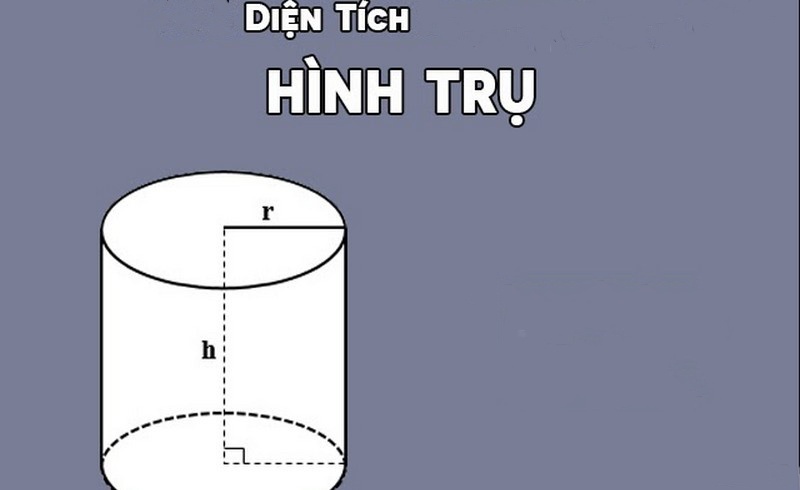
Bước 1: Xác định các thành phần trong công thức

Trước tiên, ta cần xác định chính xác các yếu tố sau:
– Đo hoặc lấy số liệu bán kính đáy (r)
– Đo hoặc lấy số liệu chiều cao (h)
– Sử dụng π = 3,14 cho các bài toán thông thường

Bước 2: Thay số và tính toán

Sau khi có đầy đủ các số liệu, ta thực hiện:
– Nhân 2 với π (3,14)
– Nhân tiếp với bán kính r
– Nhân kết quả với chiều cao h
– Kết quả cuối cùng là diện tích xung quanh hình trụ

Ví dụ minh họa có lời giải chi tiết

Một hình trụ có bán kính đáy r = 5cm và chiều cao h = 10cm. Tính diện tích xung quanh của hình trụ.

Lời giải:
Sxq = 2πrh
= 2 × 3,14 × 5 × 10
= 314 (cm²)

Ngoài diện tích xung quanh, bạn có thể tham khảo thêm công thức tính thể tích hình trụ để giải quyết các bài toán phức tạp hơn về hình trụ.

Các dạng bài tập thường gặp về diện tích xung quanh hình trụ

Khi giải các bài tập diện tích xung quanh hình trụ, việc nắm vững công thức và phương pháp giải là rất quan trọng. Trước khi đi vào chi tiết từng dạng bài, các em cần nhớ công thức diện tích toàn phần hình trụ để áp dụng hiệu quả.

Bài tập tính diện tích xung quanh khi biết bán kính và chiều cao

Xem thêm : Tìm hiểu công thức tính diện tích mặt cầu và bài tập ví dụ chi tiết

Tính diện tích xung quanh hình trụ khi biết bán kính là dạng bài cơ bản nhất. Với công thức Sxq = 2πrh, các em chỉ cần thay số và tính toán. Ví dụ: Cho hình trụ có bán kính r = 3cm và chiều cao h = 5cm. Ta có Sxq = 2 × 3,14 × 3 × 5 = 94,2 cm2.

Bài tập tìm chiều cao khi biết diện tích xung quanh và bán kính

Dạng bài này yêu cầu biến đổi công thức Sxq = 2πrh thành h = Sxq/(2πr). Ví dụ: Hình trụ có diện tích xung quanh 120cm2, bán kính 4cm. Khi đó h = 120/(2 × 3,14 × 4) = 4,78cm.

Bài tập tìm bán kính khi biết diện tích xung quanh và chiều cao

Tương tự như tìm chiều cao, ta biến đổi công thức thành r = Sxq/(2πh). Ví dụ: Hình trụ có diện tích xung quanh 150cm2, chiều cao 6cm. Ta có r = 150/(2 × 3,14 × 6) = 3,98cm.

FAQ: Câu hỏi thường gặp về diện tích xung quanh hình trụ

Khi học về hình trụ, nhiều học sinh thường gặp khó khăn trong việc phân biệt và tính toán các yếu tố liên quan đến diện tích. Một số câu hỏi phổ biến sẽ được giải đáp chi tiết để giúp các em nắm vững kiến thức.

Sự khác biệt giữa diện tích xung quanh và diện tích toàn phần hình trụ

Diện tích xung quanh hình trụ có đáy chỉ tính phần diện tích mặt cong bao quanh hình trụ, không bao gồm hai mặt đáy. Trong khi diện tích toàn phần bằng tổng của diện tích xung quanh và diện tích hai mặt đáy. Tương tự như cách tính diện tích xung quanh hình nón, diện tích xung quanh hình trụ được tính bằng tích của chu vi đáy và chiều cao.

Cách phân biệt hình trụ có đáy và không đáy

Diện tích xung quanh hình trụ không đáy là trường hợp đặc biệt khi hình trụ chỉ có mặt cong mà không có một hoặc cả hai mặt đáy. Giống như một ống trụ rỗng, tương tự như diện tích hình cầu nội tiếp trong hình trụ, việc phân biệt này rất quan trọng khi giải các bài toán thực tế.

Mối liên hệ giữa diện tích xung quanh và thể tích hình trụ

Diện tích xung quanh và thể tích hình trụ có mối quan hệ chặt chẽ thông qua bán kính đáy. Khi bán kính đáy tăng, cả diện tích xung quanh và thể tích đều tăng, nhưng với tốc độ khác nhau. Diện tích xung quanh tăng tỷ lệ thuận với bán kính, trong khi thể tích tăng tỷ lệ thuận với bình phương bán kính.

Việc áp dụng **công thức tính diện tích xung quanh hình trụ** đòi hỏi sự chính xác trong từng bước tính toán. Các thành phần cơ bản như bán kính đáy, chiều cao và hằng số π cần được xác định rõ ràng trước khi thực hiện phép tính. Thông qua các ví dụ minh họa và bài tập thực hành, học sinh có thể nắm vững phương pháp tính toán và áp dụng linh hoạt công thức vào các bài toán khác nhau.

Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian