Công thức tính diện tích hình tròn và bài tập mẫu có lời giải chi tiết

Bài toán về **công thức tính diện tích hình tròn** là kiến thức nền tảng quan trọng trong chương trình toán phổ thông. Với cách giải thích chi tiết kèm ví dụ minh họa cụ thể, các em học sinh sẽ dễ dàng nắm vững và vận dụng thành thạo công thức π.r² trong nhiều bài toán thực tế. Bài viết cung cấp phương pháp tính toán đơn giản cùng các công cụ hỗ trợ hiện đại.

Diện tích hình tròn là gì và ý nghĩa trong thực tế?

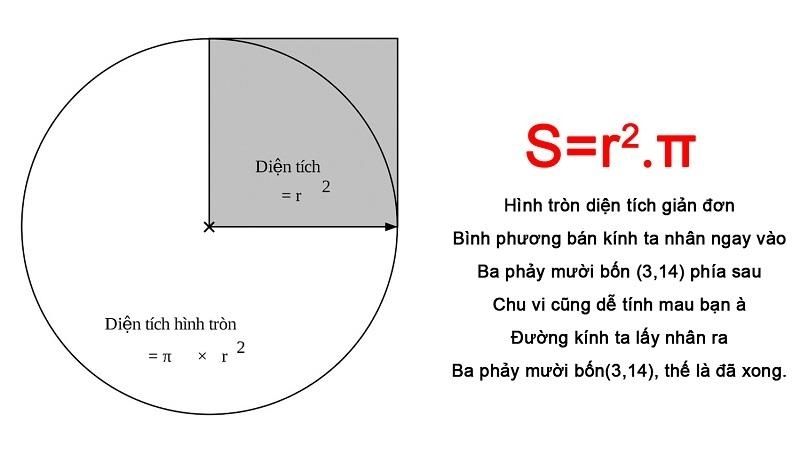
Diện tích hình tròn là gì – đó chính là phần không gian bên trong đường tròn, được tính bằng công thức

Bạn đang xem: Công thức tính diện tích hình tròn và bài tập mẫu có lời giải chi tiết

S = πR²

Trong đó R là bán kính và π ≈ 3,14. Đây là một khái niệm toán học cơ bản nhưng lại có rất nhiều ứng dụng quan trọng trong cuộc sống.

Trong thực tế, việc tính diện tích hình tròn giúp chúng ta giải quyết nhiều bài toán thiết thực. Ví dụ như khi tính diện tích mặt bàn tròn để trải khăn, tính diện tích đáy của các vật dụng hình trụ như lon nước, hay tính diện tích sàn của một căn phòng tròn để lát gạch. Một kiến trúc sư cần nắm vững công thức này để thiết kế các công trình có hình dạng tròn như nhà hát, sân vận động.

Các nhà khoa học cũng thường xuyên áp dụng công thức diện tích hình tròn trong nghiên cứu. Theo Tổ chức Khí tượng Thế giới (WMO), các chuyên gia sử dụng công thức này để tính diện tích vùng ảnh hưởng của bão, từ đó đưa ra cảnh báo chính xác cho người dân. Tương tự, các nhà thiên văn học dùng nó để tính diện tích bề mặt các hành tinh, vệ tinh trong hệ mặt trời.

Công thức tính diện tích hình tròn và các thành phần cơ bản

Công thức tính diện tích hình tròn là

S = π.r²

Xem thêm : Tìm hiểu công thức tính chu vi hình vuông và hướng dẫn giải bài tập từ cơ bản đến nâng cao

Trong đó π (pi) ≈ 3,14 và r là bán kính hình tròn. Đây là công thức cơ bản giúp tính toán diện tích của mọi hình tròn, từ những vật dụng quen thuộc như đĩa ăn đến những công trình kiến trúc lớn. Ngoài ra, để tính toán chính xác hơn, bạn có thể tham khảo thêm cách tính chu vi hình tròn.

Các thành phần trong công thức diện tích hình tròn

Công thức pi r bình phương bao gồm hai thành phần chính. Thứ nhất là hằng số π, một số vô tỉ có giá trị xấp xỉ 3,14 hoặc 22/7. Thành phần thứ hai là bình phương của bán kính r, nghĩa là r nhân với chính nó. Khi biết đường kính D, ta có thể dễ dàng tìm bán kính r bằng cách chia đường kính cho 2.

Cách ghi nhớ và áp dụng công thức π.r²

Để ghi nhớ công thức một cách dễ dàng, tôi thường ví von với học sinh rằng diện tích hình tròn giống như một chiếc bánh pizza. Khi pizza càng to (bán kính lớn), diện tích sẽ tăng lên theo bình phương của bán kính. Điều quan trọng là phải nắm vững đơn vị đo, thường là cm² hoặc m² tùy theo bài toán.

Bài tập mẫu 1: Tính diện tích hình tròn khi biết bán kính

Cho hình tròn có bán kính r = 5cm. Áp dụng công thức S = π.r²:
S = 3,14 × 5² = 3,14 × 25 = 78,5 (cm²)
Vậy diện tích hình tròn là 78,5 cm².

Bài tập mẫu 2: Tính diện tích hình tròn khi biết đường kính

Cho hình tròn có đường kính D = 10m. Ta có:
Bán kính r = D/2 = 10/2 = 5m
S = π.r² = 3,14 × 5² = 3,14 × 25 = 78,5 (m²)

Vậy diện tích hình tròn là 78,5 m².

Hướng dẫn chi tiết cách tính diện tích hình tròn qua các trường hợp

Việc tính diện tích hình tròn là một kỹ năng toán học cơ bản mà ai cũng cần nắm vững. Cách tính diện tích hình tròn phụ thuộc vào các yếu tố đã biết như bán kính, đường kính hoặc chu vi. Với mỗi trường hợp, chúng ta sẽ áp dụng các công thức khác nhau để tìm ra diện tích hình tròn công thức phù hợp nhất.

Tính diện tích hình tròn khi biết bán kính

Khi biết bán kính (R), diện tích hình tròn được tính theo công thức: S = πR². Trong đó π ≈ 3,14. Ví dụ với hình tròn có bán kính 5cm, ta có:

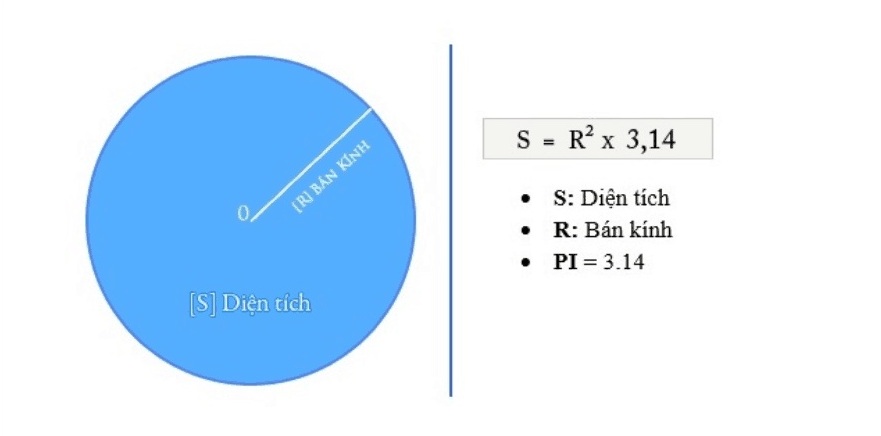
S = 3,14 × 5² = 3,14 × 25 = 78,5 cm²

Tính diện tích hình tròn khi biết đường kính

Với đường kính (D) đã cho, ta có thể tính đường kính qua chu vi hoặc sử dụng công thức: S = π(D/2)². Giả sử đường kính là 10cm:
S = 3,14 × (10/2)² = 3,14 × 5² = 78,5 cm²

Tính diện tích hình tròn khi biết chu vi

Từ chu vi (C), ta có thể tìm bán kính theo công thức R = C/2π, sau đó áp dụng công thức diện tích S = πR². Ví dụ với chu vi 31,4cm:
R = 31,4/(2×3,14) = 5cm
S = 3,14 × 5² = 78,5 cm²

Ứng dụng công thức diện tích hình tròn trong chương trình học các cấp

Công thức tính diện tích hình tròn lớp 5 được áp dụng rộng rãi trong nhiều bài toán thực tế. Các em học sinh sẽ bắt đầu làm quen với những bài tập đơn giản như tính diện tích mặt đáy của lon nước, đĩa CD hay bánh pizza. Khi lên diện tích hình tròn lớp 9, các em sẽ gặp những bài toán phức tạp hơn liên quan đến hình tròn kết hợp với diện tích hình vuông bằng cạnh hay cách tính diện tích hình chữ nhật.

Bài tập cơ bản về diện tích hình tròn lớp 5

Ví dụ 1: Một chiếc đĩa CD có bán kính 6cm. Tính diện tích mặt đĩa CD.
Giải:
– Diện tích hình tròn = π × r²
– Thay số: S = 3,14 × 6² = 3,14 × 36 = 113,04 cm²

Ví dụ 2: Một chiếc bánh pizza có đường kính 30cm. Tính diện tích mặt bánh.

Giải:
– Bán kính r = đường kính/2 = 30/2 = 15cm
– Diện tích S = π × 15² = 3,14 × 225 = 706,5 cm²

Bài tập nâng cao về diện tích hình tròn lớp 9

Ví dụ 1: Cho hình vuông cạnh 10cm. Tính diện tích phần còn lại của hình vuông sau khi cắt bỏ một phần tư hình tròn nội tiếp hình vuông đó.
Giải:
– Diện tích hình vuông: S₁ = 10² = 100cm²
– Bán kính hình tròn bằng nửa cạnh hình vuông: r = 5cm
– Diện tích phần tư hình tròn: S₂ = (π × r²)/4 = (3,14 × 25)/4 = 19,625cm²
– Diện tích phần còn lại: S = S₁ – S₂ = 100 – 19,625 = 80,375cm²

Ví dụ 2: Cho hình tròn bán kính 8cm. Tính diện tích phần hình tròn nằm ngoài hình vuông nội tiếp.
Giải:
– Diện tích hình tròn: S₁ = π × 8² = 3,14 × 64 = 200,96cm²
– Cạnh hình vuông nội tiếp: a = 8√2cm
– Diện tích hình vuông: S₂ = (8√2)² = 128cm²
– Diện tích phần cần tính: S = S₁ – S₂ = 200,96 – 128 = 72,96cm²

Các công cụ hỗ trợ tính diện tích hình tròn hiện đại

Xem thêm : Tổng hợp công thức đường trung tuyến và cách tính chi tiết trong tam giác cơ bản

Việc tính toán diện tích hình tròn ngày nay trở nên dễ dàng hơn rất nhiều nhờ các công cụ công nghệ. Với sự phát triển của internet và thiết bị điện tử, học sinh có thể tiếp cận nhiều phương pháp tính nhanh chóng và chính xác.

Một trong những công cụ phổ biến là các website tính diện tích hình tròn online. Các trang web này chỉ yêu cầu nhập bán kính hoặc đường kính, sau đó tự động tính toán kết quả ngay lập tức. Điều này giúp tiết kiệm thời gian và tránh sai sót khi tính toán thủ công.

Đối với những bạn thường xuyên làm việc với bảng tính, diện tích hình tròn excel có thể được tính nhanh chóng bằng công thức =PI()*R^2, với R là bán kính. Excel còn cho phép tạo các công thức phức tạp hơn để tính công thức diện tích toàn phần hình trụ hoặc tính diện tích hình cầu đơn giản.

Máy tính khoa học cũng là công cụ không thể thiếu. Với diện tích hình tròn casio, các model phổ biến như fx-570 đều có sẵn hằng số π và các phím chức năng tính lũy thừa, giúp việc tính toán trở nên nhanh gọn. Tôi thường khuyên học sinh nên thực hành nhiều với máy tính casio để làm quen với các phím chức năng quan trọng này.

FAQ: Câu hỏi thường gặp về diện tích hình tròn

Khi học về diện tích hình tròn, nhiều học sinh thường gặp một số thắc mắc phổ biến. Tôi sẽ giải đáp những câu hỏi này một cách đơn giản và dễ hiểu nhất.

Làm thế nào để tính diện tích hình tròn khi không có máy tính?

Khi không có máy tính, bạn có thể làm tròn số π ≈ 3,14 hoặc 22/7. Ví dụ với hình tròn bán kính 5cm, ta có thể tính: S = π × 5² = 3,14 × 25 = 78,5 cm². Hoặc dùng phân số: S = (22/7) × 25 = 78,57 cm². Sai số này hoàn toàn chấp nhận được trong nhiều bài toán thực tế.

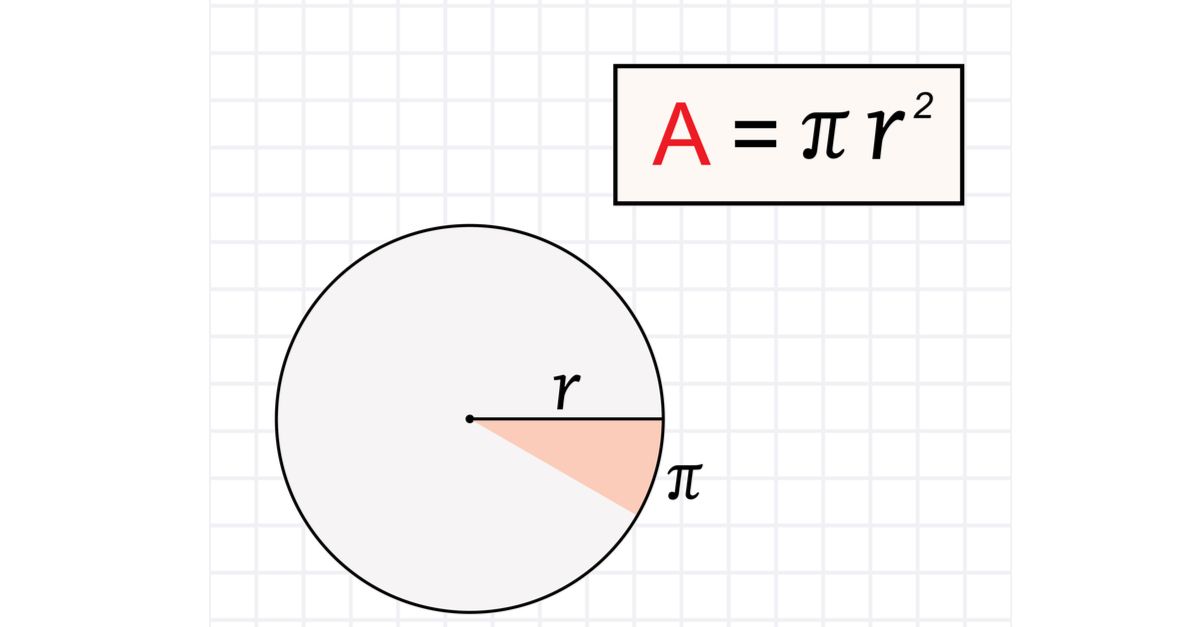
Tại sao công thức diện tích hình tròn lại có số π?

Số π xuất hiện trong công thức diện tích hình tròn vì nó thể hiện mối quan hệ giữa chu vi và đường kính của mọi hình tròn. Khi chia nhỏ hình tròn thành nhiều hình quạt và xếp lại thành hình gần giống hình chữ nhật, chiều cao của hình chữ nhật này bằng bán kính (r) và chiều dài xấp xỉ nửa chu vi (πr), từ đó ta có diện tích πr².

Có thể tính diện tích hình tròn khi chỉ biết chu vi không?

Có thể tính được. Nếu biết chu vi C của hình tròn, ta có thể suy ra bán kính r = C/(2π). Sau đó thay vào công thức S = πr². Ví dụ với chu vi 31,4cm, ta có r = 31,4/(2×3,14) = 5cm, từ đó tính được S = 3,14 × 5² = 78,5 cm².

Việc nắm vững **công thức tính diện tích hình tròn** là nền tảng quan trọng trong học tập toán học. Các phương pháp tính toán đơn giản cùng với những ví dụ minh họa cụ thể giúp học sinh dễ dàng áp dụng công thức π.r² vào thực tế. Những công cụ hỗ trợ hiện đại như máy tính Casio, Excel hay các ứng dụng online đã tạo điều kiện thuận lợi cho việc tính toán nhanh chóng và chính xác.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng