Trang chủ » Công thức tính diện tích hình lập phương và bài tập minh họa

Công thức tính diện tích hình lập phương và bài tập minh họa

Công thức tính diện tích hình lập phương được tổng hợp đầy đủ và chi tiết nhất. Đây là kiến thức quan trọng học sinh cần ghi nhớ để áp dụng vào bài tập hình học không gian.

Có thể bạn quan tâm

Table of Contents

Khái niệm về hình lập phương

Khối hình lập phương gồm có 6 mặt, 8 đỉnh, 12 cạnh. Tất cả các mặt của hình khối này đều là hình vuông bằng nhau, các cạnh bằng nhau. Hay ta có thể hiểu rằng hình lập phương là hình khối có chiều rộng, chiều dài và chiều cao đều bằng nhau.

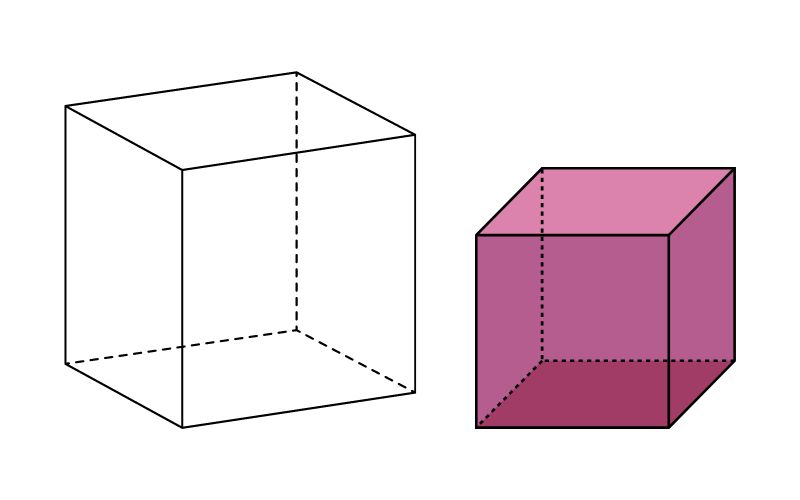
Bạn đang xem: Công thức tính diện tích hình lập phương và bài tập minh họa

Tính chất của hình lập phương bao gồm:

Hình có 6 mặt phẳng và 12 cạnh bằng nhau.
Đường chéo của các mặt bên và của hình khối đều bằng nhau.

Công thức tính diện tích hình lập phương

Diện tích hình lập phương được chia ra thành hai dạng là diện tích xung quanh và diện tích toàn phần. Trong đó, ta có diện tích xung quanh bằng diện tích một mặt nhân với 4 và diện tích toàn phần bằng diện tích một một mặt nhân với 6.

Diện tích xung quanh

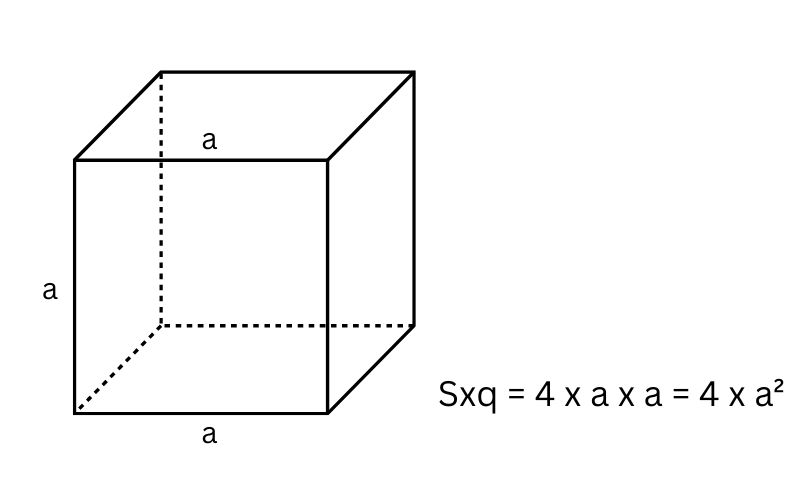
Diện tích xung quanh hình lập phương có cạnh a là tổng diện tích của 4 mặt bên hình lập phương. Như vậy, để tính được diện tích xung quanh, ta lấy bình phương của một cạnh nhân với 4.

Công thức cụ thể như sau: Sxq = 4 x a²

Trong đó:

Sxq: Diện tích xung quanh.
a: Các cạnh của một hình lập phương.

công thức tính diện tích hình lập phương — Công thức tính diện tích xung quanh hình lập phương

Diện tích toàn phần

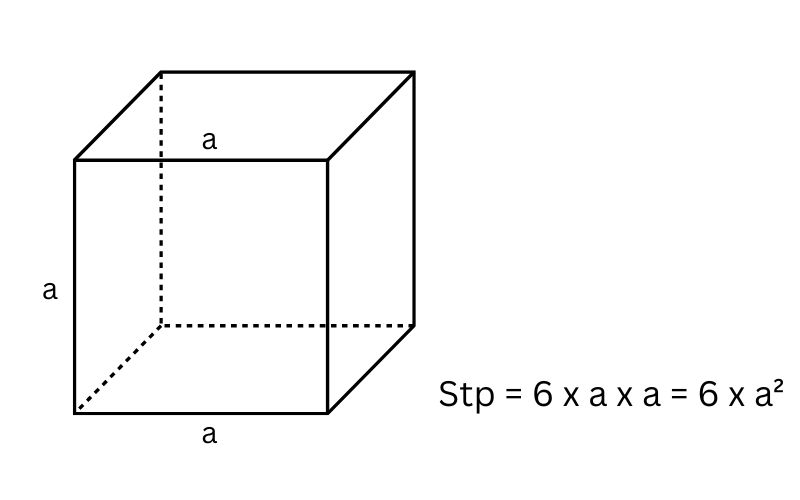
Diện tích toàn phần của hình lập phương có cạnh a là tổng diện tích xung quanh hình và 2 mặt còn lại. Theo đó, muốn tính diện tích xung quanh của hình lập phương, ta lấy bình phương của một cạnh nhân với 6.

Công thức cụ thể như sau: Stp = 6 x a²

Trong đó:

Stp: Diện tích toàn phần.
a: Các cạnh của một hình lập phương.

công thức diện tích toàn phần hình lập phương — Công thức tính diện tích toàn phần hình lập phương

Bài tập ứng dụng công thức tính diện tích

Tổng hợp bài tập có áp dụng công thức diện tích của hình bình hành cho học sinh tham khảo. Trong các dạng bài tập và bài kiểm tra, giáo viên thường cho nhiều bài toán tính diện tích được gây nhiễu cho học sinh. Do đó khi làm bài bạn cần đọc kỹ đề và quy đổi về cùng một đơn vị diện tích khi thực hiện các phép tính.

Bài tập

Một số bài tập minh họa bao gồm:

Xem thêm : Công thức tính diện tích xung quanh hình nón và bài tập hướng dẫn chi tiết

Bài 1: Cho hình lập phương A có diện tích toàn phần là 320cm². Tính độ dài cạnh của hình lập phương đó.

Bài 2: Cho hình lập phương với lần lượt kích thước cạnh là 4cm. Tính diện tích xung quanh và diện tích toàn phần của hình lập phương đó.

Bài 3: Cho hình lập phương ABCD.EFGH có độ dài các cạnh bằng nhau, biết diện tích toàn phần hình lập phương là 54cm². Tính độ dài các cạnh có trong hình lập phương đó.

Bài 4: Người ta xếp một số viên gạch có dạng hình hộp chữ nhật tạo thành khối gạch hình lập phương có cạnh dài 20cm. Tính diện tích xung quanh và diện tích toàn phần của khối gạch hình lập phương trên.

Bài 5: Sắp xếp một số viên gạch thành hình khối lập phương với cạnh dài 15cm. Tính diện tích xung quanh và toàn phần khối lập phương. Hỏi kích thước viên gạch là bao nhiêu?

Đáp án

Đáp án và cách giải tham khảo cho các bài tập ứng dụng bao gồm:

Bài 1: Ta có diện tích một mặt của hình lập phương là: 150 : 6 = 25cm².

Vậy độ dài cạnh của hình lập phương là: 25 : 5 = 5cm.

Bài 2: Diện tích xung quanh là: Sxq = 4 x a² = 4 x 4² = 64m².

Diện tích toàn phần là Stp = 6 x a² = 6 x 4² = 96m².

⇒ Sxq = 64cm² và Stp = 96m².

Bài 3: Gọi a là độ dài của một hình lập phương.

Xem thêm : Tìm hiểu công thức tính diện tích mặt cầu và bài tập ví dụ chi tiết

⇔ Stp = 6 x a x a

⇔ 54 = 6 x a x a

⇔ a x a = 54/6

⇔ a x a = 9

⇒ a = 3

Vậy chiều dài các cạnh của hình lập phương ABCD.EFGH là 3cm.

Bài 4: Diện tích xung quanh khối gạch: Sxq = 4 x a x a = 4 x 20 x 20 = 1600cm².

Diện tích toàn phần khối gạch: Stp = 6 x a x a = 6 x 20 x 20 = 2400 cm².

Vậy Sxq là 1600cm² và Stp là 2400 cm².

Bài 5: Diện tích Sxq = 4 x a x a = 4 x 15 x 15 = 900cm²

Diện tích toàn phần Stp = 6 x a x a = 6 x 15 x 15 = 1250cm²

Vì là hình lập phương cạnh 15cm nên chiều dài (a) = chiều rộng (a) = chiều cao (a) của viên gạch. Từ đó suy ra viên gạch có chiều dài là 15cm.

Kết luận

Công thức tính diện tích hình lập phương là phần nội dung kiến thức trọng tâm liên quan đến nhiều dạng bài tập. Hy vọng những thông tin được cập nhật sẽ giúp học sinh cần nắm vững thông tin này trong chương trình học.

Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian