Tìm hiểu công thức tính chu vi hình vuông và hướng dẫn giải bài tập từ cơ bản đến nâng cao

Chúng ta áp dụng **công thức tính chu vi hình vuông** mỗi ngày trong cuộc sống mà không hề hay biết. Bài viết này trình bày chi tiết công thức, các bước tính toán và giải thích cặn kẽ những ví dụ thực tế giúp các em nắm vững kiến thức cơ bản này một cách dễ dàng và thú vị.

Chu vi hình vuông là gì và tầm quan trọng trong học tập toán học?

Chu vi hình vuông là gì – đó là tổng độ dài của 4 cạnh bằng nhau tạo nên hình vuông. Với đặc điểm 4 cạnh bằng nhau và 4 góc vuông, việc tính chu vi hình vuông trở nên đơn giản hơn nhiều so với các hình khác. Chỉ cần biết độ dài một cạnh, ta có thể dễ dàng tính được chu vi bằng cách nhân với 4.

Bạn đang xem: Tìm hiểu công thức tính chu vi hình vuông và hướng dẫn giải bài tập từ cơ bản đến nâng cao

Hiểu được cách tính chu vi hình vuông sẽ giúp học sinh nắm vững kiến thức cơ bản về hình học phẳng. Đây là nền tảng quan trọng để tiếp cận các bài toán phức tạp hơn về diện tích và thể tích. Ví dụ khi học về công thức tính diện tích hình vuông, việc nắm chắc chu vi sẽ giúp học sinh dễ dàng liên hệ và ghi nhớ công thức.

Trong thực tế, chu vi hình vuông được ứng dụng rộng rãi trong nhiều lĩnh vực như xây dựng, kiến trúc hay thiết kế. Một kiến trúc sư cần tính chu vi sân vườn hình vuông để lắp đặt hàng rào. Một nhà thiết kế nội thất cần biết chu vi để trang trí viền gương, khung tranh. Những ví dụ thực tế này giúp học sinh thấy được tính ứng dụng và tầm quan trọng của kiến thức toán học trong cuộc sống.

Công thức tính chu vi hình vuông và các thành phần cơ bản

Hình vuông là một trong những hình học cơ bản nhất mà ai cũng cần nắm vững. Việc tính công thức chu vi hình vuông đơn giản hơn nhiều so với công thức tính chu vi hình chữ nhật do các cạnh bằng nhau.

Các yếu tố cần biết khi tính chu vi hình vuông

Để tính được chu vi hình vuông, chỉ cần biết độ dài một cạnh của hình vuông là đủ. Điều đặc biệt của hình vuông là có 4 cạnh bằng nhau và 4 góc vuông bằng 90 độ. Công thức tính chu vi hình vuông sẽ dựa trên đặc điểm này.

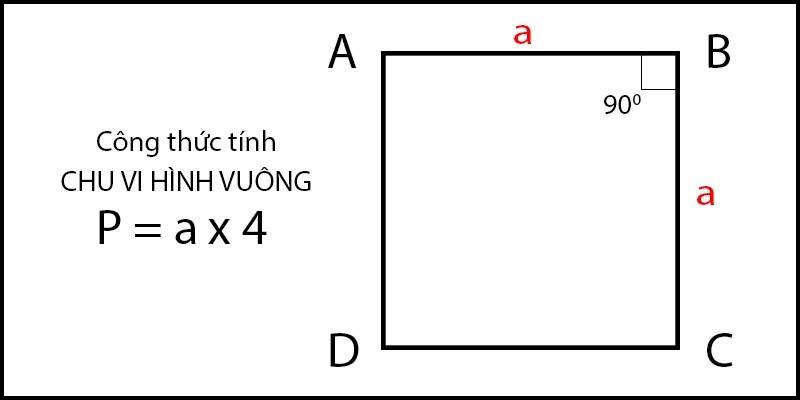
Công thức tính chu vi hình vuông cơ bản P = 4a

Với P là chu vi hình vuông và a là độ dài cạnh, ta có chu vi hình vuông cơ bản được tính bằng công thức

P = 4a

Công thức này áp dụng cho mọi hình vuông, không phụ thuộc vào kích thước lớn hay nhỏ.

Giải thích ý nghĩa của công thức

Xem thêm : Công thức tính diện tích parabol và hướng dẫn cách giải chi tiết nhất

Công thức P = 4a có ý nghĩa rất đơn giản: chu vi hình vuông bằng tổng độ dài 4 cạnh. Do các cạnh bằng nhau nên chỉ cần nhân độ dài một cạnh với 4. Ví dụ khi một cạnh dài 5cm, chu vi sẽ là 20cm.

Bài tập mẫu áp dụng công thức cơ bản

Bài toán: Một hình vuông có cạnh 8cm, tính chu vi hình vuông.
Giải:
– Áp dụng công thức P = 4a
– Thay a = 8cm
– P = 4 × 8 = 32cm
Vậy chu vi hình vuông là 32cm.

Hướng dẫn các bước tính chu vi hình vuông đơn giản và chính xác

Việc tính chu vi hình vuông đơn giản luôn là kiến thức cơ bản quan trọng mà học sinh cần nắm vững. Với đặc điểm 4 cạnh bằng nhau, hình vuông giúp việc tính toán chu vi trở nên dễ dàng và nhanh chóng.

Quy trình 3 bước tính chu vi hình vuông

Bước 1: Xác định độ dài cạnh của hình vuông. Đo chính xác độ dài một cạnh bằng thước kẻ hoặc lấy số liệu từ đề bài.

Bước 2: Áp dụng công thức chu vi hình vuông = 4 × cạnh. Công thức này dựa trên tính chất 4 cạnh bằng nhau của hình vuông.

Bước 3: Thực hiện phép nhân và ghi kết quả kèm đơn vị đo. Với học sinh lớp 4, lớp 5, việc kiểm tra lại kết quả rất cần thiết để tránh sai sót.

Ví dụ minh họa chi tiết từng bước

Một hình vuông có cạnh 5cm, tính chu vi hình vuông như thế nào? Ta áp dụng từng bước:
– Cạnh a = 5cm
– Chu vi = 4 × 5 = 20cm

Ngoài ra, khi học về hình vuông, các em có thể tham khảo thêm công thức tính đường chéo hình vuông để hiểu sâu hơn về tính chất của hình vuông.

• Ví dụ và lời giải chi tiết

Bài 1: Một mảnh vườn hình vuông có cạnh 12m. Tính chu vi mảnh vườn.
Lời giải:
– Cạnh mảnh vườn = 12m
– Chu vi = 4 × 12 = 48m
– Đáp số: 48m

Bài 2: Một bức tranh hình vuông có chu vi 36cm. Tính độ dài cạnh của bức tranh.
Lời giải:
– Gọi cạnh bức tranh là a
– Ta có: 4 × a = 36
– Suy ra: a = 36 ÷ 4 = 9
– Đáp số: 9cm

Các dạng bài tập thường gặp về chu vi hình vuông

Khi học về hình vuông, việc nắm vững các dạng bài tập về chu vi sẽ giúp học sinh áp dụng tốt vào thực tế. Tôi sẽ phân tích chi tiết từng dạng bài tập phổ biến để các em dễ dàng tiếp thu.

Tính chu vi hình vuông khi biết cạnh

Đây là dạng bài tập cơ bản nhất về chu vi hình vuông cạnh a. Với đặc điểm 4 cạnh bằng nhau, ta chỉ cần nhân độ dài cạnh với 4 là ra kết quả. Nhiều học sinh thường nhầm lẫn giữa chu vi và diện tích, vì vậy cần phân biệt rõ chu vi là tổng độ dài các cạnh.

Tính cạnh hình vuông khi biết chu vi

Ngược lại với dạng trên, khi biết chu vi ta có thể tìm được công thức tính cạnh hình vuông bằng cách chia chu vi cho 4. Tương tự như việc tính công thức tính chu vi tam giác vuông, ta cần xác định rõ mối quan hệ giữa các yếu tố.

Bài toán thực tế liên quan đến chu vi hình vuông

Xem thêm : Tìm hiểu công thức tính bán kính đường tròn ngoại tiếp và bài tập áp dụng chi tiết

Trong cuộc sống, ta thường gặp nhiều bài toán liên quan đến chu vi hình vuông như tính chiều dài hàng rào, độ dài viền khăn… Tương tự như công thức tính chu vi hình thang, việc áp dụng công thức vào thực tế giúp giải quyết nhiều vấn đề thiết thực.

Ví dụ và lời giải chi tiết

Bài 1: Một mảnh vườn hình vuông có cạnh 25m. Tính chi phí làm hàng rào xung quanh, biết 1m hàng rào có giá 150.000đ.

Lời giải:
– Chu vi mảnh vườn = 25 × 4 = 100m
– Chi phí = 100 × 150.000 = 15.000.000đ

Bài 2: Một sân chơi hình vuông có chu vi 120m. Tính độ dài mỗi cạnh của sân.

Lời giải:
– Độ dài mỗi cạnh = 120 ÷ 4 = 30m

FAQ: Câu hỏi thường gặp về chu vi hình vuông

Khi học về hình vuông, nhiều học sinh thường gặp các thắc mắc về cách tính và ý nghĩa của chu vi. Những câu hỏi phổ biến sẽ được giải đáp chi tiết để giúp các em nắm vững kiến thức cơ bản này.

Làm sao để nhớ công thức chu vi hình vuông dễ dàng?

Để nhớ chu vi hình vuông bằng bao nhiêu, em có thể tưởng tượng việc đi bộ quanh một hình vuông. Khi đi từ điểm xuất phát, em sẽ đi qua 4 cạnh bằng nhau và quay về điểm ban đầu. Vì vậy, tổng quãng đường đi chính là chu vi, bằng 4 lần độ dài một cạnh. Công thức chu vi hình vuông đơn giản P = 4a (với a là độ dài cạnh) sẽ dễ nhớ hơn khi gắn với hình ảnh thực tế này.

Tại sao chu vi hình vuông bằng 4 lần cạnh?

Tính chất đặc biệt của hình vuông là có 4 cạnh bằng nhau. Khi tính tổng độ dài các cạnh để được chu vi, ta cộng 4 cạnh có độ dài giống nhau. Giống như việc tính tổng tiền khi mua 4 quyển vở cùng giá, ta chỉ cần nhân giá một quyển với 4. Tương tự như công thức tính chu vi đường tròn, công thức chu vi hình vuông cũng phản ánh đặc điểm hình học của nó.

Mối liên hệ giữa chu vi và diện tích hình vuông?

Chu vi và diện tích hình vuông có mối quan hệ mật thiết thông qua độ dài cạnh. Nếu biết chu vi, ta có thể tìm được độ dài cạnh bằng cách chia chu vi cho 4. Từ độ dài cạnh này, ta bình phương nó lên sẽ được diện tích. Ngược lại, khi biết diện tích, lấy căn bậc hai ta được độ dài cạnh, nhân với 4 sẽ ra chu vi.

Việc áp dụng **công thức tính chu vi hình vuông** là kỹ năng toán học cơ bản mà mọi học sinh cần nắm vững. Với công thức đơn giản P = 4a và các bước thực hiện rõ ràng, các em có thể tự tin giải quyết nhiều dạng bài tập từ cơ bản đến nâng cao. Thông qua các ví dụ minh họa và bài tập thực tế, kiến thức về chu vi hình vuông trở nên gần gũi và dễ áp dụng trong cuộc sống hàng ngày.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng