Lý thuyết công thức tính bán kính hình tròn và bài tập mẫu chi tiết

Thầy giáo chia sẻ các **công thức tính bán kính hình tròn** thông qua phương pháp giảng dạy đơn giản, dễ hiểu. Bài viết trình bày chi tiết cách tính bán kính từ chu vi, diện tích và các trường hợp đường tròn nội ngoại tiếp tam giác kèm ví dụ minh họa cụ thể. Kiến thức cơ bản này giúp học sinh nắm vững và vận dụng hiệu quả vào giải toán hình học.

Bán kính hình tròn là gì và tầm quan trọng của nó trong hình học?

Bán kính hình tròn là đoạn thẳng nối từ tâm đến một điểm bất kỳ trên đường tròn. Nó là một trong những yếu tố quan trọng nhất để xác định kích thước và các tính chất của hình tròn. Tôi thường ví von bán kính như “cánh tay” của hình tròn – nó vươn ra đều đặn từ tâm để tạo nên một hình tròn hoàn hảo.

Bạn đang xem: Lý thuyết công thức tính bán kính hình tròn và bài tập mẫu chi tiết

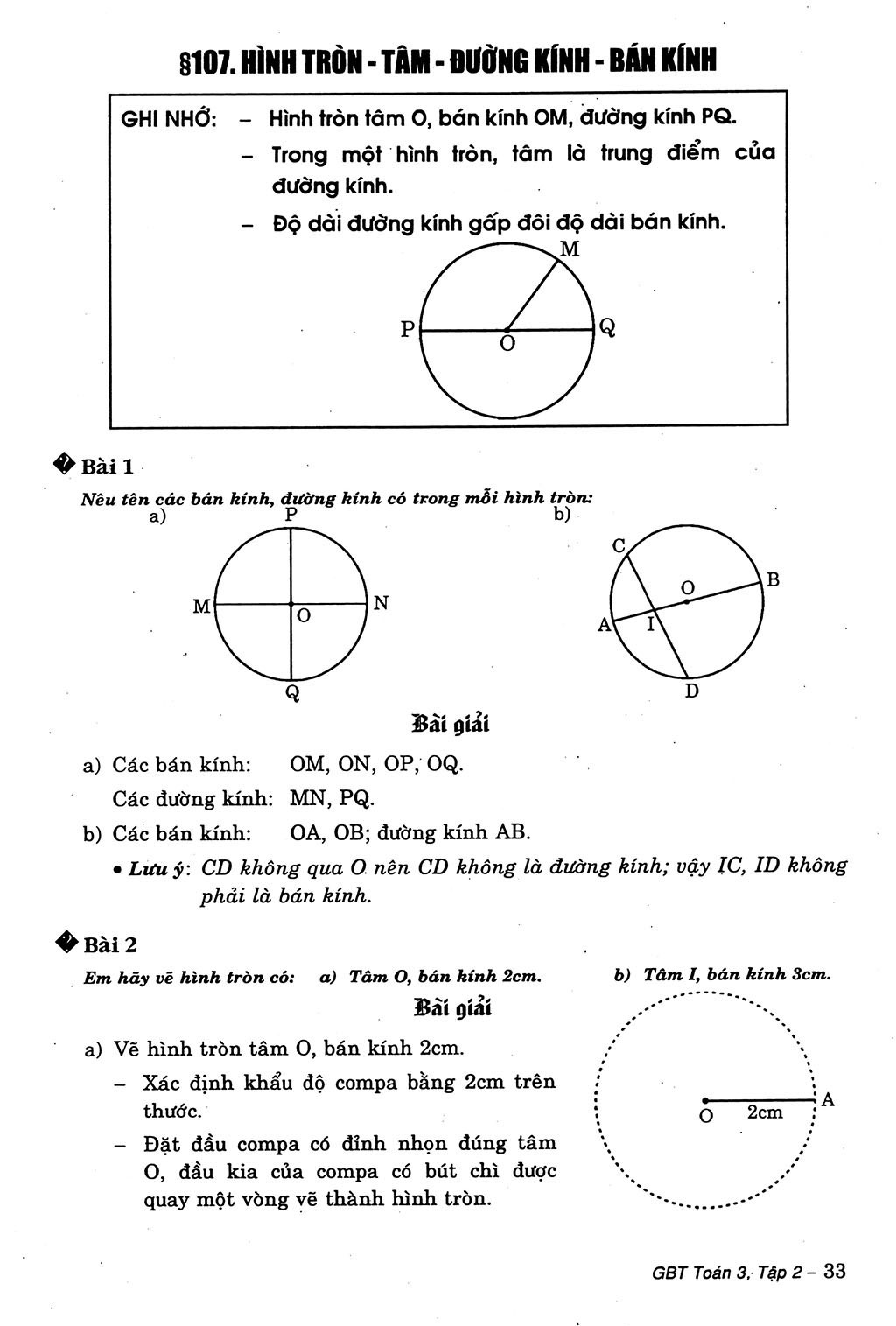
Trong suốt 30 năm giảng dạy, tôi nhận thấy nhiều học sinh gặp khó khăn khi phân biệt bán kính với đường kính. Để dễ nhớ, các em có thể hình dung: nếu đường kính là cả chiếc bánh mì thì bán kính chính là một nửa chiếc bánh đó. Bán kính luôn bằng 1/2 đường kính và ngược lại, đường kính bằng 2 lần bán kính.

Bán kính đóng vai trò then chốt trong việc tính toán các yếu tố của hình tròn như chu vi và diện tích. Ví dụ, với một hình tròn có bán kính R, ta có:
– Chu vi = 2πR
– Diện tích = πR²

Khi giải các bài toán về hình tròn, việc xác định chính xác bán kính là bước đầu tiên và quan trọng nhất. Một sai sót nhỏ trong việc đo bán kính có thể dẫn đến kết quả sai lệch đáng kể khi tính toán các yếu tố khác của hình tròn.

Các công thức tính bán kính hình tròn cơ bản cần nắm vững

Để tính bán kính hình tròn, chúng ta có thể sử dụng mối liên hệ với chu vi hoặc diện tích. Công thức tính bán kính hình tròn sẽ được rút ra từ công thức chu vi đường tròn và cách tính diện tích hình tròn. Việc nắm vững các công thức tính r hình tròn giúp giải quyết nhiều bài toán thực tế.

Công thức tính bán kính từ chu vi đường tròn

Khi biết chu vi đường tròn C, ta có công thức tính bán kính r như sau:

r = C/(2π)

Trong đó:
– r là bán kính cần tìm
– C là chu vi đường tròn
– π ≈ 3,14

Ví dụ minh họa tính bán kính khi biết chu vi

Một đường tròn có chu vi là 31,4cm. Tính bán kính của đường tròn.

Giải:
– Áp dụng công thức r = C/(2π)
– Thay số: r = 31,4/(2 × 3,14) = 5cm
Vậy bán kính của đường tròn là 5cm.

Công thức tính bán kính từ diện tích hình tròn

Khi biết diện tích hình tròn S, ta có công thức tính bán kính r:

Xem thêm : Chi tiết công thức tính chiều cao hình thang và phương pháp xác định chuẩn xác nhất

r = √(S/π)

Trong đó:
– r là bán kính cần tìm
– S là diện tích hình tròn
– π ≈ 3,14

Bài tập mẫu tính bán kính khi biết diện tích

Một hình tròn có diện tích là 78,5cm². Tính bán kính của hình tròn.
Giải:
– Áp dụng công thức r = √(S/π)
– Thay số: r = √(78,5/3,14) = √25 = 5cm
Vậy bán kính của hình tròn là 5cm.

Phương pháp tính bán kính đường tròn nội tiếp và ngoại tiếp

Việc tính toán bán kính đường tròn nội tiếp và ngoại tiếp là một kỹ năng quan trọng trong hình học. Để tính được bán kính đường tròn nội tiếp và bán kính đường tròn ngoại tiếp, chúng ta cần nắm vững công thức tính bán kính đường tròn ngoại tiếp và áp dụng phương trình đường tròn chuẩn tắc một cách linh hoạt.

Công thức tính bán kính đường tròn nội tiếp tam giác

Công thức tính bán kính đường tròn nội tiếp tam giác ABC có độ dài các cạnh lần lượt là a, b, c và diện tích là S được xác định bằng công thức:

r = S/p

Trong đó p là nửa chu vi tam giác (p = (a + b + c)/2). Công thức này giúp ta tính toán chính xác bán kính đường tròn tiếp xúc với cả ba cạnh của tam giác.

Ví dụ tính bán kính đường tròn nội tiếp

Cho tam giác ABC có các cạnh: a = 13cm, b = 14cm, c = 15cm.
Bước 1: Tính nửa chu vi p = (13 + 14 + 15)/2 = 21cm
Bước 2: Tính diện tích S = √(p(p-a)(p-b)(p-c)) = 84cm²
Bước 3: Tính bán kính r = S/p = 84/21 = 4cm

Công thức tính bán kính đường tròn ngoại tiếp tam giác

Bán kính đường tròn ngoại tiếp tam giác ABC được tính theo công thức:

R = abc/(4S)

Xem thêm : Tìm hiểu công thức tính khoảng cách từ điểm đến đường thẳng và bài tập áp dụng chi tiết

Với a, b, c là độ dài các cạnh và S là diện tích tam giác. Đây là công thức cơ bản giúp xác định bán kính đường tròn đi qua cả ba đỉnh của tam giác.

Bài tập mẫu tính bán kính đường tròn ngoại tiếp

Cho tam giác ABC có các cạnh: a = 6cm, b = 8cm, c = 10cm.
Bước 1: Tính nửa chu vi p = (6 + 8 + 10)/2 = 12cm
Bước 2: Tính diện tích S = √(12(12-6)(12-8)(12-10)) = 24cm²
Bước 3: Tính bán kính R = (6 × 8 × 10)/(4 × 24) = 5cm

Các phương pháp tìm bán kính hình tròn trong bài toán thực tế

Việc xác định bán kính hình tròn là một kỹ năng quan trọng trong nhiều bài toán thực tế. Cách tính bán kính đường tròn có thể thực hiện qua hai phương pháp chính: đo trực tiếp hoặc tính gián tiếp thông qua các yếu tố khác như tính đường kính qua diện tích và công thức tính độ dài cung tròn.

Phương pháp đo đạc trực tiếp

Cách tìm bán kính hình tròn bằng phương pháp đo đạc trực tiếp thường áp dụng với các vật thể tròn có kích thước vừa phải. Để đo chính xác, ta cần sử dụng thước đo phù hợp như thước kẹp, thước dây hoặc compa. Việc đo từ tâm đến một điểm bất kỳ trên đường tròn sẽ cho ta giá trị bán kính cần tìm.

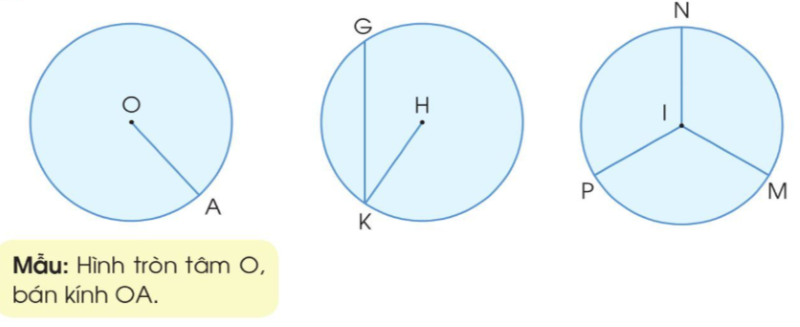
Ví dụ thực hành đo bán kính vật tròn

Giả sử cần đo bán kính một chiếc đĩa tròn. Đầu tiên, xác định tâm đĩa bằng cách vẽ hai đường kính vuông góc. Điểm giao nhau của hai đường kính chính là tâm. Sau đó dùng thước đo từ tâm đến mép đĩa, ta được giá trị bán kính. Để tăng độ chính xác, nên đo nhiều lần ở các vị trí khác nhau và lấy giá trị trung bình.

Phương pháp tính gián tiếp qua các yếu tố khác

Công thức tính bán kính hình tròn có thể được suy ra từ các yếu tố đã biết như chu vi, diện tích hoặc độ dài cung. Phương pháp này đặc biệt hữu ích khi không thể đo trực tiếp hoặc cần độ chính xác cao trong các bài toán kỹ thuật và khoa học.

Bài tập thực tế về tính bán kính

Một ví dụ điển hình là bài toán tính bán kính bể chứa nước hình trụ tròn. Biết diện tích đáy bể là 78,5m². Áp dụng công thức S = πr², ta có:
78,5 = 3,14 × r²
r = √(78,5/3,14) = 5m
Kết quả cho thấy bể chứa có bán kính 5m.

FAQ: Câu hỏi thường gặp về cách tính bán kính hình tròn

Khi học về hình tròn, nhiều bạn học sinh thường gặp khó khăn trong việc tính toán bán kính. Tôi sẽ giải đáp một số câu hỏi phổ biến về vấn đề này dựa trên kinh nghiệm 30 năm giảng dạy của mình.

Q1: Làm thế nào để tính bán kính từ chu vi hình tròn?
A1: Công thức đơn giản là R = C/2π, trong đó C là chu vi và π ≈ 3,14. Ví dụ với chu vi 31,4cm, bán kính sẽ là 31,4/(2×3,14) = 5cm.

Q2: Có cách nào dễ nhớ để tính bán kính từ diện tích không?
A2: Từ công thức S = πR², ta có R = √(S/π). Giả sử diện tích là 78,5cm², bán kính sẽ là √(78,5/3,14) = 5cm.

Q3: Làm sao để cách tính bán kính đường tròn nội ngoại tiếp tam giác?
A3: Với đường tròn nội tiếp, bán kính = Diện tích tam giác/(nửa chu vi). Với đường tròn ngoại tiếp, bán kính = (a×b×c)/(4×Diện tích tam giác), trong đó a, b, c là độ dài các cạnh.

Q4: Có mẹo nào để kiểm tra kết quả tính bán kính?
A4: Thay số vào công thức diện tích S = πR² hoặc chu vi C = 2πR để kiểm chứng. Nếu kết quả phù hợp với dữ kiện ban đầu thì bán kính tính đúng.

Việc nắm vững các **công thức tính bán kính hình tròn** giúp học sinh giải quyết nhiều dạng toán từ cơ bản đến nâng cao. Các công thức tính bán kính từ chu vi, diện tích và trong trường hợp đường tròn nội ngoại tiếp đều có mối liên hệ chặt chẽ với nhau. Thông qua các ví dụ minh họa và bài tập thực tế, người học dễ dàng vận dụng kiến thức vào cuộc sống hàng ngày.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng