Tìm hiểu chi tiết công thức tích có hướng kèm bài tập và lời giải chi tiết

Phép tính **công thức tích có hướng** đóng vai trò quan trọng trong việc xác định diện tích, thể tích và các đại lượng vật lý. Bài viết trình bày chi tiết các công thức, tính chất cùng nhiều ví dụ minh họa giúp các em dễ dàng nắm vững kiến thức này. Đặc biệt phân tích rõ sự khác biệt giữa tích có hướng và tích vô hướng trong toán học.

Tích có hướng là gì và ý nghĩa trong toán học?

Khi học toán, các em thường gặp khó khăn với khái niệm tích có hướng là gì. Thầy sẽ giải thích đơn giản: Tích có hướng là phép nhân hai đại lượng vectơ để tạo ra một đại lượng mới, kết quả có thể là một số vô hướng hoặc một vectơ, tùy thuộc vào cách thực hiện phép nhân.

Bạn đang xem: Tìm hiểu chi tiết công thức tích có hướng kèm bài tập và lời giải chi tiết

Để dễ hình dung, các em có thể tưởng tượng như khi đẩy một chiếc xe. Lực đẩy của em (vectơ thứ nhất) tác động lên xe (vectơ thứ hai) sẽ tạo ra một kết quả – đó chính là sự chuyển động của xe theo một hướng nhất định. Tích có hướng trong toán học giúp ta mô tả chính xác mối quan hệ này.

Trong thực tế, tích có hướng được ứng dụng rộng rãi trong vật lý và kỹ thuật. Ví dụ, khi tính moment lực trong cơ học, ta cần dùng tích có hướng giữa vectơ lực và vectơ khoảng cách từ điểm tác dụng lực đến trục quay. Giáo sư Stephen Hawking từng nhấn mạnh tầm quan trọng của tích có hướng trong việc mô tả chuyển động của các vật thể trong không gian vũ trụ.

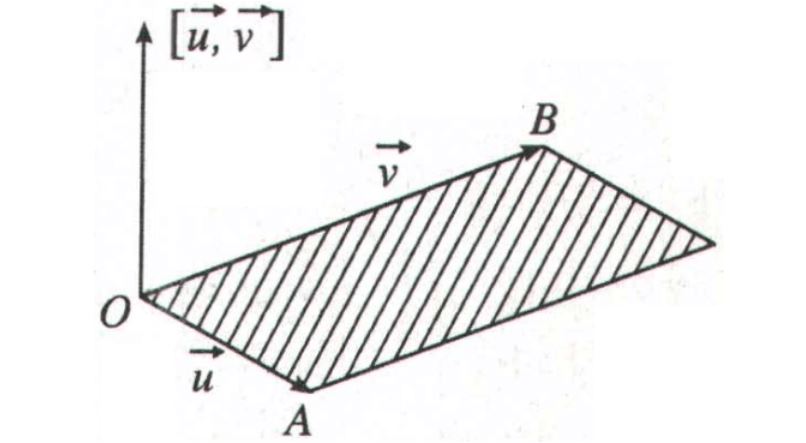
Với các em học sinh yếu toán, thầy khuyên nên bắt đầu bằng cách vẽ hình minh họa và thực hành nhiều bài tập cơ bản. Việc hiểu rõ ý nghĩa hình học sẽ giúp các em nắm vững khái niệm này tốt hơn là chỉ học thuộc công thức máy móc.

Công thức tính tích có hướng của hai vector và ứng dụng

Tích có hướng là phép toán quan trọng giữa hai vector, cho kết quả là một vector vuông góc với cả hai vector ban đầu. Phép toán này có nhiều ứng dụng trong vật lý và các ngành kỹ thuật, đặc biệt khi nghiên cứu chuyển động quay và lực từ trường.

Định nghĩa và công thức tổng quát

Công thức tính tích có hướng của hai vector a và b được xác định bởi:

a × b = |a||b|sin(α)n

Trong đó |a| và |b| là độ dài của hai vector, α là góc giữa chúng và n là vector đơn vị vuông góc với mặt phẳng chứa hai vector theo quy tắc bàn tay phải. Tương tự như cách biểu diễn số phức trong mặt phẳng, tích có hướng của hai vector cũng có thể được biểu diễn bằng các thành phần tọa độ.

Tính chất của tích có hướng

Tích có hướng của hai vector vuông góc có độ lớn bằng tích độ dài của hai vector. Khi hai vector song song, tích có hướng bằng 0. Tính chất phản giao hoán thể hiện qua công thức:

a × b = -(b × a)

Xem thêm : Công thức tính góc giữa hai đường thẳng kèm bài tập minh họa

Điều đặc biệt là tích có hướng không tuân theo tính chất kết hợp như phép nhân thông thường.

Ví dụ minh họa cách tính tích có hướng

Giả sử có vector a = (3,0,0) và b = (0,4,0). Áp dụng công thức tính theo định thức, ta có: a × b = (0,0,12). Vector kết quả vuông góc với cả a và b, có độ lớn bằng 12 đơn vị.

Bài tập 1: Tính tích có hướng của hai vector vuông góc

Cho vector p = (2,0,0) và q = (0,3,0). Ta thấy hai vector vuông góc với nhau nên sin(90°) = 1. Độ lớn của tích có hướng sẽ là |p||q| = 2×3 = 6. Vector kết quả là (0,0,6).

Bài tập 2: Tính tích có hướng khi biết góc giữa hai vector

Cho vector m = (1,1,0) và n = (1,0,0) với góc giữa chúng là 45°. Áp dụng công thức |m||n|sin(45°), ta có độ lớn của tích có hướng là √2 × 1 × 1/√2 = 1. Vector kết quả có hướng vuông góc với mặt phẳng chứa m và n.

Tích có hướng trong không gian ba chiều và các ứng dụng hình học

Tích có hướng là một phép toán quan trọng trong hình học không gian, giúp giải quyết nhiều bài toán về diện tích, thể tích và góc giữa các vector. Phép toán này mở rộng từ tích có hướng trong mặt phẳng lên không gian ba chiều Oxyz.

Công thức tính tích có hướng trong không gian Oxyz

Tích có hướng trong tọa độ không gian được xác định thông qua định thức cấp 3 của ma trận tọa độ. Với hai vector a(x1,y1,z1) và b(x2,y2,z2), tích có hướng của chúng được tính theo công thức:

[a,b] = |i j k |

|x1 y1 z1|
|x2 y2 z2|

Kết quả là một vector vuông góc với cả hai vector ban đầu và có độ dài bằng diện tích hình bình hành tạo bởi hai vector đó. Điều đặc biệt là vector kết quả tuân theo quy tắc bàn tay phải.

Tích có hướng của ba vector và diện tích hình bình hành

Tích có hướng của ba vector là một số vô hướng, biểu thị thể tích của hình hộp xiên tạo bởi ba vector đó. Giống như cách tính công thức tính cạnh tam giác thường, phép tính này giúp ta xác định được các yếu tố hình học một cách chính xác.

Với ba vector a, b, c, ta có công thức:
V = [a,b,c] = |x1 y1 z1|
|x2 y2 z2|
|x3 y3 z3|

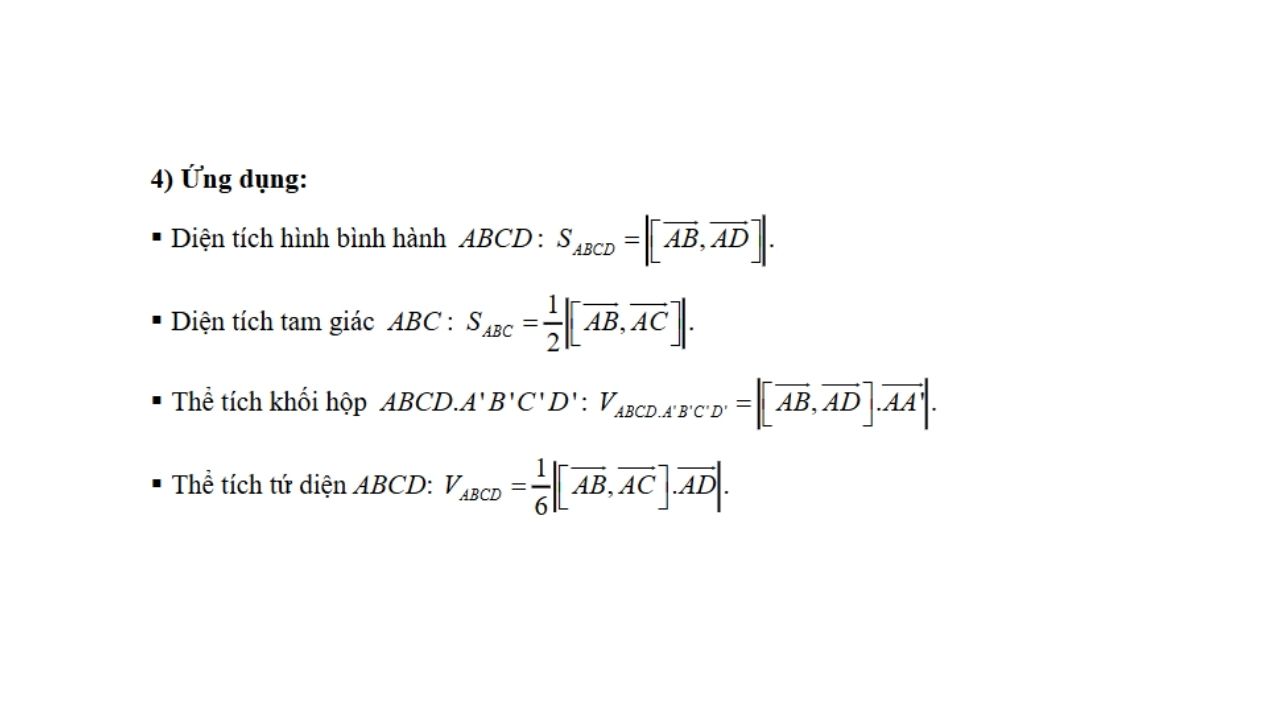
Bài tập mẫu về tích có hướng trong không gian

Cho hai vector a(1,2,3) và b(2,1,-1). Tính tích có hướng [a,b].

Giải:
[a,b] = |i j k |
|1 2 3 |
|2 1 -1 |
= (2.(-1) – 3.1)i – (1.(-1) – 3.2)j + (1.1 – 2.2)k
= -5i – (-1 – 6)j + (1 – 4)k
= -5i – (-7)j – 3k
= -5i + 7j – 3k

Kết quả cho thấy vector tích có hướng vuông góc với cả hai vector ban đầu và có độ dài bằng diện tích hình bình hành tạo bởi hai vector a và b.

So sánh tích có hướng và tích vô hướng trong toán học và vật lý

Xem thêm : Tìm hiểu về công thức tính góc giữa 2 vectơ

Tích có hướng và tích vô hướng là hai phép toán quan trọng trong toán học và vật lý, mỗi phép toán có những đặc điểm và ứng dụng riêng. Để hiểu rõ hơn về hai phép toán này, chúng ta sẽ phân tích từng khía cạnh.

Điểm khác biệt cơ bản giữa hai phép tính

Tích có hướng và tích vô hướng có những điểm khác biệt cơ bản về bản chất và kết quả. Tích vô hướng của hai vector cho kết quả là một số vô hướng, được tính bằng tích độ lớn của hai vector nhân với cos của góc giữa chúng. Ví dụ: Khi tính tích vô hướng của hai vector a(3,4) và b(1,2), ta được một số thực duy nhất.

Ngược lại, tích có hướng (hay còn gọi là tích vector) cho kết quả là một vector mới, có độ lớn bằng tích độ lớn hai vector nhân với sin của góc giữa chúng, và có phương vuông góc với mặt phẳng chứa hai vector ban đầu. Vector kết quả tuân theo quy tắc bàn tay phải để xác định chiều.

Ứng dụng của tích có hướng trong vật lý

Tích có hướng trong vật lý được ứng dụng rộng rãi trong nhiều lĩnh vực. Trong điện từ học, tích có hướng giúp tính lực từ tác dụng lên một dòng điện đặt trong từ trường. Công thức F = IL × B cho thấy lực từ F là tích có hướng của vector chiều dài dây dẫn L và vector cảm ứng từ B.

Trong cơ học, tích có hướng được sử dụng để tính moment lực, moment động lượng và các đại lượng vật lý khác có tính chất vector. Ví dụ khi một lực F tác dụng lên một điểm cách trục quay một khoảng r, moment của lực được tính bằng tích có hướng M = r × F.

Bài tập vận dụng phân biệt hai phép tính

Cho hai vector a = 2i + 3j và b = -i + 2j. Tính:

• Tích vô hướng a.b

• Tích có hướng a×b

Lời giải:
Tích vô hướng: a.b = 2×(-1) + 3×2 = -2 + 6 = 4
Tích có hướng: a×b = (2×2 – 3×(-1))k = (4 + 3)k = 7k

Qua bài tập trên, ta thấy rõ sự khác biệt: tích vô hướng cho kết quả là số 4, còn tích có hướng cho kết quả là vector 7k theo phương vuông góc với mặt phẳng chứa hai vector ban đầu.

FAQ: Câu hỏi thường gặp về tích có hướng

Tích có hướng là một phép toán quan trọng trong hình học vector. Để giúp các bạn hiểu rõ hơn về khái niệm này, tôi sẽ giải đáp một số câu hỏi thường gặp.

Cách tính tích có hướng của vector đơn vị?

Tích có hướng của vector đơn vị được tính bằng cách nhân độ dài hai vector và cos của góc giữa chúng. Do vector đơn vị có độ dài bằng 1 nên kết quả chỉ phụ thuộc vào cos của góc giữa chúng. Ví dụ, nếu hai vector đơn vị vuông góc với nhau, tích có hướng sẽ bằng 0 vì cos 90° = 0.

Mối quan hệ giữa tích có hướng và góc giữa hai vector?

Tích có hướng và góc giữa hai vector có mối quan hệ mật thiết thông qua hàm cos. Khi góc giữa hai vector là 0°, tích có hướng đạt giá trị lớn nhất. Ngược lại, khi góc là 180°, tích có hướng đạt giá trị nhỏ nhất. Điều này giúp xác định vị trí tương đối giữa các vector trong không gian.

Ứng dụng của tích có hướng trong hình học?

Tích có hướng trong hình học được ứng dụng rộng rãi để tính diện tích hình bình hành, xác định vector pháp tuyến của mặt phẳng và kiểm tra tính vuông góc của các vector. Một ví dụ điển hình là việc sử dụng tích có hướng để tính công cơ học khi lực tác động theo một góc so với phương chuyển động.

Kiến thức về **công thức tích có hướng** là nền tảng quan trọng trong hình học vector và ứng dụng thực tiễn. Các công thức tính toán đã được trình bày chi tiết từ cơ bản đến nâng cao, kèm theo các ví dụ minh họa cụ thể giúp người học dễ dàng tiếp cận. Việc nắm vững các tính chất và phương pháp tính tích có hướng mở ra nhiều ứng dụng thiết thực trong toán học và vật lý, đặc biệt trong không gian ba chiều và các bài toán hình học vector.

Nguồn: https://congthuctoan.com
Danh mục: Góc và vectơ