Công thức Pytago và bài tập minh họa

Công thức Pytago là một trong những định lý quan trọng trong chương trình Toán học hình học. Tìm hiểu về công thức này giúp bạn biết cách áp dụng vào các bài toán từ đơn giản đến nâng cao.

Lý thuyết công thức Pitago

Công thức định lý Pytago được áp dụng trong Toán hình học. Đây là công thức cơ bản về tam giác vuông mà học sinh cần nắm vững. Định lý Pytago áp dụng trong việc tính độ dài các cạnh của một tam giác vuông.

Bạn đang xem: Công thức Pytago và bài tập minh họa

Định lý này có thể dùng để dựng đoạn thẳng vô cước. Chính là biểu hiện độ dài các cạnh của tam giác vuông mà cả ba độ dài cạnh này là những số nguyên dương.

Định lý Pytago thuận

Định lý Pytago thuận được phát biểu rằng: Trong một tam giác vuông, bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương hai cạnh góc vuông.

Ví dụ: Cho tam giác vuông ABC vuông tại A. Độ dài các cạnh AB = a, AC = b, BC = c. Áp dụng định lý Pytago thuận, công thức được thể hiện như sau:

BC² = AB² + AC²

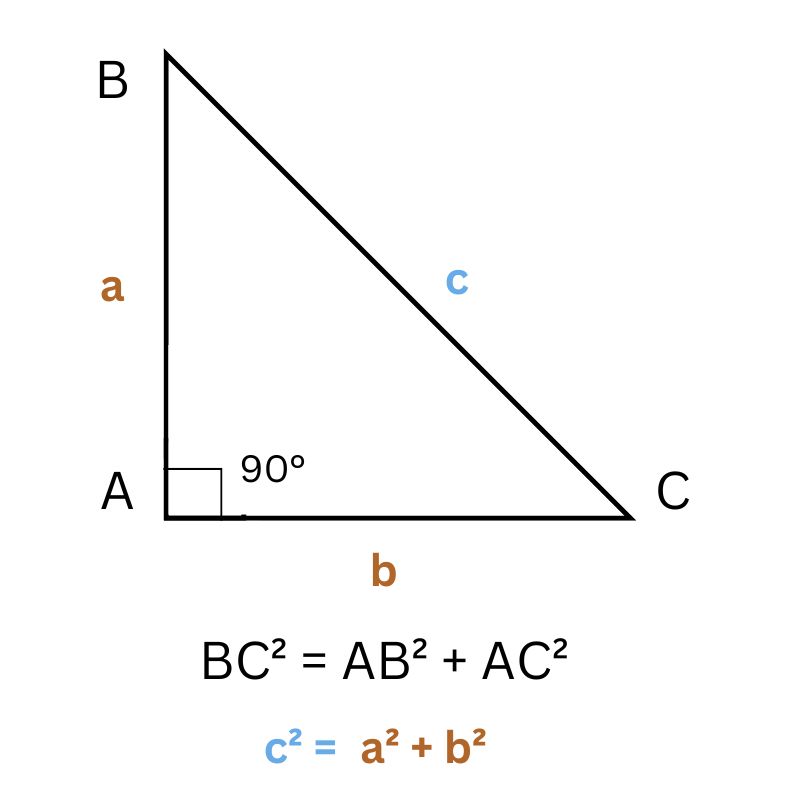
Định lý Pytago đảo

Theo định lý Pytago đảo nghịch: Nếu một tam giác có bình phương một cạnh bằng tổng bình phương hai cạnh còn lại thì tam giác đó là tam giác vuông. Định lý này được ứng dụng cho các bài toán chứng minh tam giác vuông.

Bài toán này sẽ được thực hiện theo các bước sau:

• Bước 1: Tính bình phương độ dài các cạnh của tam giác.
• Bước 2: So sánh bình phương cạnh lớn nhất với tổng các bình phương của hai cạnh còn lại.
• Bước 3: Nếu hai kết quả bằng nhau thì ta suy ra tam giác đó là tam giác vuông và cạnh lớn nhất là cạnh huyền.

Ví dụ: Cho tam giác ABC, độ dài các cạnh lần lượt là  AB = a, AC = b, BC = c. Áp dụng định lý Pitago đảo,  AB² + AC² = BC², thì suy ra ABC là tam giác vuông.

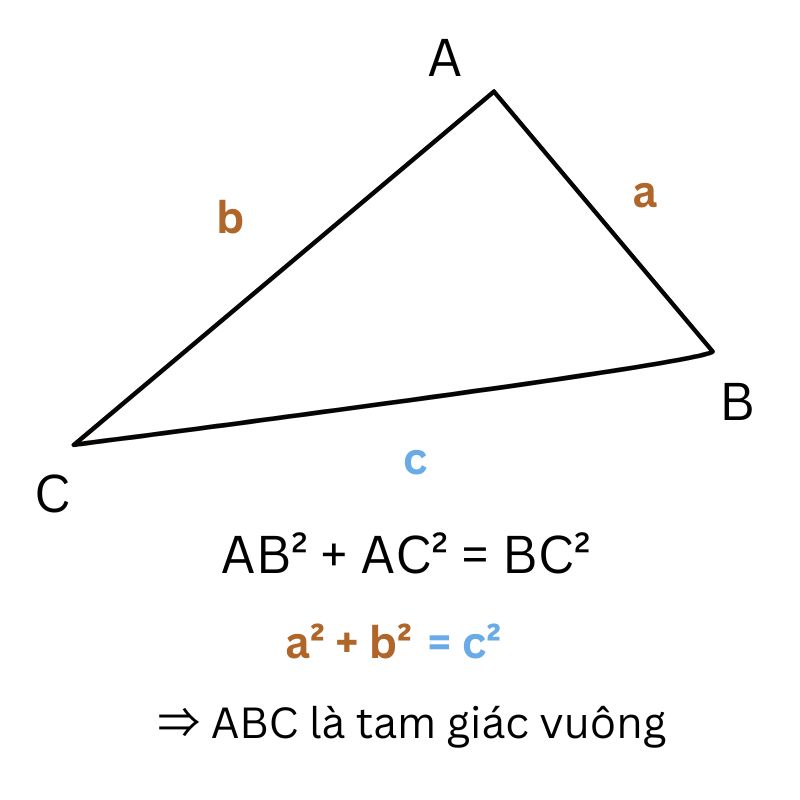
Hệ quả của định lý Pytago đảo là có thể xác định một tam giác có là tam giác vuông, hay tam giác nhọn hoặc tam giác tù. Cụ thể như sau:

Ta gọi c là cạnh dài nhất của một tam giác và a + b > c. Từ đó cho ta thấy các phát biểu sau đây là đúng:

• Nếu a² + b² = c², tam giác là tam giác vuông.
• Nếu a² + b² > c², tam giác là tam giác nhọn.
• Nếu a² + b² < c², tam giác là tam giác tù.

Cách chứng minh định lý Pytago công thức

Dựa vào hình dưới đây để chứng minh định lý này một cách đơn giản nhất.

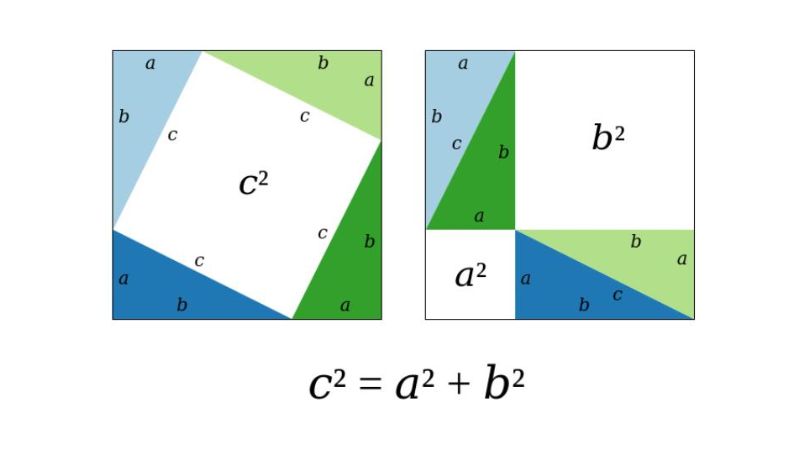
Dựa vào hình trên cho ta thấy 2 hình vuông lớn có diện tích bằng nhau là: (a + b)². Trong mỗi hình vuông lại có 4 hình tam giác vuông bằng nhau. Tổng diện tích bằng nhau là 1/2(a.b). Điều này chứng minh, diện tích khoảng trắng của 2 hình đều bằng nhau.

Như vậy, diện tích của hình vuông c bằng tổng diện tích của 2 hình vuông a và b nên ta có công thức như sau: c² = a² + b². Bạn có thể áp dụng cách giải này cho các bài tập trong sách giáo khoa.

Một số bài tập áp dụng công thức Pytago

Học sinh thực hành giải các đề toán về Pytago và tam giác vuông từ cơ bản đến nâng cao. Điều này sẽ giúp bạn rèn luyện và ôn tập kiến thức một cách hiệu quả. Nhờ ôn tập đúng cách bạn có thể đạt điểm cao trong môn học này.

Bài tập

Bài 1: Cho tam giác ABC có độ dài các cạnh AC = 5cm, BC = 3cm, AB = 4cm. Tam giác ABC là tam giác gì?

Bài 2: Xét ABC là tam giác vuông tại A, biết:

1. Chiều dài cạnh AB = 4cm, chiều dài cạnh BC = 6cm. Tính chiều dài cạnh AC.
2. Chiều dài cạnh AC = 2cm, chiều dài cạnh BC = 7cm. Tính chiều dài cạnh AB.
3. Chiều dài cạnh AB = 3cm, chiều dài cạnh AC = 5cm. Tính chiều dài cạnh BC.

Bài 3:  Hãy tính chiều dài cạnh huyền của các tam giác sau, biết rằng:

1. Tam giác AMN vuông tại A có cạnh AN = 4cm, cạnh AM = 5cm.
2. Tam giác BDO vuông tại B có cạnh BD = 7cm, cạnh BO = 6cm.
3. Tam giác ECD vuông tại E có cạnh EC = 8cm, cạnh ED = 2cm.
4. Tam giác IKC vuông tại I có cạnh IK = 8cm, cạnh IC = 4,5cm.

Xem thêm : Tìm hiểu công thức tính khoảng cách từ điểm đến đường thẳng và bài tập áp dụng chi tiết

Bài 4: Cho tam giác ABC có độ dài AB = 6cm, AC = 8cm, BC = 10cm. Chứng minh góc BAC = 90°.

Bài giải gợi ý

Bài 1: Áp dụng công thức BC² + AB² = AC²

BC² = 3² = 9

AB² = 4² = 16

AC² = 5² = 25

⇔  3² + 4² = 5²

⇔ 9 + 16 = 25 = AC²

⇒ ABC là tam giác vuông tại B (định lý Pytago đảo).

Bài 2:

a. Ta có : BC²  = AC² + AB²

⇔ AC² = BC² – AB²

⇔ AC² = 62 – 42

⇒ AC = căn bậc hai của 20 (cm).

b. Ta có: BC²  = AC² + AB²

⇔ AB² = BC² – AC²

⇔ AC² = 7² – 2²

⇒ AC = căn bậc hai của 45 (cm).

c. Ta có: BC²  = AC² + AB²

Xem thêm : Lý thuyết công thức tính bán kính hình tròn và bài tập mẫu chi tiết

⇔ BC² = 3² + 5²

⇒ BC = căn bậc hai của 34 (cm).

Bài 3:

Tam giác AMN vuông tại A, MN là cạnh góc vuông. Từ đó, bạn áp dụng định lý Pytago trong tam giác vuông:

MN²= AN² + AM²

⇔ MN² = 4² + 5²

⇒ MN² = 41

⇒ MN = căn bậc hai của 41(cm).

(Bài tập phần b, c, d có cách giải tương tự).

Bài 4: Ta có:

AB² = 62  = 36

AC² = 82 = 64

BC² = 102 = 100

Áp dụng công thức định lý Pytago:

AB² + AC² = BC²

⇔ 36 + 64 = 100 = BC²

⇒ ABC là tam giác vuông tại A (theo định lý Pytago đảo).

⇒ Góc BAC = 90° (điều phải chứng minh).

Kết luận

Tìm hiểu công thức Pytago rất có lợi trong việc học Toán của học sinh. Bạn có thể tự ôn tập tại nhà bằng cách giải bài tập tham khảo. Điều này rất có ích trong việc rèn luyện và nâng cao kiến thức.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng