Bảng tổng hợp công thức lượng giác (đầy đủ)

Trong bảng công thức lượng giác từ cơ bản, đến nâng cao, kết hợp với công thức nghiệm của phương trình. Nắm rõ công thức được ứng dụng phổ biến và hiểu rõ cách tính giúp học sinh học toán dễ dàng hơn.

Tổng hợp các công thức liên quan đến cung đặc biệt

Chi tiết bảng công thức lượng giác theo các cung liên quan đặc biệt. Nhóm Nhóm công thức này bao gồm: Cung đối nhau, bù nhau, phụ nhau và hơn kém và 2.

Bạn đang xem: Bảng tổng hợp công thức lượng giác (đầy đủ)

1. Công thức cơ bản của hai cung đối nhau

Hai cung đối nhau gồm: sin và -sin, cos và -cos, tan với -tan và cot với -cot.

2. Công thức hai cung bù nhau lượng giác

Hai cung bù nhau cũng có công thức lượng giác:

3. Công thức tính cho 2 cung phụ nhau

4. Công thức tính cung hơn kém pi:

5. Cung hơn kém pi/2

Công thức cơ bản và công thức cộng

Công thức cộng cơ bản và công thức cộng cũng khá đơn giản, bạn nên lưu ý để ứng dụng khi giải đoán.

1. Công thức sin cos cơ bản

2. Công thức cộng cos sin phổ biến

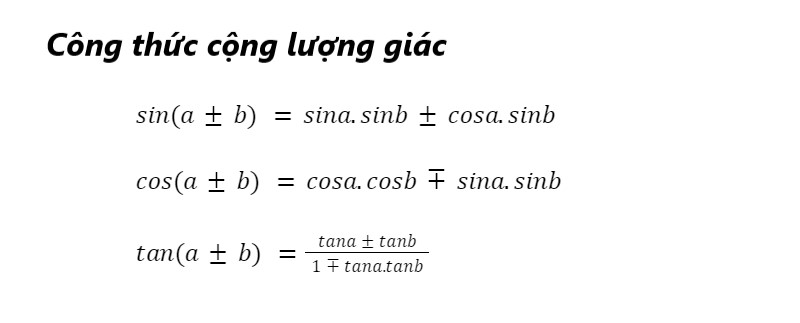
3. Công thức nhân đôi thường gặp khi tính toán

Xem thêm : Công thức hệ thức lượng Thức Hệ Thức Lượng Tam Giác Lượng

Bạn tham khảo công thức nhân đôi và nhân ba khi tính hàm theo bảng:

4. Công thức cos sin hạ bậc

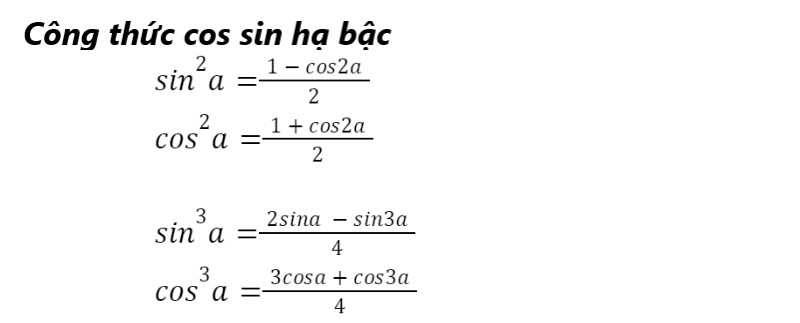
5. Công thức cosin biến đổi tổng thành tích

6. Công thức cos sin biến đổi tích thành tổng

Công thức thể hiện nghiệm phương trình cơ bản

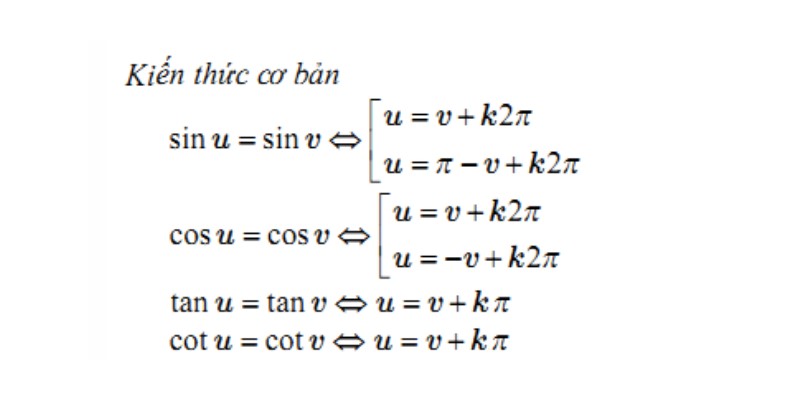
Trường hợp đặc biệt của công thức nghiệm:

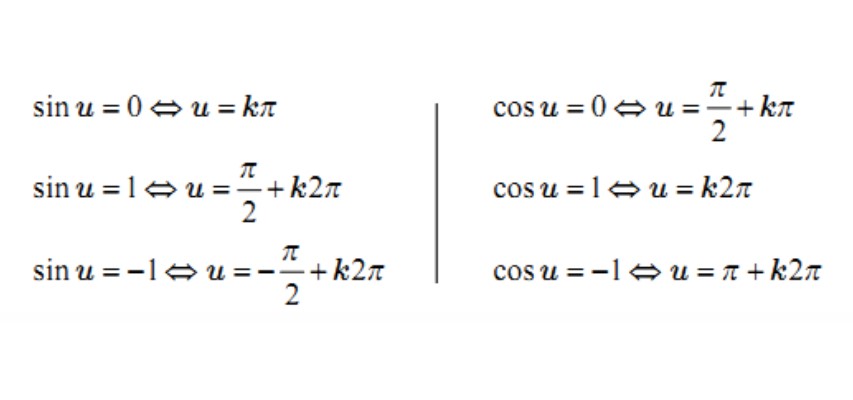
Các dạng bài tập liên quan đến công thức sin cos tan

Có nhiều dạng bài tập liên quan đến lượng giác kèm cách giải giúp bạn tìm ra đáp án dễ dàng.

Dạng 1: Tìm giá trị lượng giác góc đặc biệt

Với dạng bài này, bạn dùng định nghĩa chỉ giá trị lượng giác của góc. Căn cứ vào tính chất, bảng giá trị lượng giác đặc biệt sẽ giúp học sinh giải ra đáp án.

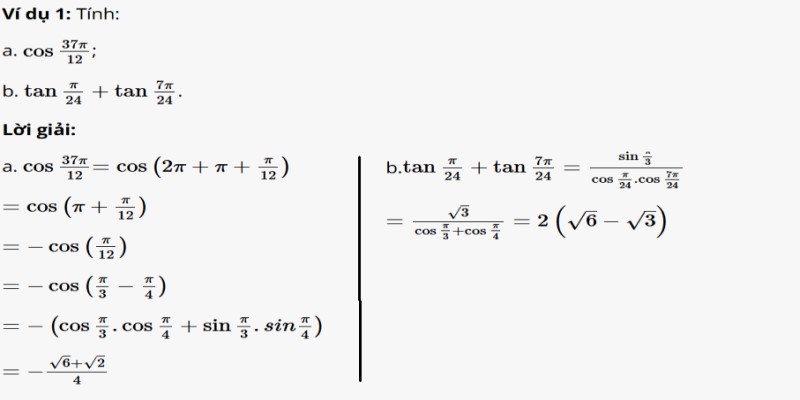
Dạng 2: Chứng minh đẳng thức lượng giác

Với dạng bài tập này, bạn có thể dùng các công thức gồm:

• Cộng
• Nhân đôi
• Hạ bậc
• Biến đổi tổng thành tích
• Biến đổi tích thành tổng.
• Góc liên quan đặc biệt.

Xem thêm : Hướng dẫn học công thức biến đổi tích thành tổng và bài tập

Có 3 cách để học sinh có thể chứng minh đẳng thức gồm:

• Dạng 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại.
• Dạng 2: Biến đổi đẳng thức về một đẳng thức đã biết luôn đúng.
• Dạng 3: Biến đổi đẳng thức đã biết luôn đúng thành đẳng thức cần chứng minh.

Giải bài tập liên quan đến lượng giác

Để bạn có thể nghiên cứu một số mẫu bài tập tiêu biểu thường dùng nhất liên quan đến lượng giác.

Bài 1: Chứng minh các công thức là đúng

Bạn quan sát hình minh họa để nắm nội dung đề bài đưa ra và cách giải chi tiết. Bài tập này rất phổ biến, yêu cầu người giải chứng minh được công thức trong đề bài.

Bài 2:  Cho tam giác ABC, chứng minh:

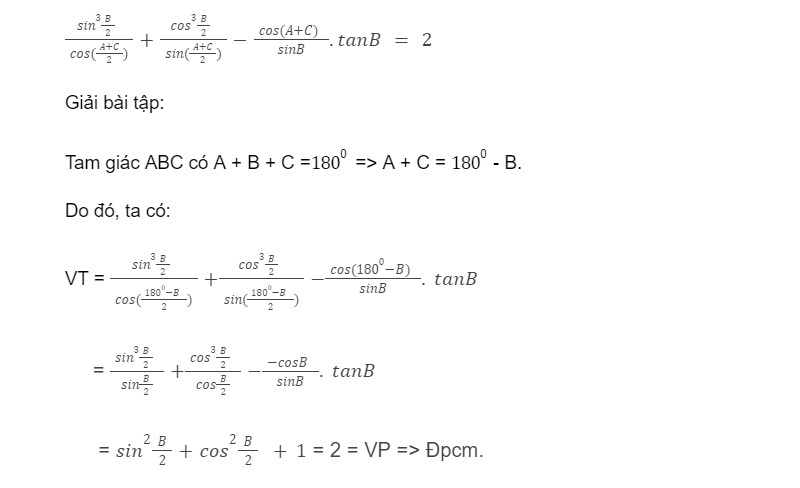
Kết luận

Công thức lượng giác xuất hiện trong nhiều lĩnh vực khác nhau. Căn cứ vào từng trường hợp, bạn cần xác định từng dạng bài tập và tìm ra cách giải chính xác.

Nguồn: https://congthuctoan.com
Danh mục: Lượng giác