Sử dụng công thức liên hợp để giải Toán lớp 9

Công thức nhân liên hợp là kiến thức bạn có thể áp dụng để giải các bài toán căn bậc 2 và căn bậc 3. Đồng thời, đây cũng là kiến thức trọng tâm học sinh cần nắm rõ trong quá trình học.

Cách sử dụng biểu thức liên hợp để giải toán

Một số biểu thức liên hợp thường gặp trong trường trình Toán học lớp 9. Bạn cần nắm vững những biểu thức này để có thể áp dụng vào bài tập.

Bạn đang xem: Sử dụng công thức liên hợp để giải Toán lớp 9

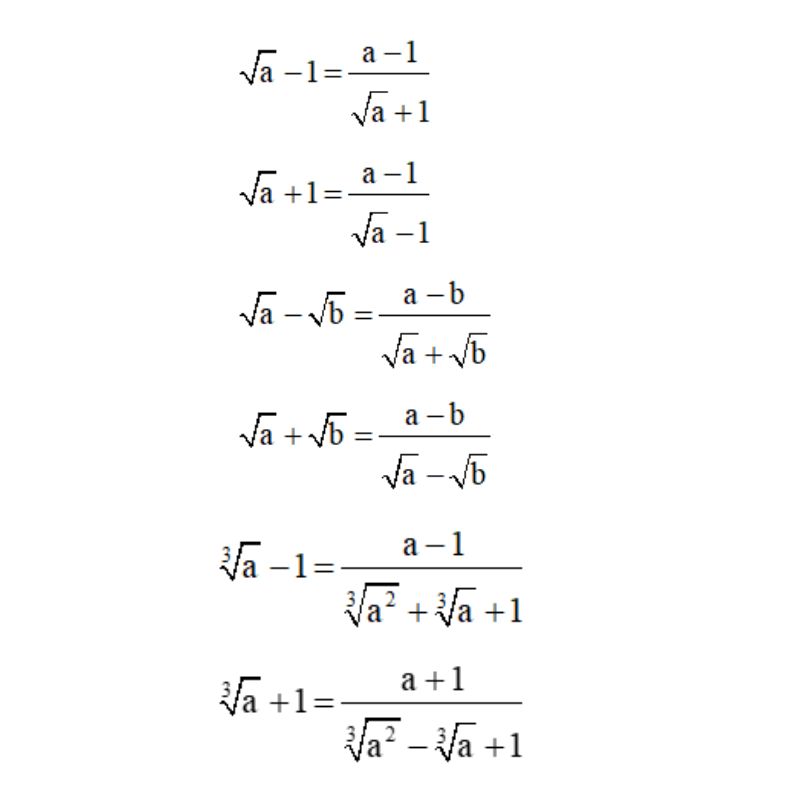
Một số dạng bài tập sử dụng biểu thức liên hợp

Có rất nhiều dạng bài tập có thể áp dụng biểu thức liên hợp căn bậc 2, căn bậc 3 để tính. Sau đây là gợi ý một số bài tập và hướng dẫn cách giải cho học sinh tham khảo. Điều này có thể giúp bạn tự ôn luyện và nâng cao kiến thức.

Dạng 1: Bài toán sử dụng biểu thức liên hợp để tính giá trị phương trình căn bậc 2, căn bậc 3

Phương pháp giải bài tập này là sử dụng các phép tính nhân liên hợp để biến đổi biểu thức thành biểu thức đơn giản hơn. Sau đó ta có thể thực hiện theo thứ tự phép tính thông thường.

Ví dụ: Tính giá trị biểu thức

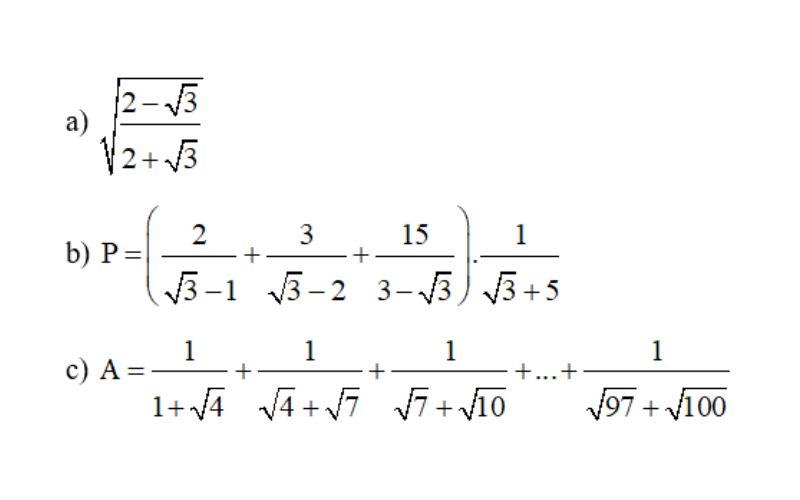
Bài giải:

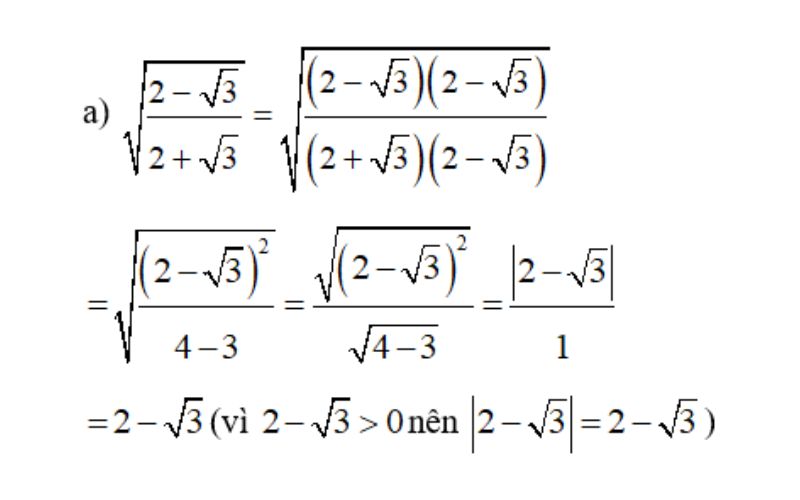
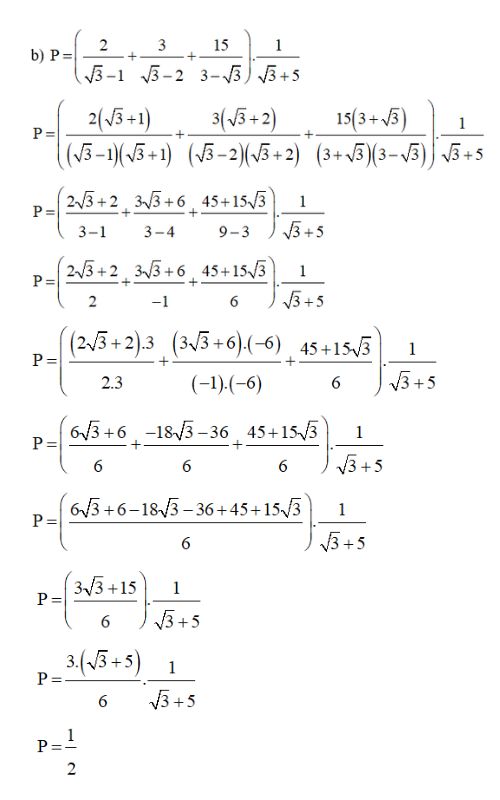
Dạng 2: Bài toán sử dụng biểu thức nhân liên hợp để rút gọn phương trình căn bậc 2, căn bậc 3

Ta áp dụng phương pháp giải sử dụng biểu thức liên hợp để biến đổi và rút gọn biểu thức căn bậc 2, căn bậc 3.

Ví dụ: Rút gọn biểu thức

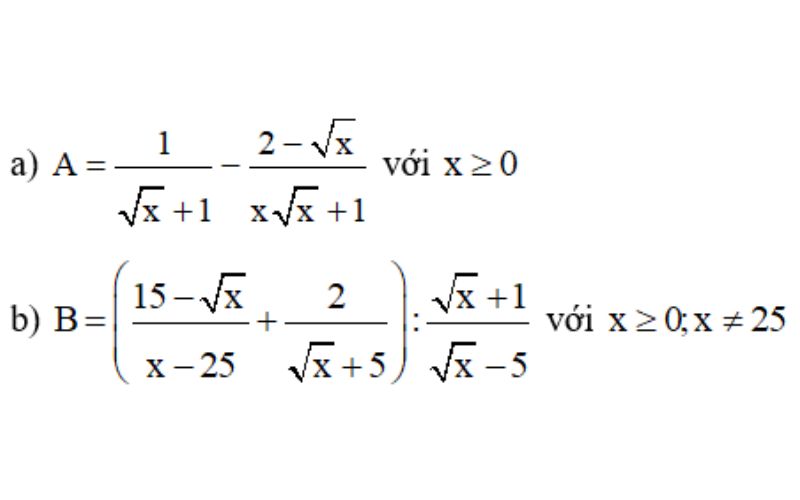
Bài giải:

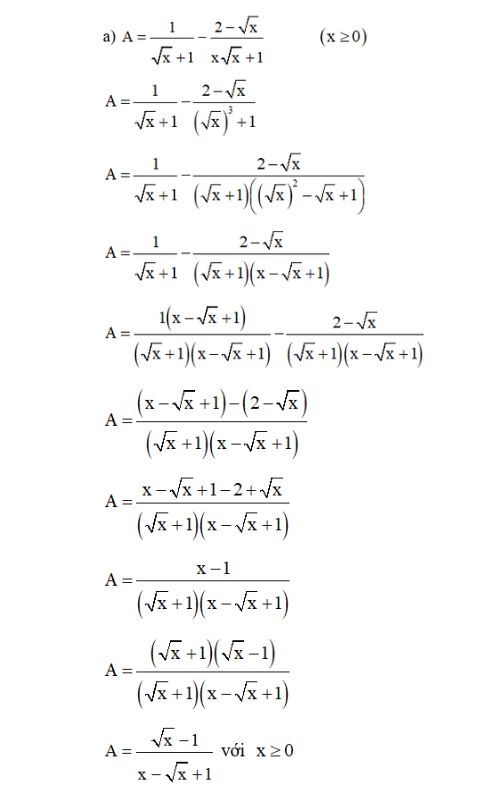
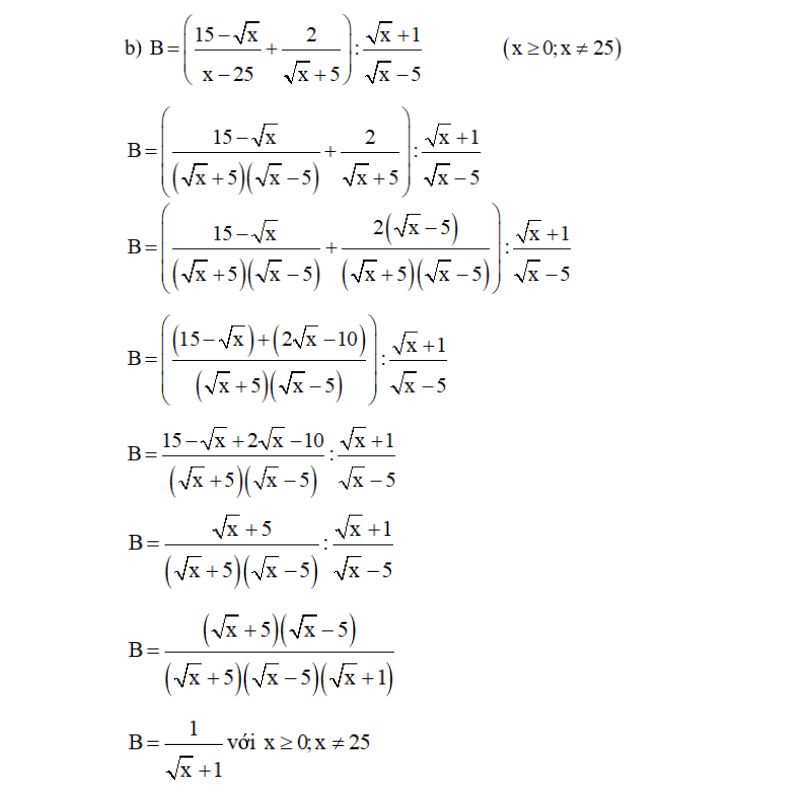
Dạng 3: Bài toán chứng minh x0 là nghiệm của phương trình

Ta có thể dùng các biểu thức liên hợp đưa nghiệm x₀ về số đơn giản. Sau đó thay x0 vào phương trình và chứng minh x₀ là nghiệm.

Xem thêm : Công thức Viet và ứng dụng trong Toán

Ví dụ: Chứng minh x₀ là nghiệm của phương trình x³ – 6x – 10=0. Biết rằng:

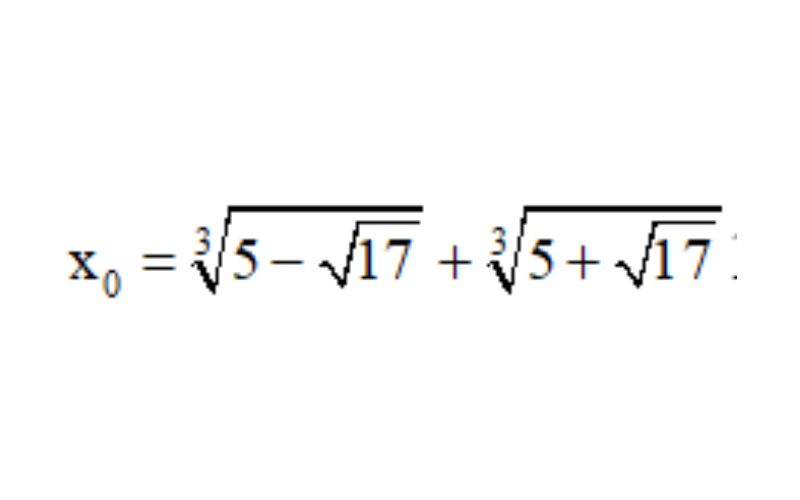
Bài giải:

Gợi ý bài tập thực hành

Bài 1: Thực hiện các phép tính

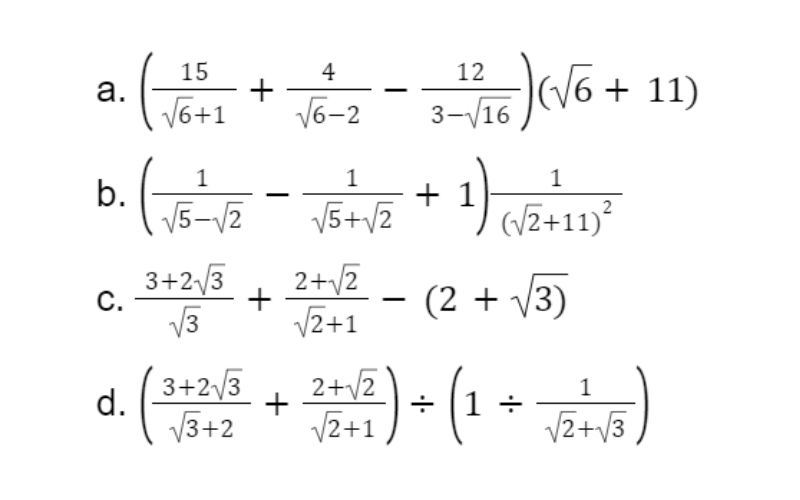
Bài 2: Rút gọn biểu thức

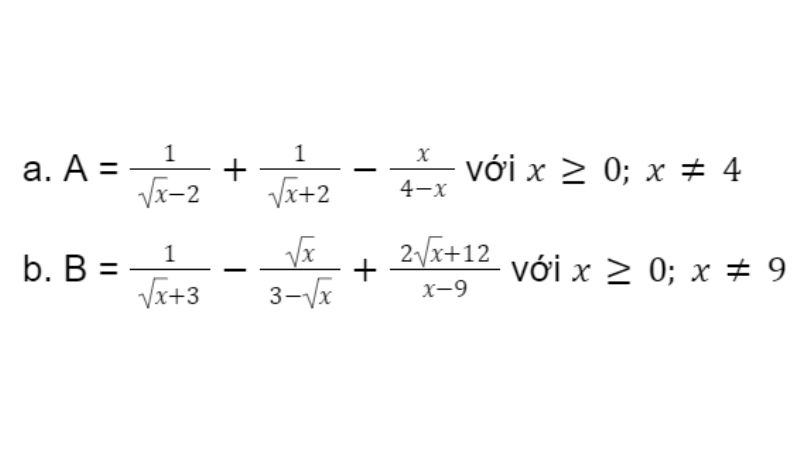
Kết luận

Áp dụng công thức liên hợp có thể giúp học sinh dễ dàng giải những bài toán căn bậc 2, căn bậc 3. Do đó, bạn cần hiểu và nắm vững được nội dung kiến thức này. Nhờ điều này có thể giúp bạn đạt điểm cao trong môn học.

Nguồn: https://congthuctoan.com
Danh mục: Đại số