Trang chủ » Công thức hệ thức lượng trong tam giác đầy đủ và chi tiết

Công thức hệ thức lượng trong tam giác đầy đủ và chi tiết

Công thức hệ thức lượng là phần nội dung đặc biệt quan trọng, đóng vai trò nền tảng trong chương trình đào tạo. Để học tốt các môn học tự nhiên như toán, lý,.. việc hiểu rõ bản chất và ghi nhớ chính xác là cần thiết.

Có thể bạn quan tâm

Table of Contents

Công thức hệ thức lượng trong tam giác vuông

Tam giác vuông là một loại tam giác đặc biệt. Học sinh cần nằm lòng những định lý cơ bản để dễ dàng vận dụng trong quá trình giải bài tập.

Bạn đang xem: Công thức hệ thức lượng trong tam giác đầy đủ và chi tiết

1/ Một số khái niệm cơ bản

Công thức lượng giác là tập hợp những biểu thức thể hiện mối liên hệ giữa các cạnh và góc trong một tam giác vuông.

Đây là kiến thức trọng tâm trong chương trình giảng dạy trung học. Việc nắm vững các nguyên lý là điều kiện cần để học sinh có thể hiểu và theo kịp các nội dung kế tiếp.

2/ Công thức lượng giác trong tam giác vuông giữa các cạnh và đường cao

Trong tam giác ABC, góc A = 90 độ, có đường cao AH. Mối liên hệ giữa các cạnh và đường cao được xác định dựa trên các định lý sau.

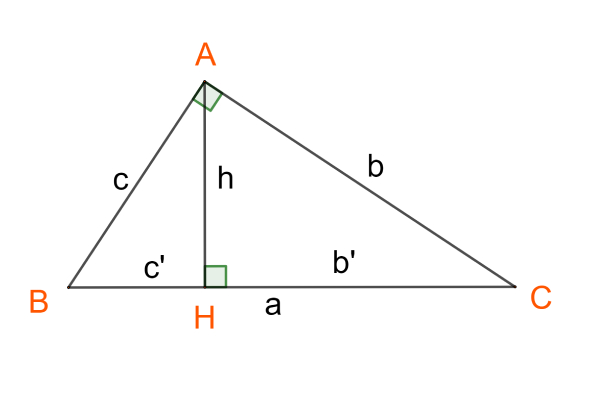
công thức hệ thức lượng — Công thức lượng giác giữa cạnh và đường cao trong tam giác vuông

Định lý 1

Bình phương cạnh góc vuông bằng tích của cạnh huyền và hình chiếu tương ứng của cạnh góc vuông đó trên cạnh huyền.

AB2 = BH * BC

AC2 = CH * BC

Định lý 2

Bình phương đường cao bằng tích hình chiếu tương ứng của hai cạnh góc vuông đó trên cạnh huyền.

AH2 = BH * CH

Định lý 3

Tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao ứng với cạnh huyền.

AB * AC = AH * BC

Định lý 4

Nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng nghịch đảo của bình phương hai cạnh góc vuông.

1/AH2 = 1/AB2 * 1/AC2

3/ Công thức hệ thức lượng trong tam giác vuông giữa góc và cạnh

công thức tam giác vuông — Tam giác ABC có một góc vuông tại A

Trong tam giác ABC vuông tại A, các cạnh và góc có mối quan hệ mật thiết với nhau:

Định lý 1

Độ dài cạnh góc vuông bằng tích của cạnh huyền và Sin góc đối diện, bằng tích của cạnh huyền và Cos góc nhọn liền kề

AC= BC * Sin B = BC * Cos C

AB = BC * Sin C = BC * Cos B

Định lý 2

Xem thêm : Lý thuyết công thức tính bán kính hình tròn và bài tập mẫu chi tiết

Độ dài cạnh góc vuông bằng tích của cạnh góc vuông còn lại và Tan góc đối diện, bằng tích của cạnh góc vuông còn lại và Cot góc nhọn liền kề.

AC = AB * TanB = AB * Cot C

AB = AC * TanC = AC * Cot B

Tỉ số lượng giác góc nhọn trong tam giác vuông

Tham khảo tỉ số lượng giác góc nhọn quen thuộc, thường xuyên được sử dụng hiện nay.

1/ Một số khái niệm

Tỉ số lượng giác góc nhọn là các tỉ số thể hiện mối quan hệ giữa góc nhọn và các cạnh trong một tam giác vuông.

Gọi a là số đo góc của một góc nhọn trong tam giác vuông. Tỉ số lượng giác được xác định như sau:

Sina = Cạnh đối/Cạnh huyền
Cosa = Cạnh kề/Cạnh huyền
Tana = Cạnh đối/Cạnh kề
Cota = Cạnh kề/Cạnh đối

2/ Một số công thức lượng giác góc nhọn cơ bản

Tana= Sina/Cosa
Tana*Cosa = 1
Tan2a + 1 = 1/Cos2a
Cota = Cosa/Sina
Sin2a + Cos2a = 1
Cot2a + 1 = 1/Sin2a

3/ So sánh các tỉ số lượng giác

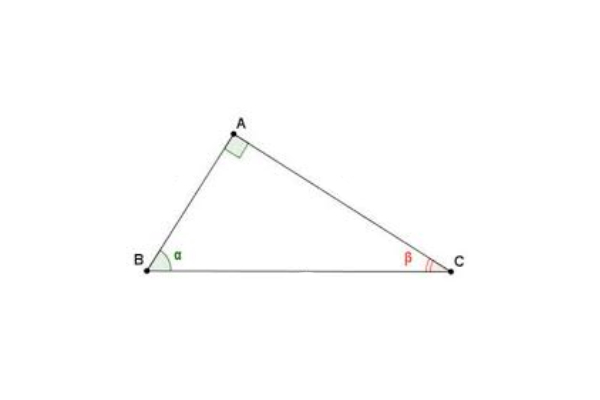
công thức lượng giác trong tam giác vuông — So sánh tỉ số lượng giác chuẩn xác trong tam giác vuông

Giả sử a và b là số đo hai góc nhọn trong một tam giác vuông (a < b). Ta có:

Sina < Sinb
Tana < Tanb
Cosa > Cosb
Cota > Cotb
Sina < Tana
Cosa < Cota

Công thức các cung liên kết trên đường tròn lượng giác

công thức tam giác — Tổng hợp công thức các cung liên kết trên đường tròn lượng giác

Trường hợp 1: Hai góc đối nhau

Cos(-x) = Cosx

Sin(-x) = – Sinx

Tan(-x) = – Tanx

Cot(-x) = – Cotx

Trường hợp 2: Hai góc bù nhau

Sin(π-x) = Sinx

Cos(π-x) = – Cosx

Tan(π-x) = – Tanx

Cot(π-x) = – Cotx

Trường hợp 3: Hai góc phụ nhau

Sin(π/2-x) = Cosx

Cos(π/2-x) = Sinx

Tan(π/2-x) = Cotx

Xem thêm : Công thức Pytago và bài tập minh họa

Cot(π/2-x) = Tanx

Trường hợp 4: Hai góc hơn kém nhau π

Sin(π+x) = – Sinx

Cos(π+x) = – Cosx

Tan(π+x) = Tanx

Cot(π+x) = Cotx

Trường hợp 5: Hai góc hơn kém nhau π/2

Sin(π/2+x) = Cosx

Cos(π/2+x) = – Sinx

Tan(π/2+x) = – Cotx

Cot(π/2+x) = – Tanx

Một số dạng toán thường gặp

Dưới đây là các dạng bài tập sử dụng công thức hệ thức lượng trong tam giác vuông điển hình.

1/ Xác định độ dài các cạnh, số đo các góc trong tam giác vuông

Có hai dạng cơ bản:

Dạng 1: Tính độ dài cạnh và số đo các góc còn lại khi biết độ dài một cạnh và số đo một góc nhọn.

Dạng 2: Tính độ dài cạnh và số đo các góc còn lại dựa vào độ dài hai cạnh cho trước.

Học sinh vận dụng các công thức tính sin, cos và mối liên hệ giữa các cạnh và góc trong tam giác để tìm đáp án chính xác.

2/ Chứng minh tam giác vuông

Bài toán yêu cầu chứng minh tam giác là tam giác vuông dựa trên một vài dữ liệu cho trước như số đo góc hoặc chiều dài cạnh.

Học sinh dựa vào các công thức hệ thức lượng để chứng minh một trong các nội dung sau:

Một trong các góc của tam giác bằng 90 độ
Tổng hai góc nhọn trong tam giác bằng 90 độ
Dựa trên định lý Pitago: Tam giác có bình phương độ dài một cạnh bằng tổng bình phương độ dài hai cạnh còn lại

3/ Chứng minh các hệ thức và tính giá trị biểu thức

Đề bài đưa ra một biểu thức nhất định và một vài giả thiết, thường dưới dạng tổng quát. Học sinh vận dụng các công thức lượng giác để biến đổi các vế của đẳng thức và đưa ra đáp án chính xác.