Công thức hệ thức lượng Thức Hệ Thức Lượng Tam Giác Lượng
Nghiên cứu công thức hệ thức lượng trong tam giác vuông được ứng dụng theo nguyên lý cơ bản đến phức tạp. Phép tính được thực hiện và ứng dụng nhiều trong toán hình học, cũng như nhiều lĩnh vực trong thực tiễn.
Tổng hợp công thức lượng giác trong tam giác vuông
Với công thức hệ thức lượng trong tam giác vuông gồm hệ thức về cạnh và góc. Học sinh có thể giải các bài toán theo những công thức này một cách dễ dàng.


Ví dụ minh họa đối với công thức về hệ thức lượng giác giúp bạn hình dung dễ hơn khi ứng dụng. Cho tam giác vuông ABC với góc A vuông, độ dài các cạnh là AB =3cm, AC=4cm.
Nếu áp dụng theo định lý Pitago có:

Hệ thức lượng trong tam giác vuông là gì?
Hệ thức lượng trong tam giác vuông là danh sách các công thức trong toán học dùng để tính cạnh và góc tam giác này theo các dữ liệu đã cho sẵn. Đây là kiến thức quan trọng đối với hình học phẳng, nhất là lĩnh vực nghiên cứu lượng giác.
- Hệ thức Pythagoras c^2 = a^2 + b^2, với c là cạnh huyền, a và b là cạnh góc vuông.
- Tỉ số lượng giác (sin, cos, tan, cot) được tính từ các cạnh của tam giác vuông, cho ra đáp án góc nhọn tam giác.
- Công thức khác: a = c.sin(B) = c.cos(C) giúp bạn tính độ dài cạnh thông qua cạnh huyền và góc tương ứng.
- Công thức a^2 =c.c’ cho thấy, đường cao tạo mối quan hệ giữa cạnh góc vuông và hình chiếu của cạnh này trên cạnh huyền.
- Công thức b = c.tan(B) = c.cot(C) cho biết liên hệ giữa các cạnh góc vuông qua góc nhọn đối diện.
Ứng dụng công thức tam giác vuông
Công thức hệ thức lượng trong tam giác vuông được dùng nhiều trong toán học. Đây cũng là công cụ ứng dụng phổ biến để đo lường, xây dựng kiến trúc và nhiều ngành kỹ thuật.

1. Dùng công thức hệ thức lượng trong đo lường
Hệ thức lượng giúp đo lường khoảng cách chính xác dù bạn không thể tiếp cận trực tiếp trong thực tế. Giả sử, với hệ thức lượng, bạn có thể tính toán khoảng cách giữa hai điểm qua sông bằng cách đặt điểm phụ trên bờ và ứng dụng công thức Pythagoras.
2. Áp dụng công thức hệ thức lượng giác trong xây dựng kiến trúc
Dùng công thức này cũng có thể ứng dụng trong thiết kế cấu trúc cầu thang. Áp dụng tính toán, bạn có thể xác định được các góc nghiêng an toàn, chiều dài của cầu thang thích hợp để mang đến sự tiện lợi khi sử dụng.
3. Dùng hệ thức lượng trong ngành hàng không
Bên cạnh ứng dụng trong tính khoảng cách, xây dựng kiến trúc, bạn cũng có thể áp dụng công thức này trong lĩnh vực hàng không. Hệ thức lượng được áp dụng tính góc hạ cánh, giúp máy bay giảm độ cao khi hạn cánh trong khoảng an toàn.
Ví dụ minh họa dùng công thức hệ thức lượng tam giác vuông
Dùng công thức tính hệ thức lượng cũng giúp học sinh có thể giải bài tập một cách dễ dàng. Những minh họa cụ thể để bạn có thể hiểu các mối liên hệ của những yếu tố trong tam giác vuông.
1. Bài tập 1: Cho tam giác ABC vuông tại A có cạnh huyền BC = 5cm, AB = 3cm. Tính sin, cos góc B?
Áp dụng định lý Pythagoras có:
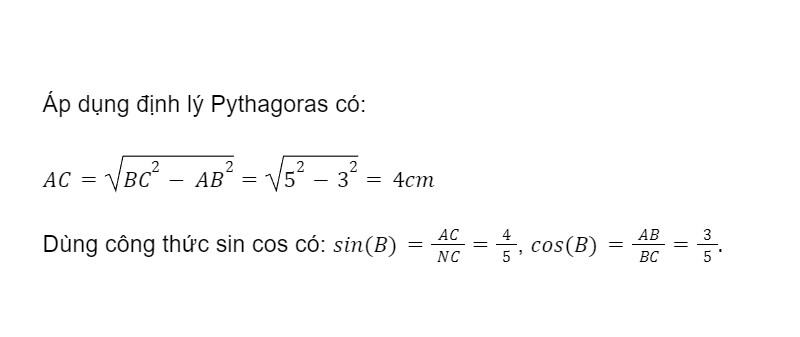
2. Bài tập 2: Cho tam giác ABC (Góc A vuông) có đường cao AH, biết AB = 6cm, BC = 10cm. Tính AH?
Với đề bài này, bạn có thể theo dõi nội dung trong hình minh hoạ nhằm hiểu rõ cách giải:
Dùng hệ thức về đường cao trong tam giác vuông cho thấy AH2=BH.CH.

3. Bài tập 3: Cho tam giác ABC vuông tại A, với AB = 5, AC = 8. Tính BC?
Áp dụng định lý Pythagoras, ta có: BC được tính bằng căn bậc hai của (AB^2 + AC^2), từ đó tính được đáp án BC = 9.43.
Kết luận
Tính toán công thức hệ thức lượng được sử dụng thường xuyên trong hình không gian. Học sinh cần hiểu rõ và nắm đúng các phép tính chuẩn, qua đó có thể ứng dụng để tìm được các yếu tố đang quan tâm.
Nguồn: https://congthuctoan.com
Danh mục: Lượng giác
Bài viết liên quan

Hướng dẫn học công thức biến đổi tích thành tổng và bài tập
Công thức biến đổi tích thành tổng nằm trong các công thức lượng giác nhất định phải nhớ. Nắm vững kiến thức này giúp bạn đơn giản hoá các bài tập toán học và đạt điểm cao.Có thể bạn quan tâm Công thức hạ bậc là gì? Tổng hợp công thức hạ bậc lượng giác […]

Công thức hạ bậc là gì? Tổng hợp công thức hạ bậc lượng giác
Công thức hạ bậc là một trong những khái niệm quan trọng bậc nhất của bộ môn Lượng giác. Nắm vững kiến thức này giúp bạn nhanh chóng giải được các bài về tích phân cũng như các phương trình phức tạp.Có thể bạn quan tâm Bảng tổng hợp công thức lượng giác (đầy đủ) […]
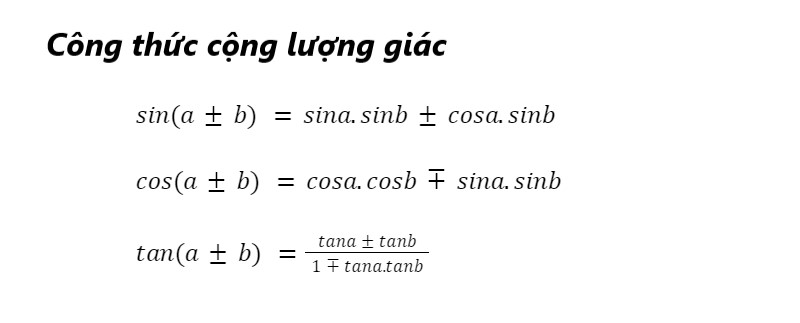
Bảng tổng hợp công thức lượng giác (đầy đủ)
Trong bảng công thức lượng giác từ cơ bản, đến nâng cao, kết hợp với công thức nghiệm của phương trình. Nắm rõ công thức được ứng dụng phổ biến và hiểu rõ cách tính giúp học sinh học toán dễ dàng hơn.Có thể bạn quan tâm Hướng dẫn học công thức biến đổi tích […]

