Trang chủ » Công thức delta, delta phẩy chính xác nhất

Công thức delta, delta phẩy chính xác nhất

Công thức delta là kiến thức quan trọng trong chương trình Toán học lớp 9. Nắm vững những công thức này sẽ giúp bạn giải được cái bài toán từ cơ bản đến nâng cao. Đây cũng là kiến thức trọng tâm trong môn học này.

Có thể bạn quan tâm

Table of Contents

Delta là gì trong toán học?

Trong chương trình Toán học lớp 9, công thức đen-ta (ký hiệu Δ) được sử dụng để biểu thị biệt thức trong phương trình bậc hai. Với từng giá trị của delta có thể kết luận được số nghiệm của phương trình bậc hai. Cụ thể như sau:

Bạn đang xem: Công thức delta, delta phẩy chính xác nhất

Nếu Δ > 0, phương trình có hai nghiệm phân biệt.
Nếu Δ = 0, phương trình có một nghiệm kép.
Nếu Δ < 0, phương trình không có nghiệm thực (vô nghiệm).

Bên cạnh đó, delta còn là ký hiệu cho đường thẳng đối với các lớp toán cao hơn. Ngoài ra, trong bảng chữ cái Hy Lạp delta có ký hiệu là Δ (đối với chữ hoa) và δ (đối với chữ thường).

công thức delta — Tìm hiểu công thức tính delta trong Toán học

Phương trình bậc hai một ẩn là gì?

Phương trình bậc hai một ẩn là phương trình có dạng: ax² + bx + c = 0.

Trong đó:

a ≠ 0
a, b là hệ số của phương trình bậc hai
c là hằng số
x là ẩn của phương trình

Công thức tính delta của phương trình bậc hai một ẩn

Để giải phương trình bậc hai một ẩn, bạn có thể áp dụng công thức nghiệm sau đây:

Nếu Δ < 0, phương trình vô nghiệm.
Nếu Δ = 0, phương trình có nghiệm kép x₁= x₂= -b/2a
Nếu Δ > 0, phương trình có hai nghiệm x₁ và x₂

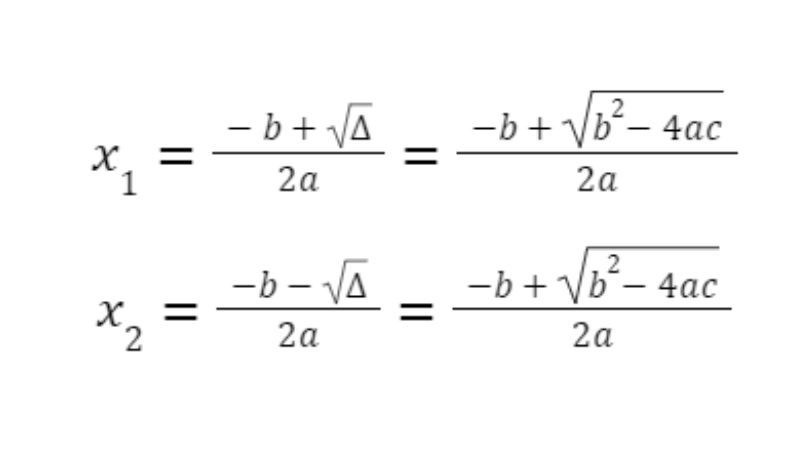
công thức đen ta

Trong phương trình bậc hai một ẩn, công thức tính delta sẽ có dạng như sau:

Ta có phương trình bậc hai: ax²+ bx + c = 0 tính delta Δ = b²– 4ac.

Trong đó:

a, b là hệ số với a ≠ 0
x là ẩn của phương trình
c là hằng số

Công thức tính delta phẩy trong phương trình

Công thức delta phẩy trong phương trình bậc hai ax²+ bx + c = 0 có Δ’ =b’²– ac. Trong đó b’²= b/2 (được gọi là biệt thức delta phẩy).

Nếu Δ’ > 0, phương trình ax²+ bx + c = 0 có hai nghiệm phân biệt.
Nếu Δ’ = 0, phương trình ax²+ bx + c = 0 có nghiệm kép: x₁= x₂= -b’/a.
Nếu Δ’ < 0, phương trình ax²+ bx + c = 0 vô nghiệm.

Tổng quát nghiệm của phương trình bậc hai

Bảng tổng quát về công thức đen-ta và công thức đen-ta phẩy của phương trình bậc hai được tổng hợp chi tiết. Học sinh có thể tham khảo bảng này để biết cách làm và áp dụng vào bài giải môn Toán.

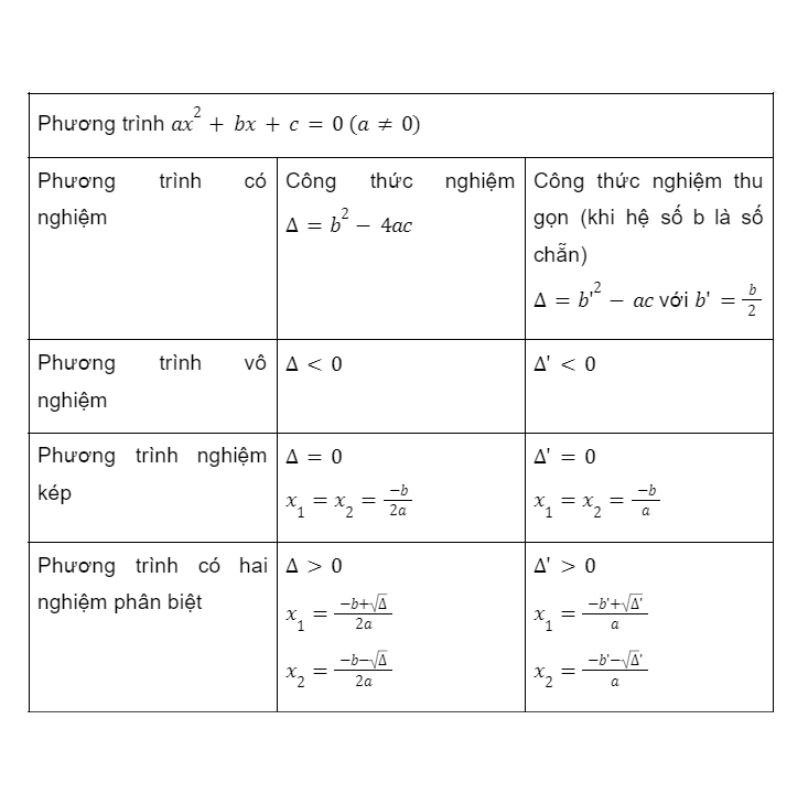
công thức delta phẩy

Bài tập áp dụng công thức delta (có đáp án)

Học sinh có thể áp dụng công thức delta để giải các bài tập phương trình bậc 2 một cách dễ dàng. Bên cạnh đó, bạn cũng có thể sử dụng công thức tính delta bằng bằng máy để cho ra kết quả chính xác và nhanh chóng hơn. Gợi ý một số bài tập cơ bản giúp bạn có thể ôn tập thực hành áp dụng công thức tính.

Bài tập ví dụ

Bài 1: Giải các phương trình sau

6x² + x + 5 = 0
16x² – 40x + 25 = 0
x² – 10x + 21 = 0

Bài 2: Cho phương trình x² – 6x + m² – 4m = 0

Tìm m để phương trình có nghiệm x = 1
Tìm m để phương trình có nghiệm kép
Tìm m để phương trình có hai nghiệm phân biệt

Bài 3: Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải phương trình: 4x² + 4x + 1 = 0

Đáp án tham khảo

Bài 1: Đây là dạng bài tập toán điển hình liên quan đến phương trình bậc hai. Bạn có thể áp dụng công thức nghiệm để giải các phương trình.

a. 6x² + x + 5 = 0

Ta có: Δ = b² – 4ac = 12 – 4.6.5 = 1 – 120 = – 119 < 0

⇒ Phương trình đã cho vô nghiệm.

b. 16x² – 40x + 25 = 0

Ta có: Δ’ = b’2 – ac = (– 20)² – 16.25 = 400 – 400 = 0

⇒ Phương trình đã cho có nghiệm kép:

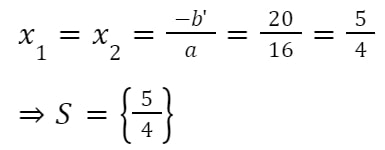
công thức tính đen ta

c. x² – 10x + 21 = 0

Ta có: Δ’ = b’2 – ac = (– 5)2 – 1 . 21 = 25 – 21 = 4 > 0

⇒ Phương trình đã cho có hai nghiệm phân biệt:

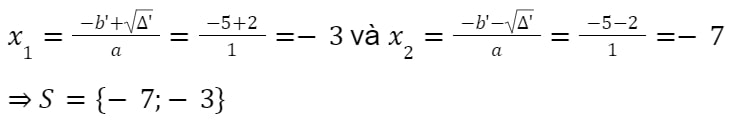
công thức đen ta phẩy

Bài 2: Đây là dạng toán giúp bạn ôn tập công thức tính nghiệm của phương trình.

Gọi phương trình x² – 6x + m² – 4m = 0 là (1)

Với m = 5 hoặc m = -1 thì x = 1 là nghiệm của phương trình (1)
Với m = 2 ± căn 13 thì phương trình (1) có nghiệm kép
Với 2 – căn 13 < m < 2 + căn 13 thì phương trình (1) có hai nghiệm phân biệt

Bài 3: 4x² + 4x + 1 = 0

Ta có: a = 4, b’ = 2, c = 1

⇒ Δ’ = 2² – 4.1 = 0

⇒ Phương trình có nghiệm kép: x₁ = x₂ =-2/4=-1/2

Kết luận

Tổng hợp công thức delta kèm theo ví dụ minh họa giúp học sinh hiểu và biết cách áp dụng vào các bài tập Toán. Việc chủ động ôn tập và rèn luyện kiến thức sẽ giúp bạn đạt được thành tích tốt trong môn học.

Nguồn: https://congthuctoan.com
Danh mục: Đại số