Công Thức Đạo Hàm Nhanh Của Hàm Số Thường Gặp
Nghiên cứu công thức đạo hàm nhanh giúp bạn giải quyết các bài toán nhanh chóng. Với cách nhìn toàn diện về công thức tính nhanh, bạn có thể giải quyết các dạng của hàm số lượng giác, đa thức, mũ logarit.
Công thức đạo hàm nhanh
Công thức tính nhanh đạo hàm là công cụ quan trọng để giải quyết những bài toán giải tích. Tổng hợp các công thức được tổng hợp giúp học sinh giải toán nhanh, chính xác hơn.


Quy tắc tính đạo hàm nhanh
Dùng những quy tắc, công thức cơ bản giúp học sinh giải bài tập nhanh, hiệu quả. Tham khảo một số gợi ý giúp bạn hiểu rõ cách giải quyết mọi đề bài:
| Quy tắc | Chi tiết |
| Cơ bản | Công thức đạo hàm cơ bản: Số lũy thừa, lượng giác, mũ. |
| Chuỗi | Đạo hàm của hàm hợp. Ví dụ: y = (x^2 + 1)^3 có đạo hàm là 3(x^2 + 1)^2 x 2x. |
| Tích và thương | Tính đạo hàm của tích hoặc thương hàm số, ví dụ đạo hàm u’v là (u’v + uv’). |
Mẹo giải đạo hàm trên máy tính cầm tay
Dùng máy tính cầm tay giúp tính toán đạo hàm nhanh hơn. Học sinh có thể vận dụng công cụ này để giải các đề bài:
-
-
- Chế độ tính: Đối với máy Casio cài sẵn chế độ COMPUTE.
- Tính năng Derivative: Dùng máy tính Casio fx 880 BTG giúp tính đạo hàm tại điểm cụ thể. Bạn chỉ cần nhập hàm, giá trị của biến để nhận kết quả nhanh.
- Tạo bảng giá trị: Tạo bảng này để giải những hàm phức tạp, tạo giá trị xem cách thay đổi hàm số để tìm ra đạo hàm tại các điểm cụ thể.
- Check lại lỗi: Dùng tính năng kiểm tra lỗi của máy để xem xét có sai khi nhập dữ liệu vào không.
-

Mặc dù có máy tính hỗ trợ để giải bài toán đạo hàm, nhưng không thể thay thế hoàn toàn được. Bạn vẫn phải nắm rõ các công thức tính nhanh, áp dụng các quy tắc và phương pháp tính.
Giải đáp các thắc mắc khi giải toán đạo hàm
Một số thắc mắc liên quan đến công thức đạo hàm nhanh có thể giúp bạn học tốt, giải bài dễ dàng hơn.
1. Đạo hàm là gì?
Đạo hàm là hàm số tại một điểm cho biết tỷ lệ thay đổi tức thời của hàm số tại điểm đó. Đạo hàm chính là cơ sở của giải tích, xác định tốc độ thay đổi, độ dốc của đường tiếp tuyến và các đặc điểm khác trên đồ thị.
2. Làm sao để tính đạo hàm hàm số?
Bạn có thể tính đạo hàm theo quy tắc hàm số lượng giác, chuỗi và tích. Từng quy tắc có ứng dụng riêng, học sinh có thể căn cứ vào từng trường hợp để giải bài.
3. Hàm số không có đạo hàm trong trường hợp nào?
Hàm số không có đạo hàm trong các trường hợp:
-
-
- Tại những điểm mà tại đó hàm số không liên tục.
- Tại những điểm có góc cạnh.
- Ở điểm gấp khúc.
- Điểm có dạng đặc biệt khác.
-
4. Vì sao phải đạo hàm?
Đạo hàm là công cụ giúp giải toán và ứng dụng trong nhiều lĩnh vực khác nhau gồm:
-
-
- Khoa học
- Kỹ thuật
- Kinh tế.
-
Kết luận
Xác định công thức đạo hàm nhanh giúp học sinh có thể giải toán dễ dàng và chuẩn xác hơn. Bạn có thể xác định các loại chuỗi và căn cứ vào từng trường hợp để tìm ra cách giải theo đề bài được đưa ra.
Nguồn: https://congthuctoan.com
Danh mục: Giải tích
Bài viết liên quan

Các công thức số phức và phương pháp giải toán từ cơ bản đến nâng cao
Tìm hiểu các công thức số phức từ cơ bản đến nâng cao với phương pháp giải chi tiết, dễ hiểu. Bao gồm dạng đại số, lượng giác và ứng dụng trong hình học, vật lý điện học.

Khám phá công thức lim và phương pháp tính giới hạn hàm số cơ bản
Tìm hiểu các công thức lim từ cơ bản đến nâng cao với phương pháp giải chi tiết. Hướng dẫn tính lim một phía, lim vô cùng và xử lý dạng vô định kèm bài tập mẫu dễ hiểu.

Tìm hiểu công thức tích phân từng phần và phương pháp giải chi tiết
Tìm hiểu chi tiết công thức tích phân từng phần với phương pháp udv đơn giản, dễ hiểu. Hướng dẫn cách tính, các dạng bài tập thường gặp kèm lời giải cụ thể cho học sinh.

Công thức tích phân đầy đủ Và chính xác nhất
Khám phá công thức tích phân giúp bạn tiếp cận môn toán học dễ dàng hơn. Khái niệm này được ứng dụng trong nhiều lĩnh vực trong đời sống, có liên quan đến tính diện tích, khối lượng, tỉ suất thay đổi một lượng hoặc đạo hàm của hàm số.Có thể bạn quan tâm Công […]

Công Thức Nguyên Hàm Đầy Đủ Và Chính Xác Nhất
Nắm công thức nguyên hàm giúp học sinh có thể làm bài tập và vượt qua bài thi dễ dàng hơn. Kiến thức này khá rộng và tạo thử thách lớn, đòi hỏi bạn phải tìm hiểu kỹ để nắm được cách giải bài tập chuẩn hơn.Có thể bạn quan tâm Khám phá công thức […]
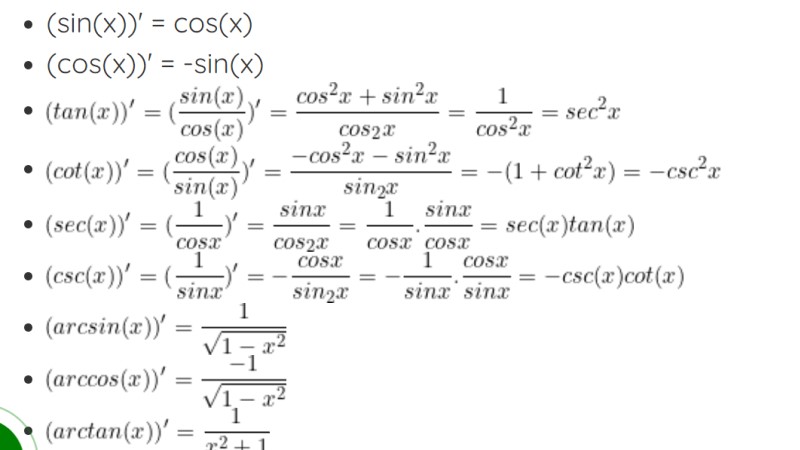
Tổng hợp công thức đạo hàm cơ bản đầy đủ nhất
Nắm công thức đạo hàm và đạo hàm lượng giác giúp bạn tổng hợp và nắm kiến thức đầy đủ hơn. Học theo bảng tổng hợp, bạn có thể giải bài tập dễ dàng, ứng dụng hiệu quả trong quá trình giải toán.Có thể bạn quan tâm Công thức tích phân đầy đủ Và chính […]

