Tổng hợp công thức đạo hàm cơ bản đầy đủ nhất 

Nắm công thức đạo hàm và đạo hàm lượng giác giúp bạn tổng hợp và nắm kiến thức đầy đủ hơn. Học theo bảng tổng hợp, bạn có thể giải bài tập dễ dàng, ứng dụng hiệu quả trong quá trình giải toán.

Đạo hàm là gì?

Đạo hàm là đại lượng thể hiện sự biến thiên của hàm tại điểm nào đó. Trong đó, chiều biến thiên lên hay xuống của hàm sôs là giá trị đạo hàm. Yếu tố này đóng vai trò quan trọng trong lĩnh vực vật lý, toán hình học và không gian.

Bạn đang xem: Tổng hợp công thức đạo hàm cơ bản đầy đủ nhất 

Ta có hàm số: y = f(x) được xác định trong khoảng (a;b):

• Điểm x0 thuộc khoảng (a;b)
• Giới hạn hữu hạn (Xét trường hợp có nghĩa) của tỉ số khi x đến x0 là đạo hàm tại điểm x0.
• Ký hiệu đạo hàm: f’(x) hay y’(x).

Quy tắc tính đạo hàm

Khi muốn tính đạo hàm, bạn có thể thực hiện theo các bước:

• Bước 1: Đặt dx là gia số của x tại x0, ta có y = f(x0 – x) – f(x0).
• Bước 2: Lập tỷ số dy/dx.
• Bước 3: Tính giới hạn dy/dx khi dx đến 0: lim (dx->d0) của dy/dx.

Khi thay x0 = x, ta có hàm số y = f(x), với x thuộc khoảng (a;b).

Bảng công thức đạo hàm đầy đủ nhất

Các công thức đạo hàm cơ bản gồm: Đa thức, phân thức hữu tỉ, hàm số căn bậc hai, lũy thừa, mũ, logarit, đạo hàm hàm số lượng giác,… Học sinh cần học đầy đủ các công thức để giải bài tập chính xác, đem lại kết quả tốt.

Công thức đạo hàm số thường gặp

Đạo hàm của hàm số cơ bản và đạo hàm hàm số lượng giác là những công thức thường gặp nhất. Tham khảo công thức chi tiết:

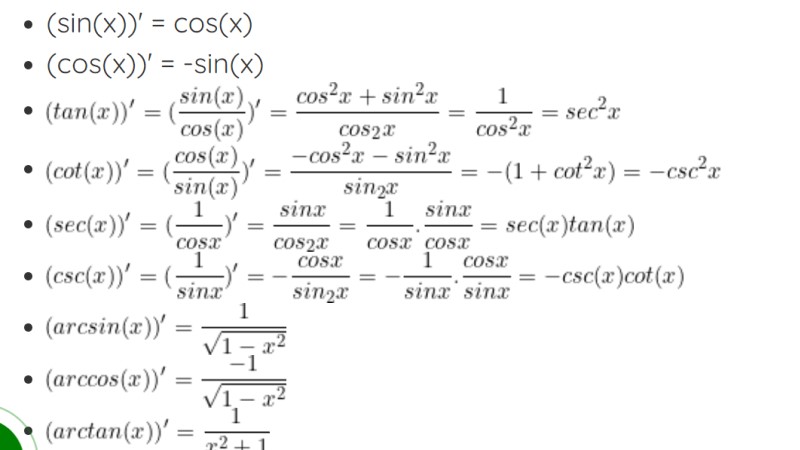
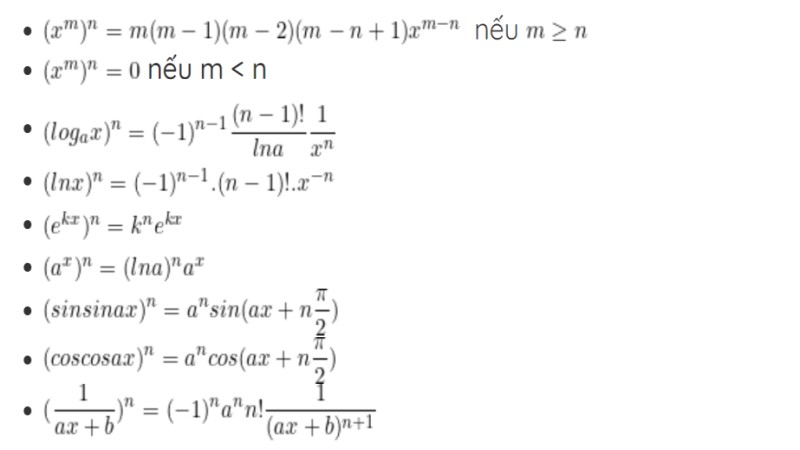
Các mẫu bài tập tính đạo hàm thường gặp

Trong quá trình học và giải bài tập, cần lưu ý về các hình thức ra đề. Mỗi dạng có đặc điểm và cách giải riêng.

Dạng 1: Tính đạo hàm từ định nghĩa

Dạng này cơ bản nhất, giúp học sinh nắm rõ lý thuyết và phương pháp giải. Bạn cần căn cứ vào định nghĩa rồi áp dụng công thức tính toán tương ứng.

Dạng 2: Chứng minh đẳng thức liên quan đạo hàm

Học sinh cần chứng minh những hệ thức được đưa ra (Theo điều kiện có sẵn) có liên quan đến đạo hàm. Quá trình tính toán và chứng minh phải đảm bảo sự chính xác để đưa ra kết quả.

Dạng 3: Viết phương trình tiếp tuyến khi biết tiếp điểm

Xem thêm : Khám phá công thức lim và phương pháp tính giới hạn hàm số cơ bản

Dạng bài tập này đưa ra phương trình tiếp tuyến của hàm số một đường cong (C) dạng: y = f(x), tiếp điểm M(x0;y0) dạng y = y’(x0)(x-x0) + y0.

Ví dụ: Cho hàm số y = x^3 + 3mx^2 + (m+1)x + 1(1), m là tham số thực. Tìm giá trị của m để tiếp tuyến đồ thị hàm số tại điểm có hoành độ x = -1 qua điểm B(1;2).

Giải bài:

Tập xác định D = R.

y’ = f’(x) = 3 x 2 + 6mx + m + 1

Ta có x0 = -1

=> y0 = 2m – 1, f’(-1) = -5m + 4

Phương trình tiếp tuyến tại M(-1;2m-1): y = (-5m + 4)(x + 1) + 2m – 1 (d).

Đường tiếp tuyến đi qua điểm B nên ta có: (-5m + 4)x2 + 2m – 1= 2 => m = 5/8.

Với m = 5/8, tiếp tuyến đồ thị có hoành độ x = -1, đi qua điểm B(1;2).

Dạng 4: Viết phương trình tiếp tuyến đã biết hệ số góc

Bài tập này yêu cầu viết phương trình tiếp tuyến của (C): y = f(x) có hệ số góc là k.

Dạng 5: Phương trình. bất phương trình có đạo hàm

Bài tập được đưa ra theo dạng này yêu cầu kết hợp nhiều công thức đạo hàm và nguyên hàm. Từ đó, bạn có thể giải phương trình hoặc bất phương trình để tìm ra kết quả.

Dạng 6: Áp dụng công thức đạo hàm của nguyên hàm

Xem thêm : Công Thức Đạo Hàm Nhanh Của Hàm Số Thường Gặp 

Dạng đề này đòi hỏi người giải hiểu rõ bản chất, công thức tính đạo hàm. Nếu đề ra những hàm số phức tạp, học sinh có thể rút gọn hàm số, sau đó làm đạo hàm.

Dạng 7: Tính đạo hàm cấp cao

Đề bài này thường yêu cầu học sinh tính đạo hàm cấp 2, bạn cần áp dụng công thức đạo hàm cấp 2. Bạn có thể dùng công thức đạo hàm cấp cao, hoặc dùng y(n) = (y(n-1))’.

Lưu ý: Muốn tính đạo hàm cấp n, cần xem lần lượt đạo hàm cấp 1, 2, 3,… lần lượt rồi suy luận đạo hàm cấp n.

Giải bài tập liên quan đến công thức tính đạo hàm

Từ bảng công thức đạo hàm, học sinh có thể giải các bài tập dễ dàng. Một số ví dụ tham khảo đơn giản nhất sẽ giúp bạn hình dung được cách chính xác.

1. Tính đạo hàm của hàm số được đưa ra:

Bạn dựa vào đề bài được đưa ra và hoàn thành phép tính.

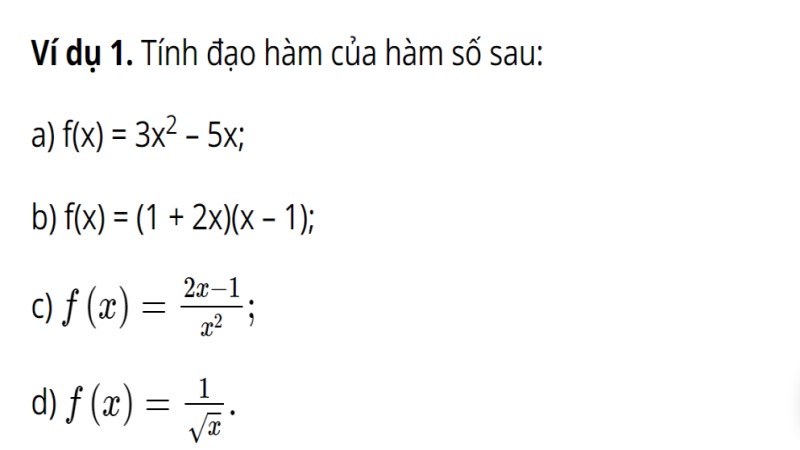
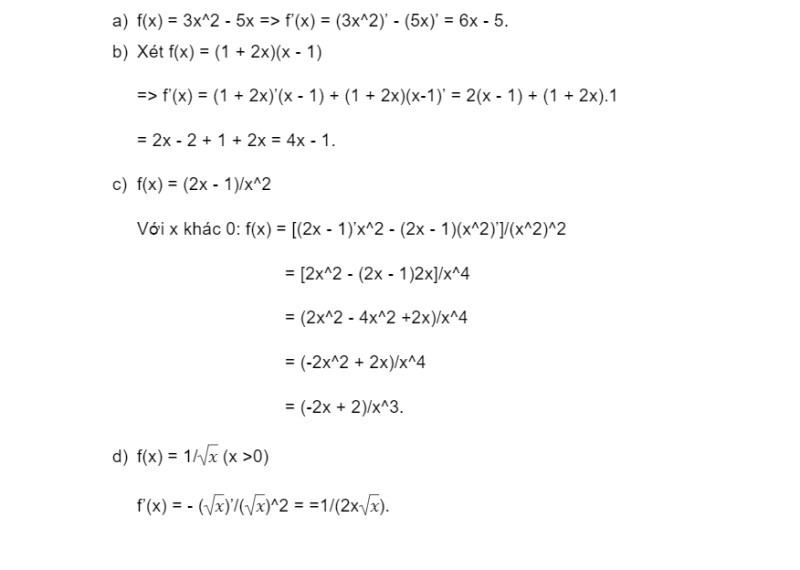
2. Giải bài tập tính đạo hàm công thức

Bạn làm bài tập tính đạo hàm các số theo hình đề bài.

Cách giải chi tiết:

1. y’ = (sinx)’ – ½(cosx)’ = cosx + 1/2sinx.
2. y’ = (tanx)’ – 1/(cotx)’ = 1/cos^2(x) + 1/sin^2(x).
3. y’ = [(sinx)’sinxcosx – sinx(sinxcosx)’]/(sinxcosx)^2.

= {cosxsinxcosx – sinx[cos^2(x) – sin^2(x)]}/sin^2(x)cos^2(x)

= [cos^2(x) – cos^2(x) + sin^2(x)]/sinxcos^2(x) = sin^2(x)/sinxcos^2(x)

= sinx/cos^2(x).

Kết luận

Hiểu rõ công thức đạo hàm và nắm được các dạng bài tập giúp bạn tìm ra hướng giải chuẩn xác hơn. Đây là thử thách của nhiều học sinh, cần phải luyện tập nhiều để hiểu rõ bản chất của đề bài.

Nguồn: https://congthuctoan.com
Danh mục: Giải tích