Tổng hợp công thức cấp số cộng và phương pháp giải bài tập chi tiết nhất
Thầy hướng dẫn chi tiết các công thức cấp số cộng cùng phương pháp giải bài tập từ cơ bản đến nâng cao. Bài giảng được thiết kế đặc biệt với nhiều ví dụ minh họa sinh động, giúp học sinh yếu toán dễ dàng nắm vững kiến thức và áp dụng thành thạo vào giải các dạng bài tập khác nhau.
Cấp số cộng là gì?
Cấp số cộng là một dãy số mà mỗi số hạng (trừ số hạng đầu tiên) bằng số hạng liền trước cộng với một số không đổi. Số không đổi đó được gọi là công sai của cấp số cộng. Ví dụ: dãy số 2, 5, 8, 11, 14,… là một cấp số cộng với công sai d = 3.
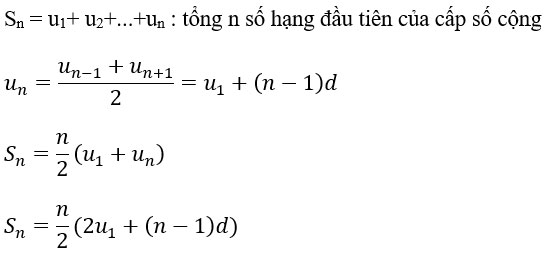
Để hiểu rõ hơn về công thức cấp số cộng là gì, ta cần nắm vững các yếu tố cơ bản. Một cấp số cộng được xác định bởi số hạng đầu tiên (a₁), công sai (d) và số lượng số hạng (n). Từ đó, ta có thể tính được số hạng thứ n theo công thức:
aₙ = a₁ + (n-1)d.
Một điểm quan trọng khi học về cấp số cộng là tổng của n số hạng đầu tiên. Tổng này có thể tính bằng công thức tính trung bình cộng của số hạng đầu và số hạng cuối nhân với số lượng số hạng. Điều này giúp ta giải quyết nhiều bài toán thực tế như tính lương tăng theo thâm niên hay tính khoảng cách di chuyển đều.
Khi áp dụng cấp số cộng vào thực tế, ta thường gặp các ví dụ như: một công nhân năm đầu tiên nhận lương 5 triệu đồng, mỗi năm được tăng 500 nghìn đồng. Đây chính là một cấp số cộng với số hạng đầu a₁ = 5 triệu và công sai d = 0,5 triệu.
Các công thức quan trọng trong cấp số cộng
Cấp số cộng là dãy số mà hiệu hai số hạng liên tiếp bằng một số không đổi. Để giải các bài toán về cấp số cộng, việc nắm vững các công thức cấp số cộng là vô cùng quan trọng. Tôi sẽ giúp các em hiểu rõ từng công thức một cách đơn giản nhất.
Công thức tính số hạng thứ n của cấp số cộng
Khi biết số hạng đầu tiên (a₁) và công sai (d), ta có thể tính được công thức tính số số hạng thứ n theo công thức: aₙ = a₁ + (n-1)d. Công thức này giống như việc ta đi từng bước một, mỗi bước cách nhau một khoảng bằng d, và đi tổng cộng (n-1) bước từ điểm xuất phát a₁.

Công thức tính công sai trong cấp số cộng
Công thức tính công sai d = (aₙ – a₁)/(n-1) được sử dụng khi ta biết số hạng đầu tiên và một số hạng bất kỳ thứ n. Giống như việc tính tốc độ trung bình, ta lấy quãng đường đi được (aₙ – a₁) chia cho số bước đi (n-1).
Công thức tính tổng n số hạng đầu tiên
Để tính tổng n số hạng đầu tiên của cấp số cộng, ta sử dụng công thức
Sₙ = (n/2)(a₁ + aₙ)
Công thức này có thể kết hợp với công thức lũy thừa trong một số trường hợp phức tạp hơn.
Ví dụ minh họa về cách áp dụng công thức
Giả sử ta có một cấp số cộng với a₁ = 3, d = 2. Tìm số hạng thứ 5 và tổng 5 số hạng đầu tiên.
Bước 1: Tính a₅ = a₁ + (5-1)d = 3 + 4×2 = 11
Bước 2: Tính S₅ = (5/2)(3 + 11) = 35
Qua ví dụ trên, ta thấy việc áp dụng công thức rất đơn giản nếu nắm vững các bước tính toán cơ bản.
Hướng dẫn giải các dạng bài tập cơ bản về cấp số cộng
Cấp số cộng là một dãy số mà hiệu hai số hạng liên tiếp bất kỳ bằng một hằng số. Để giải các bài tập về cấp số cộng, chúng ta cần nắm vững các công thức cơ bản và phương pháp giải phù hợp.

Bài tập tìm số hạng đầu và công sai
Phương pháp giải và ví dụ minh họa
Để tìm được số hạng đầu và công sai của một cấp số cộng, ta cần xác định mối quan hệ giữa các số hạng. Cách tìm số hạng đầu cấp số cộng thường dựa vào các số hạng đã biết và vị trí của chúng trong dãy số.
Ví dụ: Cho cấp số cộng có số hạng thứ 3 là 11 và số hạng thứ 6 là 20. Tìm số hạng đầu tiên và công sai.
Giải:
– Gọi a là số hạng đầu, d là công sai
– u3 = a + 2d = 11
– u6 = a + 5d = 20
– Từ đó: 20 – 11 = 3d → d = 3
– Thay d = 3 vào u3 = a + 2d → a = 5
Bài tập tính tổng cấp số cộng
Các bước giải chi tiết kèm ví dụ
Cách tìm công sai cấp số cộng là bước quan trọng trước khi tính tổng. Sau khi có công sai, ta áp dụng công thức tính tổng dãy số để tìm kết quả.
Ví dụ: Tính tổng cấp số cộng có số hạng đầu là 2, công sai là 3 và số hạng cuối là 20.
Giải:
– Số hạng đầu a = 2
– Công sai d = 3
– Số hạng cuối un = 20
– Tìm n: 20 = 2 + (n-1)3 → n = 7
– Áp dụng công thức tổng: Sn = (a1 + an)×n/2
– S7 = (2 + 20)×7/2 = 77
Kết quả thu được giúp học sinh dễ dàng kiểm chứng bằng cách cộng trực tiếp các số hạng: 2 + 5 + 8 + 11 + 14 + 17 + 20 = 77.
Các dạng bài tập nâng cao và cách giải
Khi học về cấp số cộng, việc nắm vững các dạng bài tập khác nhau sẽ giúp học sinh phát triển tư duy toán học và áp dụng linh hoạt vào thực tế. Tôi sẽ phân tích chi tiết từng dạng bài tập phổ biến cùng phương pháp giải quyết hiệu quả.
Bài tập về số hạng tổng quát của cấp số cộng
Dạng bài tập cấp số cộng về số hạng tổng quát thường yêu cầu tìm công thức tổng quát Un hoặc xác định các yếu tố như số hạng đầu a1, công sai d. Để giải dạng bài này, cần áp dụng công thức Un = a1 + (n-1)d kết hợp với các điều kiện đã cho. Tương tự như khi học về công thức số phức, việc nắm chắc công thức cơ bản là nền tảng quan trọng.
Bài tập về tổng các số hạng đặc biệt
Các ví dụ cấp số cộng về tổng thường xuất hiện dưới dạng tính tổng các số hạng liên tiếp hoặc số hạng có vị trí đặc biệt. Phương pháp giải cần dựa vào công thức tổng n số hạng đầu tiên:
Sn = n(a1 + an)/2 hoặc Sn = n[2a1 + (n-1)d]/2.
Ví dụ minh họa chi tiết
Một bài toán điển hình trong cấp số cộng trong đề thi như sau:
Cho cấp số cộng (un) có u1 = 2 và u5 = 14. Tính tổng 10 số hạng đầu tiên của dãy.

Cách giải:
- Tìm công sai d:
u5 = u1 + 4d = 14
2 + 4d = 14
d = 3
- Tính u10:
u10 = 2 + 9×3 = 29
- Áp dụng công thức tổng:
S10 = 10(2 + 29)/2 = 155
FAQ: Câu hỏi thường gặp về cấp số cộng
Khi học về công thức cấp số cộng, nhiều học sinh thường gặp những thắc mắc và khó khăn. Tôi sẽ giải đáp một số câu hỏi phổ biến nhất sau 30 năm giảng dạy môn toán.
Làm sao để nhận biết một dãy số là cấp số cộng?
Để nhận biết một dãy số có phải cấp số cộng hay không, ta chỉ cần lấy số hạng sau trừ số hạng trước liên tiếp. Nếu các hiệu bằng nhau thì đó là cấp số cộng. Ví dụ: Dãy số 2, 5, 8, 11, 14 có hiệu các số liên tiếp đều là 3, vậy đây là cấp số cộng với công sai d = 3.
Có những phương pháp nào để ghi nhớ công thức cấp số cộng?
Một cách đơn giản để ghi nhớ công thức csc là liên hệ với thực tế. Tưởng tượng bạn đi lên cầu thang, mỗi bước bạn bước lên một khoảng cách bằng nhau – đó chính là công sai d. Số bước bạn đi là n, và vị trí ban đầu là số hạng đầu tiên a₁. Với cách liên tưởng này, công thức tổng quát aₙ = a₁ + (n-1)d sẽ dễ nhớ hơn rất nhiều.
Cách kiểm tra kết quả bài toán cấp số cộng
Phương pháp kiểm tra kết quả đơn giản nhất là thay ngược kết quả vào điều kiện đề bài. Nếu là bài tìm số hạng thứ n, hãy kiểm tra xem số hạng tìm được có tạo thành cấp số cộng với các số hạng đã cho không. Với bài tìm tổng, có thể chia đôi dãy số và cộng các cặp số đối xứng – tổng các cặp phải bằng nhau.
Các kiến thức về **công thức cấp số cộng** đóng vai trò nền tảng trong chương trình toán học phổ thông. Việc nắm vững các công thức tính số hạng, công sai và tổng của dãy số giúp học sinh giải quyết nhiều bài toán thực tế. Thông qua các ví dụ minh họa và phương pháp giải chi tiết, các em có thể áp dụng linh hoạt kiến thức này vào các dạng bài tập từ cơ bản đến nâng cao.
Nguồn: https://congthuctoan.com
Danh mục: Đại số
Bài viết liên quan

Công thức số mũ và các quy tắc tính toán cơ bản trong toán học
Tìm hiểu chi tiết các công thức số mũ từ cơ bản đến nâng cao với cách giải thích đơn giản. Bao gồm quy tắc tính toán, mối quan hệ với căn thức, logarit và ứng dụng thực tế.

Công thức nghiệm pt bậc 2 và cách giải đơn giản cho học sinh yếu
Tìm hiểu chi tiết công thức nghiệm pt bậc 2 với cách giải đơn giản, dễ hiểu. Bao gồm công thức delta, phân loại nghiệm và phương pháp giải kèm bài tập mẫu có lời giải.

Tổng hợp công thức tổng hiệu và cách tính tổng dãy số cơ bản
Tìm hiểu các công thức tổng hiệu từ cơ bản đến nâng cao trong toán học. Hướng dẫn chi tiết cách tính tổng dãy số, tổng bình phương, cấp số cộng và các dãy số đặc biệt kèm bài tập mẫu.

Tổng hợp công thức hằng đẳng thức cơ bản và nâng cao chi tiết nhất
Tìm hiểu các công thức hằng đẳng thức từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập mẫu. Tổng hợp đầy đủ các dạng hằng đẳng thức quan trọng trong chương trình toán phổ thông.

Công thức logarit cơ bản và nâng cao dành cho học sinh yếu toán
Tìm hiểu các công thức logarit từ cơ bản đến nâng cao với cách giải thích đơn giản, dễ hiểu. Bao gồm công thức log, đạo hàm, tích phân kèm bài tập mẫu và ứng dụng thực tế.

Tổng hợp công thức lũy thừa và áp dụng giải bài tập đơn giản
Tìm hiểu các công thức lũy thừa từ cơ bản đến nâng cao với cách giải thích đơn giản, dễ hiểu. Bao gồm quy tắc, tính chất và bài tập mẫu chi tiết cho học sinh phổ thông.

