Hướng dẫn học công thức biến đổi tích thành tổng và bài tập
Công thức biến đổi tích thành tổng nằm trong các công thức lượng giác nhất định phải nhớ. Nắm vững kiến thức này giúp bạn đơn giản hoá các bài tập toán học và đạt điểm cao.
Giải thích công thức biến đổi tích thành tổng là gì?
Công thức tích thành tổng dùng để biến đổi biểu thức tích của hàm lượng giác thành tổng hiệu sao cho giảm đi tính phức tạp. Muốn giải toán nhanh phải hiểu được bản chất vấn đề nên bạn cần hiểu sâu ý nghĩa của nó.

Tính ứng dụng của công thức này rất cao nên bạn cần nắm vững, chăm chỉ làm bài tập. Các hàm lượng giác chiếm số điểm không thấp trong đề kiểm tra trên lớp và đề thi đại học nên đừng lơ là.
Thông thường, công thức này sẽ liên quan đến Sin và Cos. Từ tích ban đầu đổi thành các tổng và các hiệu cụ thể như sau:
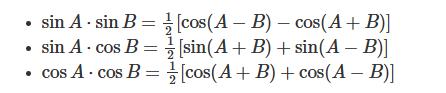
Trong đó:
- Hàng đầu tiên là công thức tích của hai hàm sin.
- Hàng thứ hai là tích hàm sin và cos.
- Hàng thứ ba là công thức tích hai hàm cos.
Để hiểu hơn về cách biến đổi tích thành tổng, bạn có thể tham khảo bài tập đơn giản dưới đây.
Đề bài: Biến đổi biểu thức và tính giá trị biểu thức 2sin(a).cos(b) với a = π/4 và b = π/3.
Cách giải:
Từ công thức ở trên có thể biến đổi 2sin(a).cos(b) = sin (a+b) + sin (a-b). Khi thay số vào tính giá trị sẽ có 2sin(π/4).cos(π/3) = sin 7π/12 + sin π/12 rất dễ hiểu.
Ứng dụng của hàm lượng giác trong thực tế như thế nào?
Nhiều người có nhận định rằng các công thức toán học phức tạp chẳng mang đến lợi ích gì trong cuộc sống. Nhưng thực ra chúng là một trong những yếu tố quan trọng để phát triển công nghệ.
Với công thức biến đổi tích thành tổng, một số ứng dụng phổ biến nhất là:
- Đơn giản hoá hàm số lượng giác: Bài tập áp dụng thường thấy nhất là đạo hàm và tích phân giúp giảm thiểu đi tính dài dòng và phức tạp.
- Giải hình học không gian: Tưởng chừng không liên quan nhưng thực chất các công thức lượng giác có thể giúp tính góc, tính khoảng cách giữa các điểm.
- Ứng dụng trong kỹ thuật điện: Phổ biến nhất chính là việc nghiên cứu để tạo ra các mạch điện. Tính được điện áp sẽ giúp thiết kế mạch xoay chiều chính xác, sử dụng hiệu quả.
- Sóng âm: Công thức toán còn có tác dụng với việc phát triển các định nghĩa vật lý. Từ việc biến sóng âm phức tạp thành đơn giản có thể xử lý âm thanh tốt hơn. Chuyên gia còn có thể tạo nên các hiệu ứng đặc biệt.

Hướng dẫn cách ghi nhớ nhanh công thức lượng giác
Sin hay Cos đều không phải những từ thường gặp trong cuộc sống mà chỉ thấy khi học tập. Thế nên nếu muốn ghi nhớ thì bạn cần phải tạo cho mình một cách học riêng, tránh thuộc vẹt và không biết áp dụng.
Cách nhiều người áp dụng nhất là phổ thành thơ để có nhịp điệu cho dễ nhớ. Bạn có thể học thuộc bài thơ biến đổi tích thành tổng trong lượng giác như sau:
“Cos cos nửa cos, cos cộng cộng cos trừ
Sin sin nửa cos, trừ cos cộng trừ cos trừ
Sin cos nửa sin, sin cộng cộng sin trừ”.
Bài tập về công thức tích thành tổng và lời giải
Khi đã thuộc được cách biến đổi rồi thì bạn có thể áp dụng vào bài tập toán Đại số của mình. Thông thường đề sẽ ra theo dạng yêu cầu bạn tính giá trị biểu thức với đơn vị là π.
Chẳng hạn ta có:
Đề 1: Tính giá trị của B = sin(15π/27).sin(6π/27)
=> Cách giải: Áp dụng công thức biến đổi tích thành tổng để có được:
B = 1/2[cos(15π/27-6π/27) – cos(15π/27+6π/27)
= 1/2(cosπ/3 – cos7π/9)
Sau đó tính giá trị cụ thể là ra đáp án cuối cùng của biểu thức B.
Công thức tổng thành tích và tích thành tổng khác nhau thế nào?
Công thức biến đổi tổng thành tích ngược lại với tích thành tổng. Nghĩa là từ hàm Sin, Cos tổng ban đầu bạn đổi thành tích để mục đích tạo ra sự liên kết giữa các thành phần và rút gọn, tính giá trị biểu thức dễ hơn.

Công thức này có dạng là:

Ví dụ dễ hiểu:
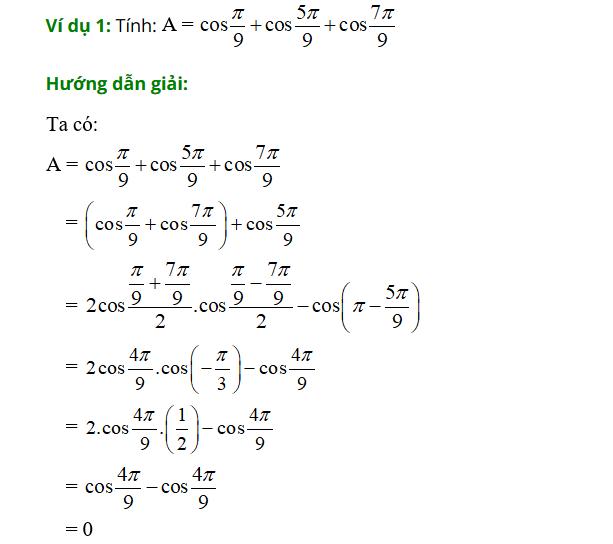
Kết luận
Học công thức biến đổi tích thành tổng và áp dụng đúng cách không dễ nhưng cũng không tới mức quá khó nếu bạn chăm chỉ. Bạn hãy tham khảo mẹo học thuộc được gợi ý và bài tập thường xuyên để rèn luyện.
Nguồn: https://congthuctoan.com
Danh mục: Lượng giác
Bài viết liên quan

Công thức hạ bậc là gì? Tổng hợp công thức hạ bậc lượng giác
Công thức hạ bậc là một trong những khái niệm quan trọng bậc nhất của bộ môn Lượng giác. Nắm vững kiến thức này giúp bạn nhanh chóng giải được các bài về tích phân cũng như các phương trình phức tạp.Có thể bạn quan tâm Hướng dẫn học công thức biến đổi tích thành […]

Công thức hệ thức lượng Thức Hệ Thức Lượng Tam Giác Lượng
Nghiên cứu công thức hệ thức lượng trong tam giác vuông được ứng dụng theo nguyên lý cơ bản đến phức tạp. Phép tính được thực hiện và ứng dụng nhiều trong toán hình học, cũng như nhiều lĩnh vực trong thực tiễn.Có thể bạn quan tâm Công thức hạ bậc là gì? Tổng hợp […]
Bảng tổng hợp công thức lượng giác (đầy đủ)
Trong bảng công thức lượng giác từ cơ bản, đến nâng cao, kết hợp với công thức nghiệm của phương trình. Nắm rõ công thức được ứng dụng phổ biến và hiểu rõ cách tính giúp học sinh học toán dễ dàng hơn.Có thể bạn quan tâm Công thức hệ thức lượng Thức Hệ Thức […]

