Lý thuyết công thức Bernoulli và các ứng dụng trong toán học phổ thông

Thầy giáo toán với hơn 30 năm kinh nghiệm giảng dạy sẽ hướng dẫn chi tiết về **công thức Bernoulli** qua các ví dụ thực tế đơn giản. Bài viết phân tích rõ ràng cách áp dụng công thức trong toán học và vật lý, kèm theo phương pháp giải các dạng bài tập từ cơ bản đến nâng cao dành cho học sinh trung học phổ thông.

Công thức Bernoulli là gì và ý nghĩa trong toán học?

Công thức bernoulli là gì – đây là một công thức toán học quan trọng được phát minh bởi nhà toán học Jacob Bernoulli vào thế kỷ 17. Công thức này mô tả mối quan hệ giữa xác suất thành công và thất bại trong một chuỗi các phép thử độc lập.

Bạn đang xem: Lý thuyết công thức Bernoulli và các ứng dụng trong toán học phổ thông

Khi nói đến bernoulli toán là gì, chúng ta có thể hiểu đơn giản như sau: Nếu bạn tung một đồng xu công bằng nhiều lần, xác suất để được mặt ngửa trong mỗi lần tung là như nhau và độc lập với các lần tung trước đó. Đây chính là một ví dụ điển hình về phép thử Bernoulli.

Công thức Bernoulli được biểu diễn như sau:

P(X = k) = C(n,k) × p^k × (1-p)^(n-k)

Trong đó:
– n là số lần thử
– k là số lần thành công
– p là xác suất thành công của mỗi lần thử
– C(n,k) là tổ hợp chập k của n phần tử

Ví dụ thực tế: Một học sinh làm bài trắc nghiệm 5 câu, mỗi câu có 4 đáp án. Em này chọn ngẫu nhiên các đáp án. Xác suất để em đó trả lời đúng 3 câu sẽ được tính bằng công thức Bernoulli với n=5, k=3, p=1/4.

Công thức Bernoulli có ý nghĩa to lớn trong thống kê và xác suất. Nó giúp các nhà khoa học dự đoán kết quả của các thí nghiệm lặp đi lặp lại, từ đó đưa ra những quyết định quan trọng trong nghiên cứu và sản xuất.

Các dạng biểu diễn và chứng minh công thức Bernoulli

Công thức Bernoulli là một công thức quan trọng trong giải tích, giúp tính toán các biểu thức có dạng (1+x)^n. Công thức có nhiều ứng dụng trong toán học và các lĩnh vực khác như xác suất thống kê, tài chính. Tương tự như cách biểu diễn số phức dạng đại số, công thức Bernoulli cũng có nhiều dạng biểu diễn khác nhau.

Biểu diễn toán học của công thức Bernoulli

Công thức Bernoulli có dạng tổng quát:

(1+x)^n = C(n,0) + C(n,1)x + C(n,2)x^2 + … + C(n,n)x^n

Trong đó:
– n là số mũ nguyên dương
– x là biến số
– C(n,k) là tổ hợp chập k của n phần tử

Chứng minh công thức Bernoulli bằng phương pháp quy nạp

Công thức Bernoulli chứng minh được thực hiện qua các bước sau:

Bước 1: Kiểm tra công thức đúng với n = 1
(1+x)^1 = 1 + x = C(1,0) + C(1,1)x

Bước 2: Giả sử công thức đúng với n = k
(1+x)^k = C(k,0) + C(k,1)x + C(k,2)x^2 + … + C(k,k)x^k

Bước 3: Chứng minh công thức đúng với n = k+1 bằng cách nhân cả hai vế với (1+x)

Ví dụ minh họa cách áp dụng công thức

Xem thêm : Hướng dẫn công thức tổ hợp và chỉnh hợp cho học sinh trung học phổ thông

Ví dụ: Khai triển (1+x)^4

Áp dụng công thức ta có:
(1+x)^4 = C(4,0) + C(4,1)x + C(4,2)x^2 + C(4,3)x^3 + C(4,4)x^4
= 1 + 4x + 6x^2 + 4x^3 + x^4

Kết quả trên cho thấy hệ số của các số hạng chính là các tổ hợp tương ứng, giúp việc tính toán trở nên đơn giản và nhanh chóng hơn.

Ứng dụng của công thức Bernoulli trong các lĩnh vực

Công thức Bernoulli có nhiều ứng dụng quan trọng trong thực tiễn, từ toán học thuần túy đến các bài toán kỹ thuật. Sự đa dạng trong ứng dụng giúp công thức trở thành công cụ hữu ích cho nhiều ngành nghề khác nhau.

Ứng dụng trong toán học

Trong lĩnh vực toán học, ứng dụng công thức bernoulli thường xuất hiện trong các bài toán về xác suất và thống kê. Công thức có mối liên hệ chặt chẽ với xác suất bayes khi giải quyết các bài toán về phân phối xác suất có điều kiện.

Bài tập mẫu về công thức Bernoulli trong đại số

Giả sử cần tính xác suất để một học sinh làm đúng 3 câu trong bài kiểm tra 5 câu trắc nghiệm, biết xác suất làm đúng mỗi câu là 0.6. Ta áp dụng công thức:

P(X=3) = C(5,3) × (0.6)³ × (0.4)² = 10 × 0.216 × 0.16 = 0.3456

Ứng dụng trong vật lý và cơ học chất lỏng

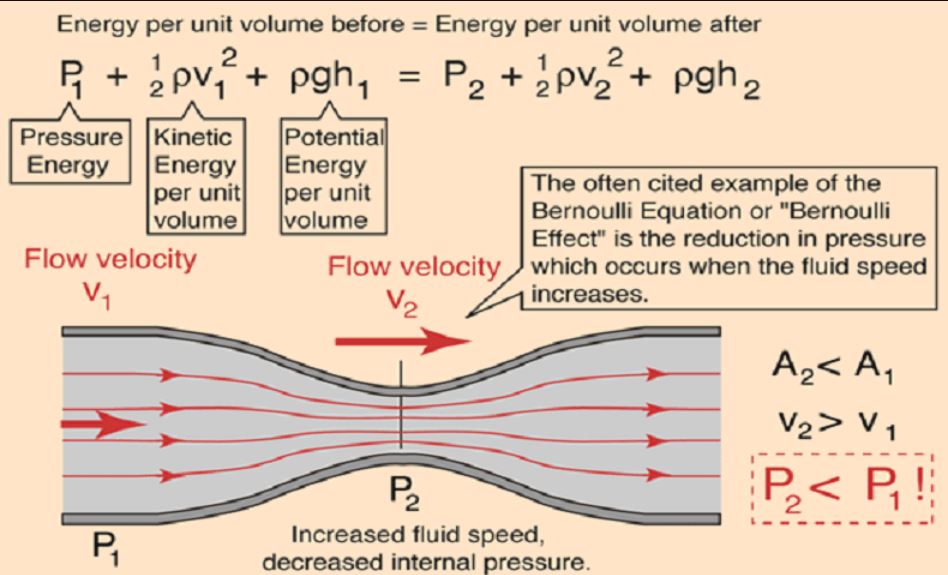
Công thức bernoulli vật lý đóng vai trò then chốt trong việc giải thích nhiều hiện tượng tự nhiên. Trong bernoulli cơ học chất lỏng, công thức mô tả mối quan hệ giữa áp suất và vận tốc của chất lỏng chảy trong ống dẫn.

Ví dụ tính toán áp suất chất lỏng

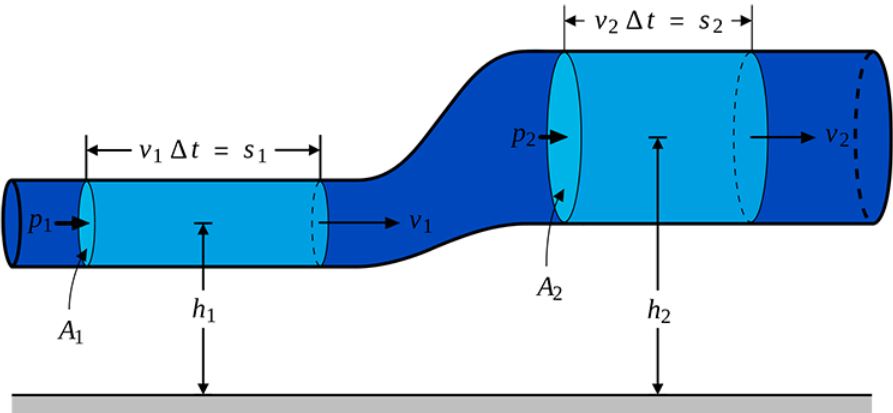
Một ống nước có tiết diện thay đổi, với đường kính đầu vào 4cm và đầu ra 2cm. Nếu vận tốc nước tại đầu vào là 2m/s, áp suất là 200kPa, ta có thể tính được áp suất tại đầu ra bằng cách áp dụng phương trình Bernoulli:
P₁ + ½ρv₁² = P₂ + ½ρv₂²
Kết quả cho thấy áp suất tại đầu ra giảm xuống còn 184kPa.

Phương pháp giải các bài toán liên quan đến công thức Bernoulli

Công thức Bernoulli là một trong những công thức quan trọng trong toán học, đặc biệt khi giải quyết các bài toán về xác suất và thống kê. Với kinh nghiệm 30 năm giảng dạy, tôi nhận thấy nhiều học sinh gặp khó khăn khi áp dụng công thức bernoulli đơn giản vào giải bài tập.

Các dạng bài tập thường gặp

Khi giảng dạy về bài tập công thức bernoulli, tôi thường phân loại thành 3 nhóm chính để học sinh dễ nắm bắt. Nhóm thứ nhất là các bài tập tính xác suất cơ bản với phép thử Bernoulli. Nhóm thứ hai là bài tập tìm số lần thử n để đạt xác suất mong muốn. Nhóm thứ ba là các bài toán ứng dụng thực tế như kiểm định chất lượng sản phẩm.

Phương pháp giải chi tiết kèm ví dụ

Trước khi đi vào giải các bài tập mẫu, cần hiểu rõ về đường sinh là gì và mối liên hệ với công thức Bernoulli. Điều quan trọng là xác định được các yếu tố cơ bản như xác suất thành công p, số lần thử n và số lần thành công k.

Bài tập mẫu 1: Tính toán cơ bản

Xem thêm : Cập nhật công thức tính mốt, trung vị chính xác nhất

Giả sử một học sinh làm bài trắc nghiệm 4 câu, mỗi câu có 4 đáp án. Em này chọn ngẫu nhiên các đáp án. Tính xác suất em đó trả lời đúng đúng 2 câu.

Giải:
– Xác suất trả lời đúng 1 câu: p = 1/4
– Số lần thử: n = 4
– Số lần thành công: k = 2
Áp dụng công thức: P(X=2) = C(4,2) × (1/4)^2 × (3/4)^2 = 0.2109375

Bài tập mẫu 2: Ứng dụng nâng cao

Một nhà máy sản xuất bóng đèn với tỷ lệ sản phẩm lỗi là 5%. Cần kiểm tra bao nhiêu bóng đèn để có thể phát hiện ít nhất 1 bóng lỗi với xác suất 95%?

Giải:
P(ít nhất 1 lỗi) = 1 – P(không có lỗi)
0.95 = 1 – 0.95^n
Giải phương trình logarit ta được n ≈ 59 bóng đèn

Mẹo và kỹ thuật ghi nhớ công thức Bernoulli hiệu quả

Việc ghi nhớ công thức bernoulli có thể trở nên dễ dàng hơn thông qua các phương pháp trực quan và thực tế. Với kinh nghiệm 30 năm giảng dạy, tôi nhận thấy học sinh thường gặp khó khăn khi phải thuộc lòng các công thức phức tạp. Tuy nhiên, bằng cách áp dụng các kỹ thuật ghi nhớ phù hợp, việc nắm vững công thức sẽ không còn là thách thức.

Phương pháp ghi nhớ theo sơ đồ

Một trong những cách nhớ công thức bernoulli hiệu quả là sử dụng sơ đồ tư duy. Bạn có thể vẽ một hình tròn ở giữa với chữ “Bernoulli”, sau đó kẻ các nhánh ra xung quanh thể hiện các thành phần của công thức. Mỗi nhánh sẽ chứa một yếu tố quan trọng như áp suất, vận tốc và độ cao. Phương pháp này giúp não bộ liên kết các thông tin theo logic tự nhiên.

Ngoài ra, việc sử dụng màu sắc khác nhau cho từng thành phần trong sơ đồ sẽ kích thích trí nhớ thị giác. Ví dụ: màu đỏ cho áp suất, màu xanh cho vận tốc và màu vàng cho độ cao. Cách tiếp cận này đặc biệt phù hợp với những học sinh có trí nhớ hình ảnh tốt.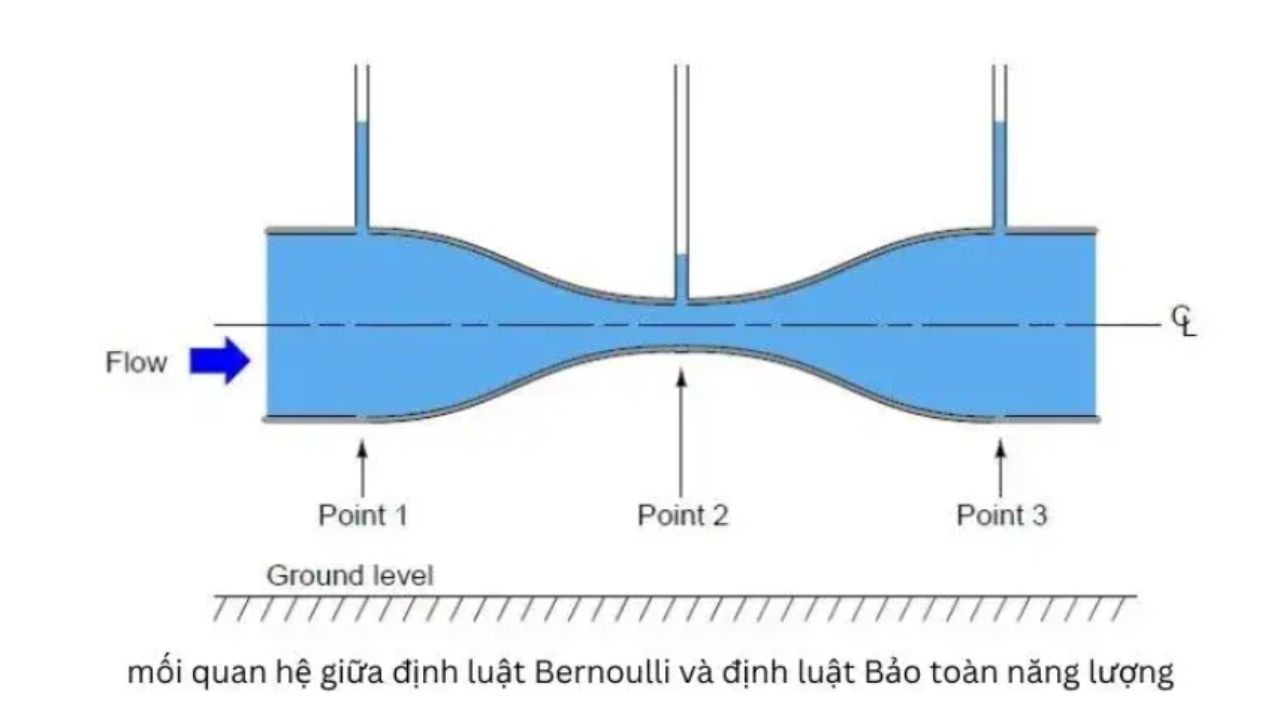

Các ví dụ thực tế giúp dễ nhớ

Liên hệ công thức với các hiện tượng trong cuộc sống sẽ giúp việc ghi nhớ trở nên tự nhiên hơn. Ví dụ như dòng nước chảy qua vòi sen – khi đường ống hẹp lại, tốc độ nước tăng lên và áp suất giảm xuống. Hoặc quan sát cánh máy bay – không khí di chuyển nhanh hơn ở phía trên cánh tạo ra áp suất thấp hơn, giúp máy bay cất cánh.

Một ví dụ thực tế khác là khi bạn uống nước bằng ống hút. Khi bạn hút, tạo ra vùng áp suất thấp trong ống, khiến chất lỏng di chuyển lên theo nguyên lý Bernoulli. Những ví dụ đơn giản như vậy sẽ giúp học sinh dễ dàng liên hệ và ghi nhớ công thức lâu hơn.

FAQ: Câu hỏi thường gặp về công thức Bernoulli

Để hiểu rõ hơn về công thức Bernoulli, tôi sẽ giải đáp một số thắc mắc phổ biến mà học sinh thường gặp phải khi học về chủ đề này.

Sự khác biệt giữa định lý và công thức Bernoulli?

Định lý Bernoulli là một nguyên lý cơ bản trong cơ học chất lỏng, mô tả mối quan hệ giữa áp suất, vận tốc và độ cao của chất lỏng chảy. Còn công thức Bernoulli là biểu thức toán học cụ thể của định lý này, giúp tính toán các đại lượng liên quan đến Bernoulli áp suất chất lỏng.

Mối liên hệ giữa phương trình và công thức Bernoulli?

Phương trình Bernoulli là dạng phương trình vi phân bậc nhất đặc biệt, có dạng y’ + P(x)y = Q(x)y^n. Công thức Bernoulli được sử dụng để giải phương trình này thông qua phép biến đổi đổi biến. Mối liên hệ giữa chúng thể hiện tính ứng dụng của Bernoulli toán học trong việc giải quyết các bài toán thực tế.

Tại sao công thức Bernoulli quan trọng trong chương trình toán 12?

Bernoulli toán 12 là một phần quan trọng giúp học sinh hiểu được ứng dụng của toán học trong thực tế, đặc biệt trong lĩnh vực vật lý và kỹ thuật. Công thức này không chỉ giúp giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng để học sinh tiếp cận với các bài toán phức tạp hơn ở bậc đại học.

Việc nắm vững **công thức Bernoulli** giúp học sinh giải quyết nhiều bài toán trong chương trình phổ thông và đại học. Công thức này không chỉ là nền tảng quan trọng trong toán học mà còn có ứng dụng thiết thực trong vật lý và cơ học chất lỏng. Với cách tiếp cận từ cơ bản đến nâng cao kèm các ví dụ minh họa cụ thể, các em có thể tự tin áp dụng công thức này vào giải quyết nhiều dạng bài tập khác nhau.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê