Công thức tính diện tích hình hộp chữ nhật – Lý thuyết và vận dụng

Công thức tính diện tích hình hộp chữ nhật được giải thích đơn giản, dễ hiểu kèm theo bài tập cụ thể. Lưu lại và ghi nhớ chính xác để áp dụng linh hoạt trong các bài toán và đời sống.

Công thức tính diện tích hình hộp chữ nhật

Diện tích hình hộp chữ nhật bao gồm diện tích xung quanh và diện tích toàn phần.

Bạn đang xem: Công thức tính diện tích hình hộp chữ nhật – Lý thuyết và vận dụng

1/ Công thức tính diện tích xung quanh hình hộp chữ nhật

Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật. Diện tích hai mặt đáy không được tính đến.

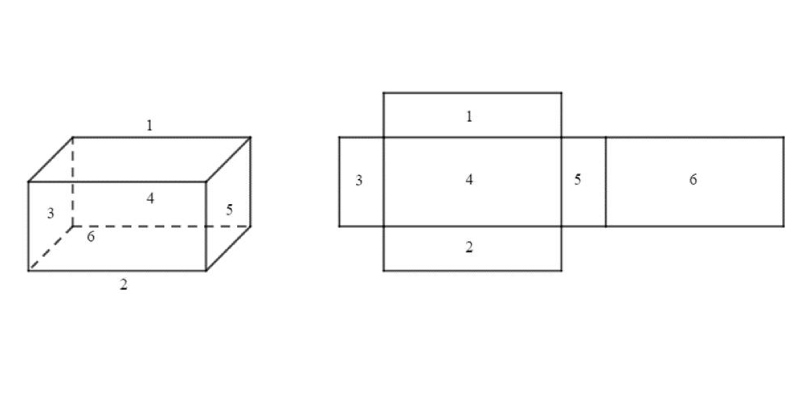
Công thức tính diện tích xung quanh của hình hộp chữ nhật như sau:

Sxq = (a + b) × 2 × h = Chu vi mặt đáy x h

Trong đó:

• Sxq là diện tích xung quanh của hình hộp chữ nhật
• a là chiều dài của hình hộp chữ nhật
• b là chiều rộng của hình hộp chữ nhật
• h là chiều cao của hình hộp chữ nhật

2/ Công thức tính diện tích toàn phần hình hộp chữ nhật

Diện tích toàn phần của hình hộp chữ nhật là tổng diện tích tất cả các mặt của hình hộp chữ nhật. Diện tích này bao gồm cả diện tích xung quanh và diện tích hai mặt đáy.

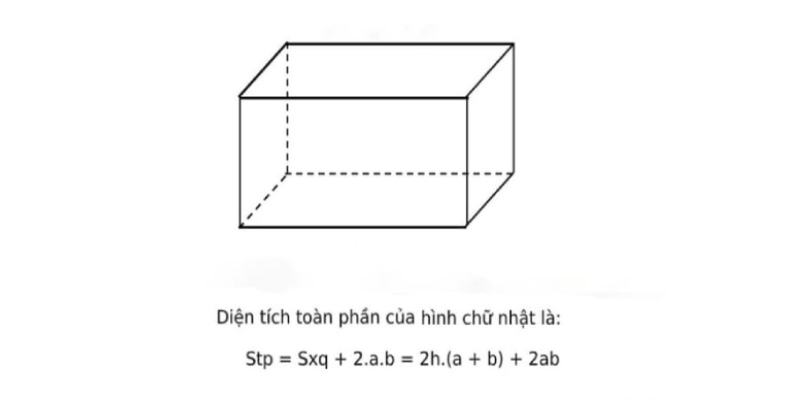
Công thức tính diện tích toàn phần của hình hộp chữ nhật như sau:

Stp = Sxq + Sđáy × 2 = (a + b) x 2 x h + 2 x a x b

Trong đó:

• Stp là diện tích toàn phần của hình hộp chữ nhật
• Sxq là diện tích xung quanh của hình hộp chữ nhật
• Sđáy là diện tích 01 mặt đáy của hình hộp chữ nhật
• a là chiều dài của hình hộp chữ nhật
• b là chiều rộng của hình hộp chữ nhật
• h là chiều cao của hình hộp chữ nhật

Bài tập vận dụng công thức diện tích xung quanh, toàn phần

Áp dụng chính xác và linh hoạt các công thức tính diện tích bằng cách tập giải các bài tập dưới đây. Tự giải và kiểm tra lại đáp án để kiểm tra năng lực của bản thân.

Bài tập 1: Áp dụng công thức tính diện tích xung quanh

Tính diện tích xung quanh của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 7cm và chiều cao 5cm.

Xem thêm : Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải

Bài giải:

Diện tích xung quanh của hình hộp chữ nhật là:

Sxq = (a + b) × 2 × h

=> Sxq = (8 + 7) x 2 x 5 = 150 cm2

Bài tập 2: Áp dụng công thức tính diện tích toàn phần

Tính diện tích toàn phần của một hình chữ nhật có chiều cao là 3cm, chiều dài là 5,4cm, chiều rộng là 2cm.

Xem thêm : Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải

Bài giải:

Diện tích xung quanh của hình chữ nhật là:

Sxq = 2h(a + b)

Xem thêm : Khám phá công thức tính thể tích khối tứ diện và các phương pháp giải hay nhất

=> Sxq = 2 x 3 x (5,4 +2) = 44,4 cm2

Diện tích mặt đáy của hình chữ nhật là:

Sđáy = 5,4 x 2 = 10,8 cm2

Diện tích toàn phần của hình chữ nhật là:

Stp = Sxq + Sđáy

=> Stp = 44,4 + 2 x 10.8 = 66  cm2

Bài tập 3: Xác định chiều cao dựa trên diện tích cho trước

Tính chiều cao của hình hộp chữ nhật, biết diện tích xung quanh của hình hộp là 217,5m2 và nửa chu vi mặt đáy bằng 14,5m.

Bài giải

Chu vi mặt đáy của hình hộp chữ nhật đó là:

14,5 × 2 = 29 (m)

Chiều cao của hình hộp chữ nhật đó là:

h = Sxq : chu vi mặt đất

=> h = 217,5 : 29 = 7,5 (m)

Bài tập 4: Xác định chu vi hình hộp chữ nhật dựa trên diện tích xung cho trước

Một hình hộp chữ nhật có diện tích xung quanh là 420 cm2 và có chiều cao là 7cm. Tính chu vi đáy của hình hộp chữ nhật đó.

Xem thêm : Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải

Bài giải:

Ta có: Sxq = (a + b) × 2 × h = Chu vi mặt đáy x h

=> Chu vi mặt đáy = Sxq/h

=> Chu vi mặt đáy = 420 : 7 = 60 (cm)

Vậy, chu vi mặt đáy của hình hộp chữ nhật là 60 cm.

Bài  tập 5: Xác định chênh lệch diện tích toàn

Một cái hộp dạng hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 15 cm và chiều cao 10cm. An dán giấy màu tím vào các mặt xung quanh và dán giấy màu xanh vào hai mặt đáy của hộp đó (chỉ dán mặt ngoài). Hỏi diện tích giấy màu nào lớn hơn và lớn hơn bao nhiêu xăng – ti -mét vuông?

Xem thêm : Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải

Bài giải:

Diện tích giấy màu tím là diện tích xung quanh của hình hộp chữ nhật:

Sxq = (a + b) × 2 × h

=> Sxq = ( 20 + 15) x 2 x 10 = 700 cm2

Diện tích giấy màu xanh là diện tích mặt đáy của hình hộp chữ nhật là:

Sđáy = 2 x a x b=

=> Sđáy =  (20 x 15) x 2 = 600 cm2

Diện tích giấy màu tím lớn hơn diện tích giấy màu xanh là: 700 – 600 = 100 cm2

Bài tập 6: Bài tập vận dụng tính diện tích thực tế

Hoa muốn quét vôi các bức tường xung quanh và trần của căn phòng dạng hình hộp chữ nhật có chiều dài 6m, chiều rộng 48dm, chiều cao 4m. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng 12m2 (biết rằng chỉ quét vôi bên trong phòng)?

Bài giải

48dm = 4,8m

Diện tích xung quanh của căn phòng đó là:

Sxq = (a + b) × 2 × h

=> Sxq= (6 + 4,8) × 2 × 4 = 86,4 (m2)

Diện tích trần của căn phòng (diện tích một mặt đáy) đó là:

S1đáy = 6 × 4,8 = 28,8 (m2)

Diện tích cần quét vôi không bao gồm diện tích cửa và diện tích nền nhà. Ta có:

S quét vôi = Sxq + S1đáy – Scửa

=> S quét vôi = 86,4 + 28,8 – 12 = 103,2 (m2)

Vậy tổng diện tích Hoa cần quét vôi là 103,2m2

Kết luận

Ghi nhớ công thức tính diện tích hình hộp chữ nhật dễ dàng thông qua bài tập vận dụng và lời giải chi tiết. Hy vọng kiến thức hữu ích trên sẽ giúp bạn đạt được kết quả cao trong kỳ thi sắp tới.

Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian