Cập nhật công thức tính mốt, trung vị chính xác nhất

Công thức tính mốt, trung vị được sử dụng cực kỳ phổ biến trong lĩnh vực xác suất thống kê. Bạn cần lưu ý nắm bắt chuẩn xác khái niệm để làm bài tập, tránh nhầm lẫn với trung bình.

Khái niệm mốt và trung vị là như thế nào?

Chắc hẳn bạn đã quá quen với thuật ngữ trung bình cộng là gì trong tính toán. Tuy nhiên, đôi khi công thức này không thể hỗ trợ chuẩn các bài toán quá dài với những tổ hợp dữ liệu phức tạp.

Bạn đang xem: Cập nhật công thức tính mốt, trung vị chính xác nhất

Vì vậy, khái niệm trung vị cùng mốt được ra đời để phục vụ lĩnh vực xác suất thống kê.

Mốt

Mốt là giá trị Xi có tần số Ni lớn nhất trong bảng phân số tần số, nếu có từ hai giá trị bằng nhau thì nói là có hai mốt. Ký hiệu của mốt là Mo, nếu có hai mốt thì là Mo1,Mo2.

Trung vị

Khái niệm trung vị chỉ giá trị nằm ở trung tâm của một dãy số (thường dưới dạng tập hợp) với điều kiện dãy này phải được sắp xếp từ thấp đến cao.

Trung vị ra đời nhằm thực hiện vai trò tốt hơn cho số trung bình khi các số liệu trong mẫu có sự chênh lệch quá lớn với nhau. Nó nằm ở giữa của dãy số, nghĩa là khoảng cách với các số xung quanh bằng nhau.

Ví dụ trong dãy số 1,3,5,7,9,11,23,27,49 thì 9 là trung vị, bên phải số 9 có bốn số và bên trái có bốn số.

Đặc điểm:

• Chỉ được xác định khi nằm trong dãy số sắp xếp theo thứ tự từ nhỏ đến lớn.
• Trung vị của dãy số chẵn và lẻ khác nhau với công thức tính khác nhau. Thường với dãy chẵn sẽ tính dựa trên công thức cụ thể là trung bình cặp số ở giữa, còn dãy lẻ thì lấy số nằm chính giữa dãy. Công thức tính trung vị cụ thể sẽ được cập nhật ở phần tiếp theo để bạn nhận biết.
• Trung vị khác trung bình, trong dãy chứa trung vị phải có điểm ngoại lai nghĩa là cách giá trị cách nhau không đều, đôi khi là chênh lệch quá lớn.

Công thức tính mốt và trung vị cụ thể

Tính mốt không có công thức cụ thể mà dựa vào tần số được cho trong bảng số liệu. Giá trị nào có tần số cao nhất thì được xác định là mốt và khi viết thì viết là Mo = Giá trị.

Xem thêm : Hướng dẫn công thức tổ hợp và chỉnh hợp cho học sinh trung học phổ thông

Công thức trung vị thì phức tạp hơn một chút tùy vào dãy số liệu là chẵn hay lẻ. Dạng chung được xác định là: Me = [(n+1)/2] với n là số dữ liệu ở trong tập hợp đó.

Trường hợp dãy là số lẻ thì vị trí của trung vị là ở giữa dãy với công thức tính là:

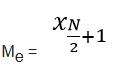
Nếu dãy là số chẵn thì công thức tính trung vị bằng trung bình của cặp số đứng giữa (trung bình cộng hai số):

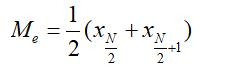
Ứng dụng của trung vị và mốt trong thực tế

Công thức tính mốt, trung vị không chỉ giúp học sinh giải bài tập trên lớp mà còn có giá trị trong cuộc sống. Bạn có thể bắt gặp một số trường hợp có ứng dụng những khái niệm này như:

• Quản trị kinh doanh: Công thức có tác dụng điều chỉnh chi phí sản phẩm sao cho đáp ứng được nhu cầu của các phân khúc khách hàng. Nhất là khi các sản phẩm của công ty có sự chênh lệch lớn, nếu tính trung bình ra thì cách quá xa mức thấp nhất và cao nhất.
• Phân nhóm dữ liệu: Thay vì tính trung bình thì tính trung vị sẽ ra được một mức phù hợp hơn để phân chia. Không chỉ với các con số mà đôi khi còn là hàng hoá, con người, dịch vụ,… Chẳng hạn khi cần chia một lớp học thành các nhóm, bạn có thể dựa vào trung vị chiều cao.
• Mức lương ở các doanh nghiệp: Nếu so sánh thì lương trung vị sẽ tạo ra cái nhìn tổng quát, rộng mở hơn so với lương trung bình. Trong kinh doanh, khái niệm này được gọi là thu nhập 50% nghĩa là một nửa làm việc với lương cao hơn, một nửa thấp hơn tạo ra cạnh tranh lành mạnh. Nhiều công ty cung cấp số liệu này để kích thích sự nỗ lực phát triển ở nhân viên.

Phân biệt trung vị và trung bình chính xác nhất

Cảm giác và thực tế thì số trung vị mang đến cái nhìn mở rộng hơn cho các số liệu. Trong một danh sách, lấy số ở giữa là cách để mô tả rõ ràng về tập hợp số liệu hơn là trung bình.

Trung vị cũng không bị ảnh hưởng bởi các yếu tố ngoại lai nhiều như trung bình. Bởi đôi khi giá trị đơn lẻ nào đó quá thấp hay quá cao sẽ khiến số trung bình khác đi, không phản ánh rõ đặc điểm của dãy dữ liệu.

Bài tập về công thức mốt và trung vị cùng lời giải

Mỗi một ví dụ đều có cách làm cụ thể giúp bạn hiểu về khái niệm mốt, trung vị là như thế nào cũng với cách ứng dụng trong bài tập toán.

Bài tập với mốt

Để hiểu hơn về công thức tính mốt thì bạn có thể tham khảo ví dụ được Congthuctoan chia sẻ sau đây.

Ví dụ tìm trung vị của tập hợp số lẻ

Xem thêm : Chi tiết công thức tính trung bình cộng và hướng dẫn các bài tập ứng dụng cơ bản

Đề bài: Cho dãy số gồm 23,51,63,77,27,29,40 và tìm trung vị.

Cách giải: Đầu tiên phải xếp các số thành một dãy có giá trị từ thấp đến cao như sau: 23,27,29,40,51,63,77.

Dãy gồm có bảy số, số ở giữa là 40 (bên phải ba số và bên trái ba số) nên 40 là trung vị. Trường hợp trong dãy là các số thập phân thì việc xác định cũng tương tự, bạn đừng quá chú ý đến đơn vị sau dấu phẩy.

Ví dụ xác định trung vị của tập hợp gồm các số chẵn

Đề bài: Tìm trung vị của dãy số gồm 103, 55, 31, 97, 85, 100, 11, 51.

Cách giải: Bước đầu tiên là bạn cần sắp xếp dãy số thành một dãy từ bé đến lớn cụ thể: 11,31,51,55,85,97,100,103. Từ đó thấy được đây là dãy chẵn nên không thể xác định số ở giữa là trung vị.

Vậy để tính được thì phải áp dụng công thức là tính trung bình cộng của hai số nằm giữa, đó là 55 và 86. Tính được (55+85)/2 = 70 vậy nên trung vị là 70.

Lưu ý khi thực hành với số liệu thống kê

Công thức tính mốt, trung vị mang đến thêm các lựa chọn mới khi tìm đại diện cho một bảng số liệu.

Chọn đại diện cho các số liệu thống kê có thể là trung bình cộng khi tập hợp không có nhiều điểm ngoại lai. Còn nếu có thì nên chọn trung vị cho chính xác.

Trung bình cũng nên được dùng cho số lượng thống kê lớn với n từ 30 trở lên. Nếu n chỉ bé hơn hoặc bằng 10 thì trung vị là tối ưu nhất, bên cạnh đó xác định thêm mốt.

Kết luận

Công thức tính mốt, trung vị có ý nghĩa to lớn với quá trình học xác suất thống kê. Bạn hãy nắm vững công thức được áp dụng cho các trường hợp cụ thể để đưa ra lời giải chính xác cho các bài toán.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê