Công thức tính diện tích hình trụ và bài tập ứng dụng có đáp án

Thầy giáo toán với hơn 30 năm kinh nghiệm giảng dạy hướng dẫn chi tiết **công thức tính diện tích hình trụ** qua các ví dụ thực tế. Bài viết trình bày đơn giản, dễ hiểu các phương pháp tính diện tích đáy, diện tích xung quanh và diện tích toàn phần của hình trụ kèm bài tập mẫu phù hợp với mọi trình độ học sinh.

Các thành phần cơ bản và cách tính diện tích hình trụ

Hình trụ là một khối hình học 3 chiều phổ biến, được ứng dụng rộng rãi trong thực tế. Việc nắm vững cách tính diện tích hình trụ sẽ giúp giải quyết nhiều bài toán thực tiễn.

Bạn đang xem: Công thức tính diện tích hình trụ và bài tập ứng dụng có đáp án

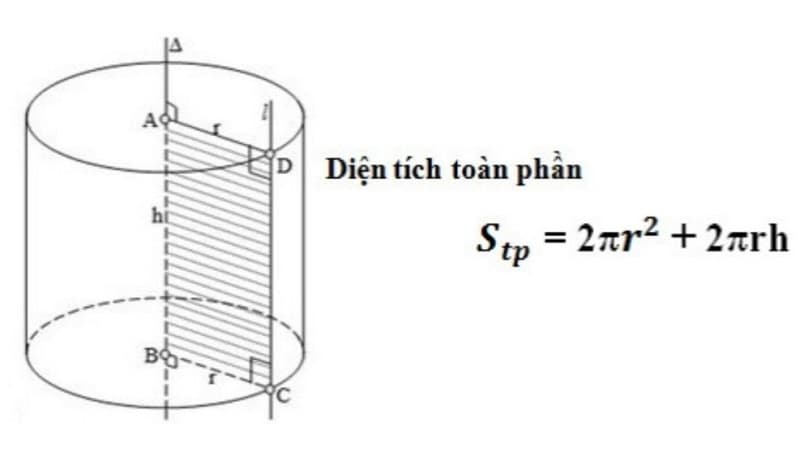
Khái niệm và đặc điểm của hình trụ tròn xoay

Công thức hình trụ tròn xoay được xây dựng dựa trên đặc điểm cấu tạo của nó. Hình trụ tròn xoay là hình khối tạo bởi một hình tròn quay quanh một trục vuông góc với mặt phẳng chứa hình tròn đó. Hình trụ có hai đáy là hai hình tròn bằng nhau và song song với nhau.

Các yếu tố cần xác định khi tính diện tích hình trụ

Để tính diện tích hình trụ, cần xác định chính xác các thành phần: bán kính đáy (r), chiều cao hình trụ (h), và số π (≈ 3,14). Các yếu tố này quyết định độ chính xác của kết quả tính toán. Bạn có thể sử dụng công cụ tính diện tích hình tròn online để kiểm tra kết quả.

Công thức tính diện tích đáy hình trụ với ví dụ minh họa

Tính diện tích đáy hình trụ áp dụng công thức

S = πr²

Trong đó r là bán kính đáy.

Diện tích này giống nhau ở cả hai đáy do tính chất đối xứng của hình trụ tròn xoay. Ví dụ, với bán kính đáy 5cm, diện tích đáy sẽ là: S = 3,14 × 5² = 78,5 cm².

Xem thêm : Khám phá công thức tính diện tích xung quanh hình trụ và bài tập ứng dụng

Bài tập mẫu tính diện tích đáy hình trụ

Cho hình trụ có bán kính đáy 3cm. Tính diện tích đáy của hình trụ.
Giải:
– Áp dụng công thức S = πr²
– Thay số: S = 3,14 × 3² = 3,14 × 9 = 28,26 cm²
Vậy diện tích đáy hình trụ là 28,26 cm².

Hướng dẫn chi tiết cách tính diện tích xung quanh và toàn phần hình trụ

Để tính chính xác diện tích của một hình trụ, chúng ta cần nắm vững hai thành phần quan trọng: diện tích xung quanh và diện tích toàn phần. Mỗi thành phần có công thức riêng và cách áp dụng khác nhau tùy theo bài toán cụ thể.

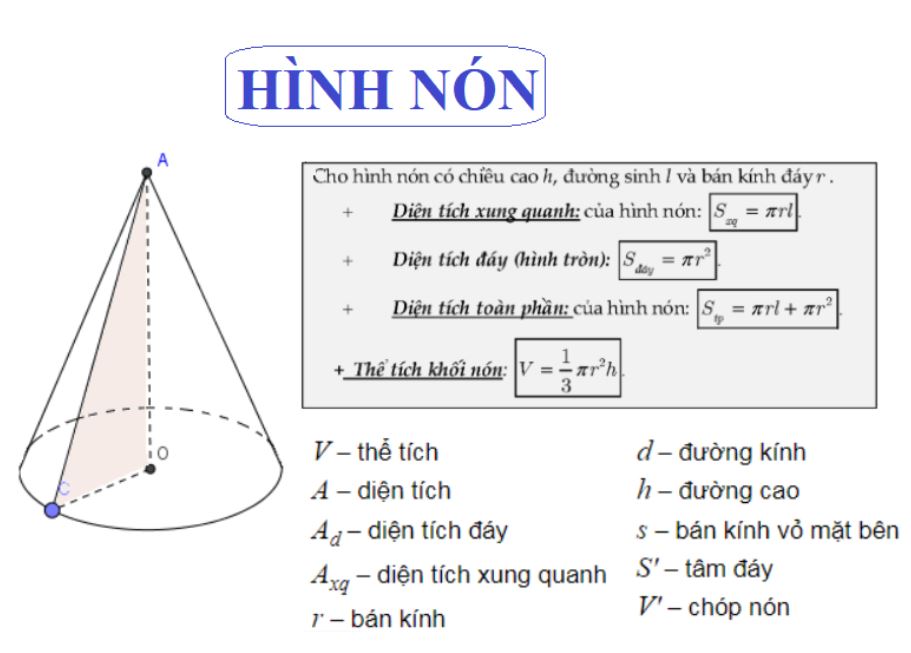
Công thức tính diện tích xung quanh hình trụ

Công thức tính diện tích xung quanh hình trụ được xác định bằng tích của chu vi đáy và chiều cao hình trụ. Cụ thể:

Sxq = 2πrh

Trong đó r là bán kính đáy, h là chiều cao

Công thức tính diện tích xung quanh hình trụ giúp ta hình dung rõ hơn về mặt xung quanh của hình trụ khi trải phẳng sẽ tạo thành một hình chữ nhật.

Ví dụ tính diện tích xung quanh hình trụ đứng

Một hình trụ có bán kính đáy r = 5cm và chiều cao h = 10cm.
Áp dụng công thức: Sxq = 2πrh = 2 × 3,14 × 5 × 10 = 314 (cm²)

Công thức tính diện tích toàn phần của hình trụ

Diện tích toàn phần hình trụ bằng tổng của diện tích xung quanh và diện tích hai đáy. Công thức:

Xem thêm : Khám phá công thức diện tích hình cầu và bài tập mẫu có lời giải

Stp = 2πrh + 2πr² = 2πr(h + r)

Việc tính toán cần chú ý đơn vị đo phải thống nhất để tránh sai sót.

Bài tập mẫu tính diện tích toàn phần hình trụ có đáy

Cho hình trụ có bán kính đáy r = 3cm và chiều cao h = 8cm.
Diện tích toàn phần: Stp = 2πr(h + r) = 2 × 3,14 × 3(8 + 3) = 207,24 (cm²)

Error: No text generated.

FAQ: Câu hỏi thường gặp về tính diện tích hình trụ

Việc tính toán diện tích hình trụ thường gây nhiều khó khăn cho học sinh. Sau đây là một số câu hỏi phổ biến giúp các em nắm vững kiến thức này tốt hơn.

Làm thế nào để phân biệt diện tích xung quanh và toàn phần?

Diện tích xung quanh chỉ tính phần diện tích mặt cong của hình trụ, còn diện tích toàn phần bao gồm cả hai đáy và mặt cong. Giống như khi bạn mua một lon nước ngọt, diện tích xung quanh là phần nhãn dán bên ngoài, còn diện tích toàn phần tính cả đáy trên và đáy dưới của lon. Cách tính diện tích hình trụ cần phân biệt rõ hai khái niệm này để tránh nhầm lẫn khi giải toán.

Tại sao cần học cách tính diện tích hình trụ?

Kiến thức về cách tính diện tích trụ tròn rất thiết thực trong cuộc sống. Ví dụ khi tính lượng sơn cần mua để sơn cột nhà, tính diện tích giấy gói quà hình trụ, hay thiết kế bao bì sản phẩm. Ngoài ra, kiến thức này còn liên quan đến công thức tính diện tích mặt cầu ngoại tiếp và nhiều hình học không gian khác.

Những sai lầm thường gặp khi tính diện tích hình trụ

Sai lầm phổ biến nhất là nhầm lẫn giữa diện tích xung quanh và toàn phần. Nhiều học sinh quên không nhân 2 khi tính diện tích hai đáy. Một số em cũng nhầm lẫn giữa bán kính và đường kính khi áp dụng công thức, dẫn đến kết quả sai lệch gấp đôi. Việc làm tròn số π cũng cần chú ý để đảm bảo độ chính xác của kết quả.

Các phương pháp tính toán và **công thức tính diện tích hình trụ** đã được trình bày chi tiết từ cơ bản đến nâng cao. Việc nắm vững các công thức tính diện tích đáy, diện tích xung quanh và diện tích toàn phần giúp học sinh giải quyết tốt các bài toán hình học không gian. Thông qua các ví dụ minh họa và bài tập mẫu, các em có thể áp dụng linh hoạt kiến thức vào thực tế và phát triển tư duy không gian.

Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian