Khám phá công thức diện tích hình cầu và bài tập mẫu có lời giải
Bài toán về **công thức tính diện tích hình cầu** luôn là một chủ đề quan trọng trong chương trình hình học không gian. Với phương pháp giảng dạy đơn giản hóa và các ví dụ minh họa cụ thể, chúng ta có thể dễ dàng nắm bắt cách áp dụng công thức này vào các bài toán từ cơ bản đến nâng cao trong chương trình phổ thông.
- Hướng dẫn công thức tính khoảng cách giữa hai đường thẳng và bài tập mẫu có lời giải
- Hướng dẫn công thức tính thể tích hình trụ và bài tập ứng dụng có lời giải
- Công thức tính thể tích hình hộp chữ nhật – Ôn tập và giải đề chuẩn xác
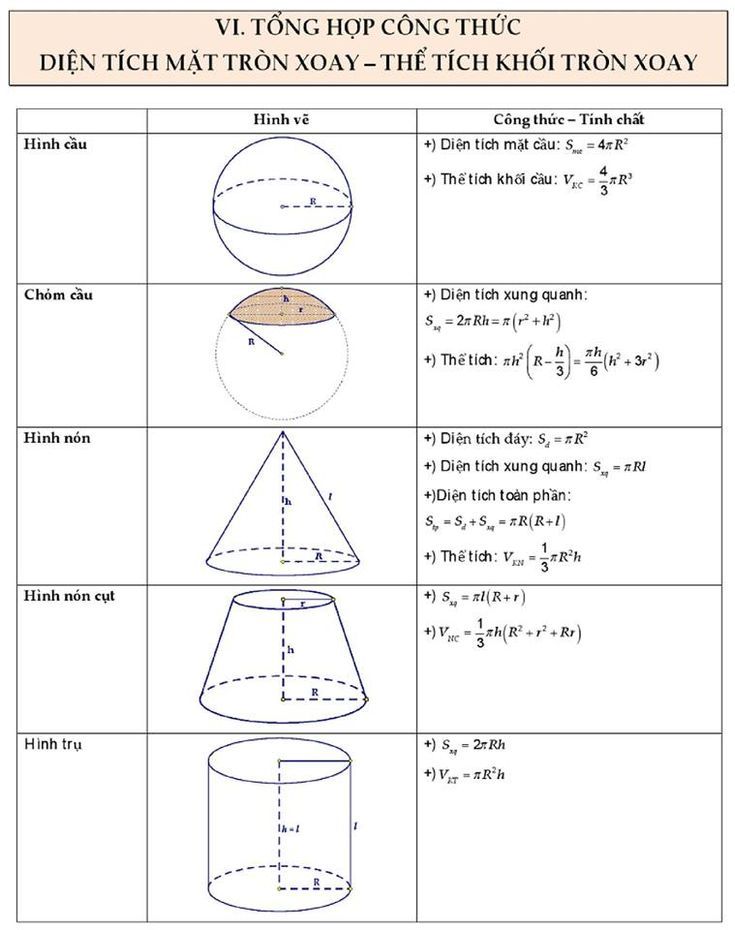
- Lý thuyết công thức thể tích khối tròn xoay và phương pháp giải chi tiết cho học sinh
- Tìm hiểu công thức tính diện tích mặt cầu và bài tập ví dụ chi tiết
Diện tích hình cầu là gì? Tìm hiểu khái niệm cơ bản về hình cầu trong không gian
Khi nói đến diện tích hình cầu trong không gian, chúng ta đang đề cập đến diện tích bề mặt của một khối cầu – một hình khối ba chiều hoàn hảo, có tất cả các điểm trên bề mặt cách đều tâm một khoảng bằng bán kính.
Diện tích hình cầu là gì? Đó chính là tổng diện tích bề mặt của khối cầu, được tính bằng công thức
S = 4πR²
Trong đó R là bán kính của hình cầu. Công thức này được nhà toán học vĩ đại Archimedes chứng minh từ thế kỷ thứ 3 trước Công nguyên.
Để dễ hình dung, tôi thường ví von với học sinh rằng diện tích hình cầu giống như diện tích vỏ quả cam – phần bề mặt bọc bên ngoài quả cam. Nếu bạn gọt vỏ cam và trải phẳng ra, diện tích phần vỏ cam đó chính là diện tích hình cầu.
Ví dụ thực tế: Một quả bóng đá FIFA tiêu chuẩn có bán kính 11cm. Áp dụng công thức trên:
S = 4 × 3,14 × 11² = 1.519,76 cm²
Đây chính là diện tích bề mặt của quả bóng mà các cầu thủ sẽ tiếp xúc khi thi đấu.
Việc hiểu rõ về diện tích hình cầu rất quan trọng trong nhiều ứng dụng thực tế, từ thiết kế kiến trúc mái vòm, sản xuất bóng thể thao, cho đến tính toán diện tích bề mặt các hành tinh trong vũ trụ.
Công thức tính diện tích hình cầu và các trường hợp áp dụng phổ biến
Khi tìm hiểu về công thức tính diện tích hình cầu, chúng ta sẽ thấy đây là một công thức khá đơn giản nhưng lại rất quan trọng trong hình học không gian. công thức tính diện tích mặt cầu giúp chúng ta giải quyết nhiều bài toán thực tế, từ tính toán diện tích bề mặt của các vật thể hình cầu đến ứng dụng trong kiến trúc và thiết kế.
Công thức tính diện tích hình cầu cơ bản theo bán kính R
Diện tích hình cầu có bán kính r được tính theo công thức:
S = 4πR²
Trong đó R là bán kính của hình cầu.
Công thức này xuất phát từ việc tính tổng diện tích của vô số các mặt phẳng nhỏ tạo nên bề mặt hình cầu. Với π ≈ 3,14, ta có thể dễ dàng áp dụng công thức vào các bài toán cụ thể.
Công thức tính diện tích hình cầu theo đường kính D
Diện tích hình cầu theo đường kính được biểu diễn qua công thức:
S = πD²
Trong đó D là đường kính của hình cầu.
Công thức này được sử dụng khi đề bài cho biết đường kính thay vì bán kính. Vì D = 2R nên khi thay vào công thức ban đầu, ta được kết quả như trên.

Bài tập mẫu về tính diện tích hình cầu đơn giản
Ví dụ: Một quả bóng có bán kính 5cm, tính diện tích bề mặt của quả bóng.
Giải:
– Áp dụng công thức S = 4πR²
– Thay số: S = 4 × 3,14 × 5² = 4 × 3,14 × 25 = 314 (cm²)
Vậy diện tích bề mặt quả bóng là 314 cm². Qua ví dụ đơn giản này, ta thấy việc áp dụng công thức tính diện tích hình cầu không quá phức tạp, chỉ cần nắm chắc công thức và thực hiện tính toán cẩn thận.
Hướng dẫn chi tiết cách tính diện tích hình cầu trong các bài toán phức tạp
Cách tính diện tích mặt cầu trong các bài toán phức tạp đòi hỏi sự hiểu biết sâu sắc về mối quan hệ giữa các yếu tố hình học. Công thức cơ bản S = 4πR² sẽ được áp dụng linh hoạt khi hình cầu nằm trong các khối hình học khác.
Diện tích hình cầu nội tiếp và ngoại tiếp trong hình lập phương
Khi xét diện tích hình cầu trong hình lập phương, ta cần phân biệt 2 trường hợp: nội tiếp và ngoại tiếp. Với hình cầu nội tiếp, đường kính hình cầu bằng cạnh hình lập phương. Với hình cầu ngoại tiếp, đường kính hình cầu bằng đường chéo hình lập phương.
Diện tích hình cầu trong hình trụ tròn xoay
Diện tích hình cầu nội tiếp trong hình trụ có mối liên hệ chặt chẽ với diện tích xung quanh hình trụ. Đường kính hình cầu bằng đường kính đáy hình trụ và chiều cao hình trụ phải bằng đường kính hình cầu để hình cầu tiếp xúc với hai đáy.
Bài tập mẫu có lời giải chi tiết
Bài toán: Cho hình lập phương cạnh a = 6cm. Tính diện tích hình cầu nội tiếp.
Lời giải:
– Đường kính hình cầu D = a = 6cm
– Bán kính hình cầu R = D/2 = 3cm
– Diện tích hình cầu S = 4πR² = 4π×3² = 36π (cm²)
Bài toán giúp minh họa cách vận dụng công thức cơ bản vào tình huống cụ thể. Khi giải các bài toán tương tự, việc xác định chính xác bán kính hình cầu là yếu tố then chốt.
Phương pháp giải các dạng bài tập về diện tích hình cầu trong chương trình phổ thông
Diện tích hình cầu là một trong những kiến thức quan trọng trong chương trình toán phổ thông. Để giải tốt các bài toán về diện tích hình cầu lớp 9 và diện tích hình cầu lớp 12, học sinh cần nắm vững công thức S = 4πR² (với R là bán kính hình cầu). Tương tự như cách tính diện tích hình vuông có đường chéo, việc áp dụng công thức cần linh hoạt theo từng dạng bài.

Các dạng bài tập điển hình về diện tích hình cầu lớp 9
Ở cấp độ lớp 9, các bài tập thường yêu cầu tính diện tích hình cầu khi biết bán kính hoặc đường kính. Một số bài tập có thể kết hợp với công thức khối cầu để tìm mối liên hệ giữa diện tích và thể tích. Học sinh cần chú ý đơn vị đo và quy đổi đơn vị phù hợp trước khi áp dụng công thức.
Các dạng bài tập nâng cao về diện tích hình cầu lớp 12
Ở chương trình diện tích hình cầu hình học 12, bài tập thường phức tạp hơn với việc kết hợp nhiều yếu tố như tam giác, hình chóp, đa diện. Các bài toán có thể yêu cầu tìm diện tích hình cầu nội tiếp hoặc ngoại tiếp các hình khối khác, đòi hỏi học sinh phải vận dụng kiến thức hình học không gian một cách tổng hợp.
Phân tích lời giải chi tiết các bài tập khó
Khi giải các bài tập khó về diện tích hình cầu, học sinh cần tuân theo quy trình: Vẽ hình minh họa chính xác, xác định các yếu tố đã cho và cần tìm, thiết lập mối quan hệ giữa các yếu tố thông qua các định lý hình học không gian, cuối cùng là áp dụng công thức tính diện tích hình cầu. Việc kiểm tra kết quả bằng cách ước lượng sơ bộ sẽ giúp tránh những sai sót không đáng có.
FAQ: Câu hỏi thường gặp về diện tích hình cầu
Khi học về hình cầu, nhiều học sinh thường gặp khó khăn trong việc tính toán diện tích. Tôi sẽ giải đáp một số thắc mắc phổ biến để giúp các em nắm vững kiến thức này.
Diện tích mặt cầu bằng bao nhiêu khi biết bán kính?
Diện tích mặt cầu bằng 4πR², trong đó R là bán kính hình cầu. Ví dụ với hình cầu có bán kính 5cm, diện tích sẽ là 4π×5² = 314,16 cm². Công thức này rất dễ nhớ vì nó chỉ cần bình phương bán kính rồi nhân với 4π.
Làm thế nào để tính diện tích hình cầu ngoại tiếp một hình khối?
Để tính công thức tính diện tích mặt cầu ngoại tiếp, trước tiên cần xác định bán kính hình cầu. Bán kính hình cầu ngoại tiếp sẽ bằng đường cao của hình chóp từ tâm đến mặt đáy. Sau khi có bán kính, áp dụng công thức 4πR² để tính diện tích.
Có những phương pháp nào để tính diện tích hình cầu đơn giản nhất?
Tính diện tích hình cầu đơn giản nhất là sử dụng máy tính bỏ túi với công thức 4πR². Ngoài ra, có thể ước lượng nhanh bằng cách nhân bán kính bình phương với 12,56. Phương pháp này cho kết quả gần đúng và tiện lợi khi làm bài tập nhanh hoặc kiểm tra đáp án.
Việc áp dụng **công thức tính diện tích hình cầu** đòi hỏi sự hiểu biết chính xác về các yếu tố hình học trong không gian. Các công thức cơ bản theo bán kính và đường kính giúp giải quyết nhiều bài toán đơn giản. Đối với các trường hợp phức tạp như hình cầu nội tiếp, ngoại tiếp trong hình lập phương hay hình trụ, học sinh cần nắm vững mối liên hệ giữa các yếu tố hình học. Kiến thức này tạo nền tảng quan trọng cho việc học tập toán học không gian ở các cấp độ cao hơn.
Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian
Bài viết liên quan

Hướng dẫn công thức tính khoảng cách giữa hai đường thẳng và bài tập mẫu có lời giải
Tìm hiểu chi tiết công thức tính khoảng cách giữa hai đường thẳng với các trường hợp song song, chéo nhau, cắt nhau trong không gian và mặt phẳng. Kèm bài tập mẫu có lời giải.

Khám phá công thức tính diện tích xung quanh hình trụ và bài tập ứng dụng
Tìm hiểu công thức tính diện tích xung quanh hình trụ với phương pháp giải chi tiết, dễ hiểu. Bài viết gồm công thức cơ bản, ví dụ minh họa và bài tập thực hành có lời giải.

Công thức tính diện tích hình trụ và bài tập ứng dụng có đáp án
Hướng dẫn công thức tính diện tích hình trụ từ cơ bản đến nâng cao với các ví dụ minh họa chi tiết. Tìm hiểu cách tính diện tích đáy, xung quanh và toàn phần của hình trụ tròn xoay.

Hướng dẫn chi tiết công thức tính mét khối m3 và cách quy đổi đơn vị thể tích
Tìm hiểu công thức tính mét khối m3 đơn giản cho hình hộp, hình trụ. Hướng dẫn quy đổi sang lít, kg và ứng dụng tính thể tích bể nước, gỗ, bê tông trong thực tế.

Tổng hợp các công thức tính thể tích hình cầu và bài tập áp dụng có lời giải
Tìm hiểu công thức tính thể tích hình cầu đơn giản qua các ví dụ thực tế. Hướng dẫn chi tiết cách tính theo bán kính, đường kính kèm bài tập mẫu dễ hiểu cho học sinh.

Lý thuyết công thức thể tích khối tròn xoay và phương pháp giải chi tiết cho học sinh
Tìm hiểu chi tiết công thức thể tích khối tròn xoay với hướng dẫn tính toán đơn giản. Bao gồm các trường hợp quanh trục tọa độ, ví dụ minh họa và bài tập có lời giải cụ thể.

