Công thức tính diện tích xung quanh hình nón và bài tập hướng dẫn chi tiết

Chúng ta cùng khám phá **công thức tính diện tích xung quanh hình nón** thông qua phương pháp giảng dạy đơn giản, dễ hiểu. Bài viết trình bày chi tiết các yếu tố cấu thành, cách áp dụng công thức với nhiều bài tập mẫu phù hợp cho học sinh có học lực trung bình. Các ví dụ thực tế giúp các em hình dung rõ hơn về hình nón trong cuộc sống.

Tìm hiểu về diện tích xung quanh hình nón và ý nghĩa trong thực tế

Diện tích xung quanh hình nón là phần diện tích mặt cong bao quanh thân hình nón, không bao gồm diện tích đáy. Khi trải phẳng mặt cong này ra, ta sẽ thu được một hình phẳng có dạng hình quạt tròn.

Bạn đang xem: Công thức tính diện tích xung quanh hình nón và bài tập hướng dẫn chi tiết

Công thức tính diện tích xung quanh hình nón được xác định bằng tích của số π (pi), bán kính đáy (r) và độ dài đường sinh (l):

S = πrl

Trong đó, đường sinh (l) là khoảng cách từ đỉnh hình nón đến một điểm bất kỳ trên đường tròn đáy. Công thức này có ý nghĩa quan trọng khi ta cần tính toán lượng vật liệu cần thiết để bao phủ bề mặt một vật hình nón.

Trong thực tế, kiến thức về diện tích xung quanh hình nón được ứng dụng rộng rãi trong nhiều lĩnh vực. Ví dụ như trong ngành may mặc, khi thiết kế váy xòe dạng nón, các nhà thiết kế cần tính toán chính xác diện tích vải cần dùng. Theo chia sẻ của nhà thiết kế Đỗ Mạnh Cường, để tạo nên một chiếc váy xòe hoàn hảo, việc tính toán diện tích vải theo hình nón là bước quan trọng nhất.

Một ứng dụng khác là trong kiến trúc, khi thiết kế mái nhà hình nón hoặc tháp chuông nhà thờ. Kiến trúc sư cần tính chính xác diện tích bề mặt để xác định số lượng ngói, tôn hoặc vật liệu phủ cần thiết. Điều này giúp tiết kiệm chi phí và đảm bảo tính thẩm mỹ cho công trình.

Các yếu tố cơ bản cần biết để tính diện tích xung quanh hình nón

Để tính chính xác công thức tính hình nón, chúng ta cần nắm vững các yếu tố hình học cơ bản. Khi nhìn vào một hình nón, ta có thể thấy nó được tạo thành từ một mặt đáy hình tròn và một mặt xung quanh cong. Mặt xung quanh này thực chất là diện tích hình quạt là gì khi được cuộn tròn lại.

Đường sinh và bán kính đáy của hình nón

Đường sinh của hình nón là đoạn thẳng nối từ đỉnh đến một điểm bất kỳ trên đường tròn đáy. Đường sinh có vai trò quan trọng vì nó chính là bán kính của hình quạt khi trải phẳng mặt xung quanh hình nón ra. Bán kính đáy là khoảng cách từ tâm đáy đến một điểm bất kỳ trên đường tròn đáy. Hai yếu tố này luôn tồn tại mối quan hệ chặt chẽ với nhau thông qua chiều cao của hình nón.

Chiều cao và góc tạo bởi đường sinh với mặt phẳng đáy

Chiều cao của hình nón là đoạn thẳng vuông góc từ đỉnh đến mặt phẳng đáy. Góc tạo bởi đường sinh với mặt phẳng đáy được gọi là góc nghiêng của hình nón. Khi góc này càng nhỏ, hình nón càng “nhọn” và ngược lại. Mối quan hệ giữa chiều cao và góc nghiêng giúp xác định độ “mập” hay “gầy” của hình nón, từ đó ảnh hưởng trực tiếp đến diện tích xung quanh của nó.

Công thức tính diện tích xung quanh của hình nón và cách áp dụng

Xem thêm : Hướng dẫn công thức tính đường sinh và cách xác định trong hình học không gian

Công thức tính diện tích xung quanh của hình nón được xác định bằng tích của nửa chu vi đáy và đường sinh. Công thức cụ thể là:

Sxq = πrl

Trong đó r là bán kính đáy và l là đường sinh của hình nón. Đây là công thức cơ bản mà các em cần ghi nhớ để giải các bài toán liên quan.

Phân tích các thành phần trong công thức

Để hiểu rõ công thức, chúng ta cần nắm vững ý nghĩa của từng thành phần. Số π (pi) là hằng số toán học có giá trị xấp xỉ 3,14. Bán kính đáy r là độ dài từ tâm đáy đến chu vi đáy. Đường sinh l là độ dài đoạn thẳng nối từ đỉnh hình nón đến một điểm bất kỳ trên chu vi đáy.

Tương tự như công thức diện tích xung quanh hình trụ, công thức diện tích xung quanh hình nón cũng liên quan đến chu vi đáy. Tuy nhiên, thay vì nhân với chiều cao như hình trụ, ta nhân với đường sinh của hình nón.

Các bước tính diện tích xung quanh hình nón

Bước 1: Xác định các yếu tố đã cho trong bài toán (bán kính đáy r, chiều cao h, đường sinh l)
Bước 2: Nếu thiếu đường sinh l, tính l theo công thức Pytago: l = √(r² + h²)
Bước 3: Áp dụng công thức Sxq = πrl để tính diện tích xung quanh

Bài tập mẫu 1: Tính diện tích xung quanh hình nón khi biết bán kính và chiều cao

Cho hình nón có bán kính đáy r = 3cm và chiều cao h = 4cm.
– Tính đường sinh: l = √(3² + 4²) = √25 = 5cm
– Tính diện tích xung quanh: Sxq = π × 3 × 5 = 47,1cm²

Bài tập mẫu 2: Tính diện tích xung quanh hình nón khi biết đường sinh và bán kính

Cho hình nón có bán kính đáy r = 6cm và đường sinh l = 10cm.
Áp dụng trực tiếp công thức: Sxq = π × 6 × 10 = 188,4cm²

Mối quan hệ giữa diện tích xung quanh và diện tích toàn phần hình nón

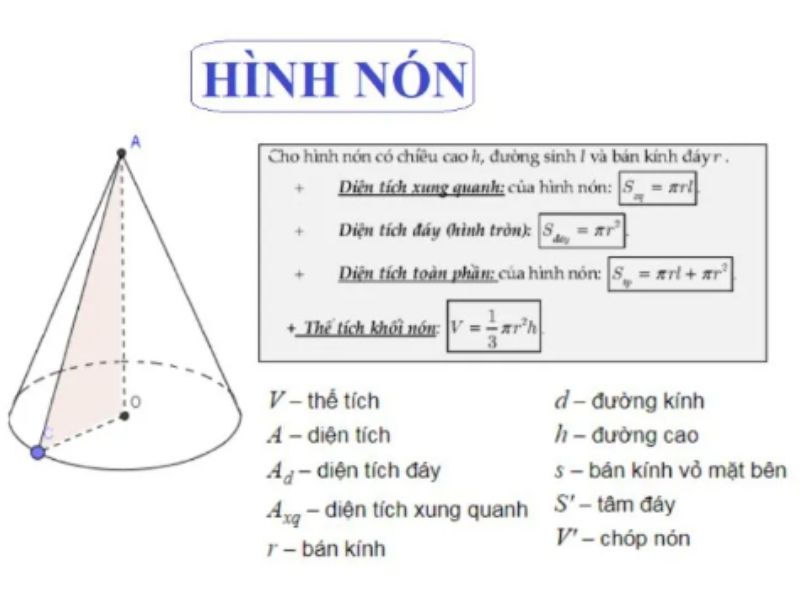
Diện tích xung quanh và diện tích toàn phần của hình nón có mối liên hệ mật thiết với nhau. Diện tích toàn phần bằng tổng của diện tích xung quanh và diện tích đáy. Tương tự như cách tính các hình phẳng khác như cách tính diện tích hình thoi, việc hiểu rõ mối quan hệ này sẽ giúp giải quyết nhiều bài toán phức tạp.

Công thức tính diện tích toàn phần hình nón

Công thức tính diện tích toàn phần của hình nón được xác định bằng công thức:

S = πr(r + l)

Trong đó:
– S là diện tích toàn phần
– r là bán kính đáy
– l là độ dài đường sinh
– π ≈ 3,14

Công thức trên có thể viết dưới dạng khác: S = πr² + πrl, với πr² là diện tích đáy và πrl là diện tích xung quanh. Việc nắm vững công thức sẽ giúp học sinh dễ dàng áp dụng vào các bài tập thực tế.

Bài tập mẫu: So sánh diện tích xung quanh và diện tích toàn phần

Cho hình nón có bán kính đáy r = 5cm và đường sinh l = 13cm. Công thức tính diện tích hình nón áp dụng như sau:

Diện tích xung quanh: Sxq = πrl = 3,14 × 5 × 13 = 204,1 cm²
Diện tích đáy: Sd = πr² = 3,14 × 5² = 78,5 cm²
Diện tích toàn phần: Stp = Sxq + Sd = 204,1 + 78,5 = 282,6 cm²

Xem thêm : Hướng dẫn chi tiết công thức tính mét khối m3 và cách quy đổi đơn vị thể tích

Qua kết quả tính toán, ta thấy diện tích xung quanh chiếm phần lớn diện tích toàn phần của hình nón, cụ thể là gấp khoảng 2,6 lần diện tích đáy.

Các dạng bài tập thường gặp về diện tích xung quanh hình nón

Khi học về công thức tính diện tích xung quanh hình nón, học sinh thường gặp nhiều dạng bài tập khác nhau. Mỗi dạng bài tập đều có những đặc điểm và cách giải riêng, đòi hỏi sự nắm vững kiến thức cơ bản và kỹ năng vận dụng công thức phù hợp.

Bài tập về tìm yếu tố chưa biết của hình nón

Dạng bài tập này yêu cầu học sinh tìm ra các yếu tố như chiều cao, bán kính đáy hay độ dài đường sinh khi biết diện tích xung quanh. Để giải được dạng bài này, cần nắm chắc mối quan hệ giữa các yếu tố trong hình nón. Ví dụ: Cho hình nón có diện tích xung quanh là 314 cm² và đường sinh dài 10 cm. Tính bán kính đáy của hình nón.

Ngoài ra, một số bài tập còn kết hợp với công thức tính thể tích khối nón để tạo thành các bài toán phức tạp hơn, giúp rèn luyện khả năng tư duy và phân tích.

Bài tập về so sánh diện tích xung quanh của các hình nón

So sánh diện tích xung quanh giữa các hình nón là dạng bài tập nâng cao, đòi hỏi học sinh phải biết phân tích và áp dụng các tính chất đồng dạng. Ví dụ: Cho hai hình nón có cùng chiều cao, bán kính đáy của hình nón thứ nhất gấp đôi bán kính đáy của hình nón thứ hai. So sánh diện tích xung quanh của hai hình nón.

Khi giải các bài toán so sánh, việc lập tỷ số giữa các diện tích xung quanh sẽ giúp đơn giản hóa phép tính và đưa ra kết luận chính xác.

FAQ: Câu hỏi thường gặp về diện tích xung quanh hình nón

Khi học về hình nón, nhiều học sinh thường gặp khó khăn và có những thắc mắc cần được giải đáp. Dưới góc độ một giáo viên với hơn 30 năm kinh nghiệm, tôi sẽ giải đáp những câu hỏi phổ biến nhất.

Làm sao để phân biệt diện tích xung quanh và diện tích toàn phần?

Diện tích xung quanh hình nón chỉ tính phần diện tích mặt cong của hình nón, giống như phần vỏ của chiếc nón lá. Còn diện tích toàn phần bao gồm cả phần mặt cong và diện tích đáy hình tròn. Một cách dễ hiểu, nếu bạn cắt một chiếc nón ra và trải phẳng, phần diện tích xung quanh chính là phần hình quạt tròn bạn nhìn thấy.

Tại sao cần học công thức tính diện tích xung quanh hình nón?

Công thức này có ý nghĩa thực tiễn rất lớn. Ví dụ khi may áo choàng, thiết kế ô dù, hay tính toán lượng vật liệu cần thiết để làm mái nhà hình nón. Trong công nghiệp, việc tính toán chính xác diện tích xung quanh của hình nón giúp tiết kiệm nguyên vật liệu và chi phí sản xuất.

Có những phương pháp nào để ghi nhớ công thức dễ dàng?

Cách tốt nhất để nhớ công thức là liên hệ với hình ảnh thực tế. Hãy tưởng tượng chiếc nón lá được trải phẳng ra thành hình quạt tròn. Chu vi đáy nhân với chiều cao tạo thành hình chữ nhật có diện tích bằng diện tích hình quạt. Do đó công thức πrs (với r là bán kính đáy, s là đường sinh) trở nên dễ hiểu hơn. Tôi thường ví von với học sinh rằng: “Giống như khi các con trải phẳng một chiếc nón giấy vậy!”

Việc áp dụng **công thức tính diện tích xung quanh hình nón** đòi hỏi sự hiểu biết chính xác về các yếu tố hình học cơ bản như đường sinh, bán kính đáy và chiều cao. Các công thức này có mối liên hệ chặt chẽ với diện tích toàn phần và được ứng dụng rộng rãi trong thực tế. Thông qua các bài tập mẫu và phương pháp giải chi tiết, học sinh có thể nắm vững kiến thức này một cách dễ dàng.

Nguồn: https://congthuctoan.com
Danh mục: Hình học không gian