Tổng quát công thức phương trình tiếp tuyến và các bài tập ứng dụng cụ thể

Các **công thức phương trình tiếp tuyến** đóng vai trò quan trọng trong việc nghiên cứu đặc điểm và tính chất của đường cong trong hình học. Bài viết trình bày chi tiết các công thức cơ bản, phương pháp xác định tiếp tuyến của đường tròn, parabol, elip cùng nhiều ví dụ minh họa giúp học sinh dễ dàng nắm vững kiến thức này.

Tiếp tuyến là gì và ý nghĩa của tiếp tuyến trong toán học?

Tiếp tuyến là gì? Đó là đường thẳng đi qua một điểm trên đường cong và có cùng hướng với đường cong tại điểm đó. Nói một cách dễ hiểu hơn, tiếp tuyến giống như một sợi chỉ thẳng “chạm khẽ” vào đường cong tại một điểm duy nhất và “nằm sát” với đường cong tại điểm chạm đó.

Bạn đang xem: Tổng quát công thức phương trình tiếp tuyến và các bài tập ứng dụng cụ thể

Để minh họa rõ hơn, các em hãy tưởng tượng khi đặt một cây thước thẳng chạm vào một vòng tròn. Nếu đặt sao cho thước chỉ chạm vào vòng tròn tại đúng một điểm, thì đường thẳng tạo bởi cạnh thước chính là tiếp tuyến của vòng tròn tại điểm chạm đó.

Tiếp tuyến có vai trò quan trọng trong toán học, đặc biệt trong hình học và giải tích. Nó giúp ta xác định độ dốc của đường cong tại một điểm, tính toán vận tốc tức thời của vật chuyển động, hay ứng dụng trong thiết kế các công trình kiến trúc. Ví dụ thực tế, khi thiết kế đường cao tốc, các kỹ sư thường sử dụng tiếp tuyến để tính toán độ cong của các khúc cua sao cho đảm bảo an toàn cho phương tiện di chuyển.

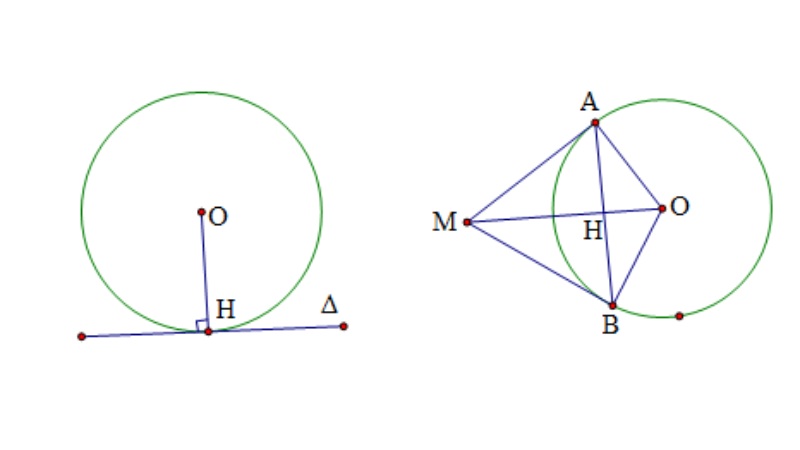
Trong thực tế, tiếp tuyến còn được ứng dụng rộng rãi trong nhiều lĩnh vực khác như vật lý (tính vận tốc, gia tốc), kinh tế (phân tích đồ thị tăng trưởng), hay thiết kế đồ họa (tạo đường cong mượt mà). Hiểu được bản chất của tiếp tuyến sẽ giúp các em nắm vững nhiều khái niệm quan trọng trong toán học và các môn học liên quan.

Các công thức phương trình tiếp tuyến cơ bản và cách áp dụng

Phương trình tiếp tuyến là một công cụ quan trọng trong hình học giải tích, giúp xác định đường thẳng tiếp xúc với đường cong tại một điểm. Để tìm được công thức phương trình tiếp tuyến, chúng ta cần nắm vững khái niệm đạo hàm và công thức tích có hướng của vector.

Phương trình tiếp tuyến tại một điểm cho trước

Khi xét một đường cong y = f(x), tiếp tuyến tại điểm M(x0, y0) có phương trình:

y – y0 = f'(x0)(x – x0)

Trong đó f'(x0) chính là hệ số góc của tiếp tuyến tại điểm M. Giá trị này cho biết độ dốc của đường thẳng tiếp xúc với đường cong tại điểm đang xét.

Bài tập mẫu về tìm phương trình tiếp tuyến tại điểm

Cho hàm số y = x² và điểm M(2,4). Ta tìm phương trình tiếp tuyến như sau:
– Tính đạo hàm: f'(x) = 2x
– Tại x0 = 2: f'(2) = 4
– Thay vào công thức: y – 4 = 4(x – 2)
– Kết quả: y = 4x – 4

Phương trình tiếp tuyến song song và vuông góc

Để cách tìm tiếp tuyến song song hoặc vuông góc với một đường thẳng cho trước, ta dựa vào mối quan hệ giữa các hệ số góc. Nếu hai đường thẳng song song, chúng có cùng hệ số góc. Nếu vuông góc, tích hệ số góc bằng -1.

Ví dụ minh họa về tiếp tuyến song song và vuông góc

Xem thêm : Tìm hiểu chi tiết công thức tính chu vi hình tam giác và các dạng bài tập thường gặp

Xét hàm số y = x³ và đường thẳng d: y = 2x + 1. Để tìm tiếp tuyến song song với d:

– Đạo hàm f'(x) = 3x²
– Tại điểm tiếp xúc: 3x² = 2 (vì song song nên hệ số góc bằng 2)
– Giải phương trình: x = ±√(2/3)
– Thay vào công thức tiếp tuyến ta được kết quả cuối cùng

Công thức tiếp tuyến của các đường cong cơ bản

Tiếp tuyến của đường cong là một khái niệm quan trọng trong hình học giải tích. Để xác định được tiếp tuyến, trước tiên cần nắm vững cách tìm tâm đường tròn và tính độ dài đoạn thẳng trong mặt phẳng. Các công thức tiếp tuyến đường tròn và công thức tiếp tuyến parabol sẽ được trình bày chi tiết dưới đây.

Tiếp tuyến của đường tròn và bài tập áp dụng

Tiếp tuyến của đường tròn là đường thẳng chỉ cắt đường tròn tại một điểm duy nhất gọi là tiếp điểm. Với đường tròn tâm O(a,b) bán kính R và điểm M(x0,y0) trên đường tròn, phương trình tiếp tuyến có dạng:

(x-a)(x0-a) + (y-b)(y0-b) = R^2

Ví dụ: Cho đường tròn (x-1)^2 + (y+2)^2 = 4 và điểm M(3,0). Tìm phương trình tiếp tuyến.
Giải: Ta có tâm O(1,-2), R = 2. Thay vào công thức: (x-1)(3-1) + (y+2)(0+2) = 4
⇒ 2(x-1) + 2(y+2) = 4 ⇒ x + y = 1

Tiếp tuyến của parabol và ví dụ minh họa

Với parabol y = ax^2 + bx + c, tiếp tuyến tại điểm M(x0,y0) có phương trình:

y = (2ax0 + b)(x – x0) + y0

Ví dụ: Tìm tiếp tuyến của parabol y = x^2 – 2x + 3 tại điểm có hoành độ x0 = 1
Giải: Tại x0 = 1, y0 = 1^2 – 2.1 + 3 = 2
Hệ số góc tiếp tuyến: 2ax0 + b = 2.1 – 2 = 0

Vậy phương trình tiếp tuyến: y = 0(x-1) + 2 ⇒ y = 2

Tiếp tuyến của elip và hypecbol

Với elip (x^2/a^2) + (y^2/b^2) = 1, tiếp tuyến tại điểm M(x0,y0) có phương trình:

(xx0/a^2) + (yy0/b^2) = 1

Với hypecbol (x^2/a^2) – (y^2/b^2) = 1, tiếp tuyến tại điểm M(x0,y0) có phương trình:
(xx0/a^2) – (yy0/b^2) = 1

Bài tập về tiếp tuyến elip và hypecbol

Cho elip (x^2/9) + (y^2/4) = 1 và điểm M(3,0). Tìm phương trình tiếp tuyến.
Giải: Thay M(3,0) vào công thức: (3x/9) + (0y/4) = 1
⇒ x = 3 là phương trình tiếp tuyến

Phương pháp xác định tiếp tuyến của các hàm số đặc biệt

Việc xác định tiếp tuyến của đồ thị hàm số đóng vai trò quan trọng trong việc nghiên cứu tính chất và ứng dụng của hàm số. Để tìm được tiếp tuyến, chúng ta cần nắm vững công thức tính lũy thừa và các quy tắc đạo hàm cơ bản. Trong một số trường hợp, việc áp dụng công thức đường trung tuyến cũng giúp đơn giản hóa quá trình tính toán.

Tiếp tuyến của hàm số mũ và logarit

Khi xác định tiếp tuyến của hàm mũ và logarit, điều quan trọng nhất là nắm vững công thức đạo hàm của chúng. Với hàm mũ y = ax, đạo hàm y’ = ax.ln(a). Còn với hàm logarit y = loga(x), đạo hàm y’ = 1/(x.ln(a)). Từ đó áp dụng cách xác định tiếp tuyến thông qua phương trình đường thẳng

Xem thêm : Hướng dẫn chi tiết công thức tính đường chéo hình chữ nhật và bài tập áp dụng

y – y0 = y'(x0)(x – x0)

Ví dụ về tìm tiếp tuyến hàm số mũ

Xét hàm số y = 2x tại điểm có hoành độ x0 = 1. Ta có y0 = 21 = 2 và y’ = 2x.ln(2). Tại x0 = 1, y'(1) = 2.ln(2). Vậy phương trình tiếp tuyến là: y – 2 = 2ln(2)(x – 1).

Bài tập về tiếp tuyến hàm logarit

Cho hàm số y = ln(x). Tìm tiếp tuyến tại điểm có hoành độ x0 = 1. Ta có y0 = ln(1) = 0 và y’ = 1/x. Tại x0 = 1, y'(1) = 1. Phương trình tiếp tuyến là: y = x – 1.

Tiếp tuyến của hàm số lượng giác

Các hàm lượng giác có tính tuần hoàn và đặc trưng riêng, đòi hỏi sự thận trọng khi tìm tiếp tuyến. Đạo hàm của sin(x) là cos(x), của cos(x) là -sin(x), và của tan(x) là 1/cos2(x).

Phương pháp tìm tiếp tuyến hàm sin, cos, tan

Với hàm y = sin(x), muốn tìm tiếp tuyến tại một điểm, ta cần xác định giá trị của sin(x0) và cos(x0). Ví dụ tại x0 = π/6, ta có y0 = 1/2 và y'(π/6) = cos(π/6) = √3/2. Phương trình tiếp tuyến là: y – 1/2 = (√3/2)(x – π/6).

FAQ: Câu hỏi thường gặp về phương trình tiếp tuyến

• Làm thế nào để xác định điểm tiếp xúc của tiếp tuyến với đồ thị hàm số?

Điểm tiếp xúc là điểm có hoành độ x0 thỏa mãn phương trình f'(x0) = hệ số góc của tiếp tuyến. Sau khi tìm được x0, thay vào hàm số để có tung độ y0.

• Tại sao <strong>công thức phương trình tiếp tuyến</strong> lại có dạng y – y0 = f'(x0)(x – x0)?

Đây là dạng điểm – hệ số góc của đường thẳng, trong đó (x0,y0) là điểm tiếp xúc và f'(x0) chính là hệ số góc của tiếp tuyến tại điểm đó.

• Có thể áp dụng phương pháp tìm tiếp tuyến cho mọi hàm số không?

Chỉ áp dụng được cho các hàm số khả vi tại điểm cần tìm tiếp tuyến. Tương tự như cách tìm số hạng đầu cấp số cộng, ta cần xác định được các điều kiện cần và đủ.

• Khi nào tiếp tuyến song song với trục hoành?

Tiếp tuyến song song với trục hoành khi hệ số góc f'(x0) = 0, tức là tại điểm cực trị của hàm số.

• Làm sao để tìm tiếp tuyến vuông góc với một đường thẳng cho trước?

Tích hệ số góc của hai đường thẳng vuông góc bằng -1. Nếu đường thẳng có hệ số góc k, ta cần tìm điểm x0 sao cho f'(x0) = -1/k.

Việc nắm vững các **công thức phương trình tiếp tuyến** là nền tảng quan trọng trong học tập toán học. Các công thức này giúp học sinh hiểu được mối liên hệ giữa đạo hàm và hình học, từ đó áp dụng vào giải các bài toán về đường thẳng, đường tròn, parabol và các đường cong khác. Thông qua các ví dụ minh họa và bài tập thực hành, kiến thức về tiếp tuyến trở nên dễ hiểu và thiết thực hơn trong việc học toán. Các phương pháp xác định tiếp tuyến đã được trình bày chi tiết giúp người học có thể tự tin giải quyết nhiều dạng toán khác nhau.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng