Các công thức tính đường kính hình tròn và mẹo làm bài tập đơn giản

Thầy giáo Toán với hơn 30 năm kinh nghiệm giảng dạy hướng dẫn chi tiết **công thức tính đường kính hình tròn** qua các phương pháp đơn giản và dễ hiểu nhất. Bài viết trình bày đầy đủ các trường hợp tính đường kính từ cơ bản đến nâng cao kèm ví dụ minh họa cụ thể giúp học sinh dễ dàng áp dụng vào bài tập thực tế.

Đường kính hình tròn là gì và tầm quan trọng của nó trong hình học?

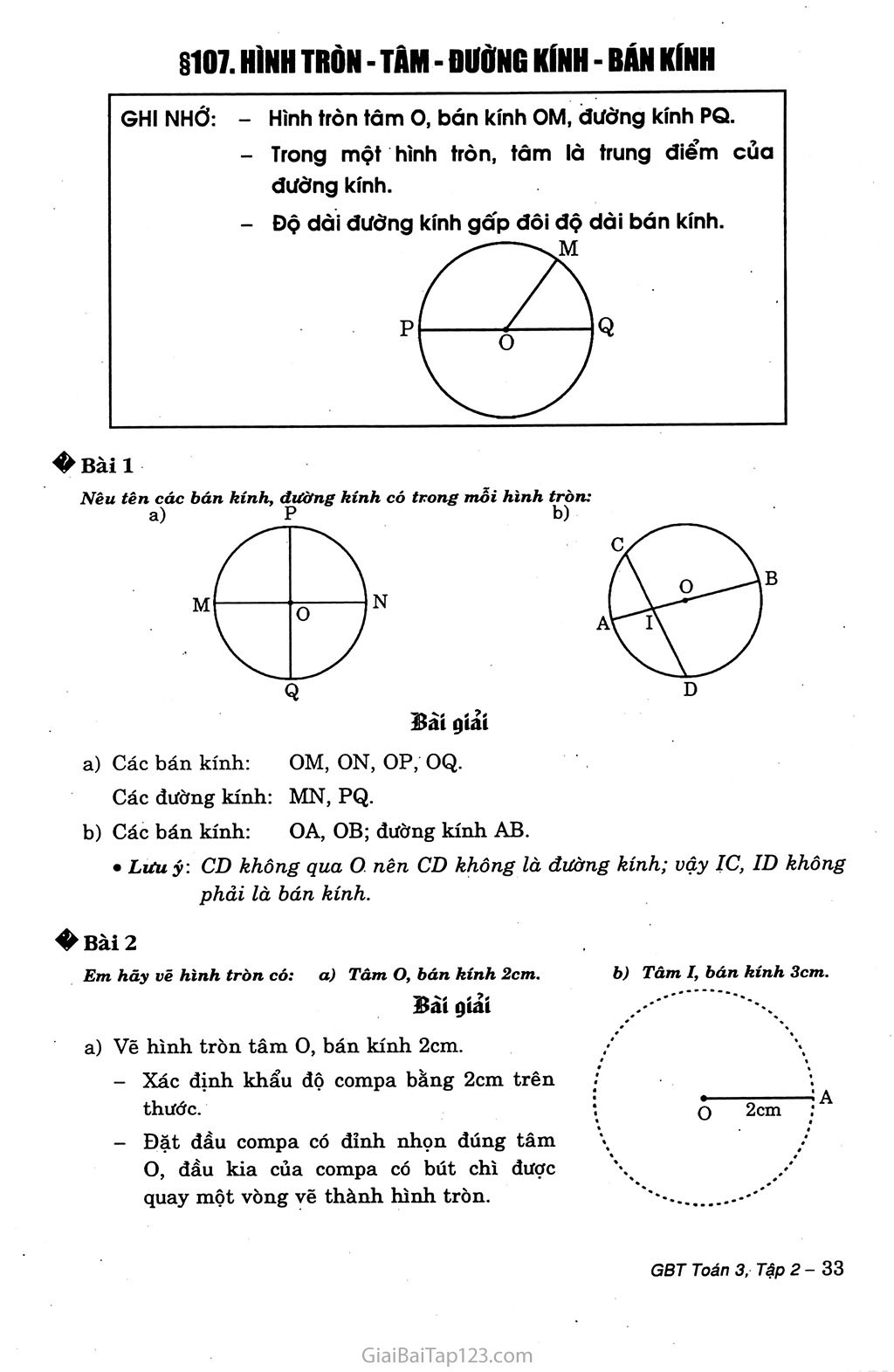
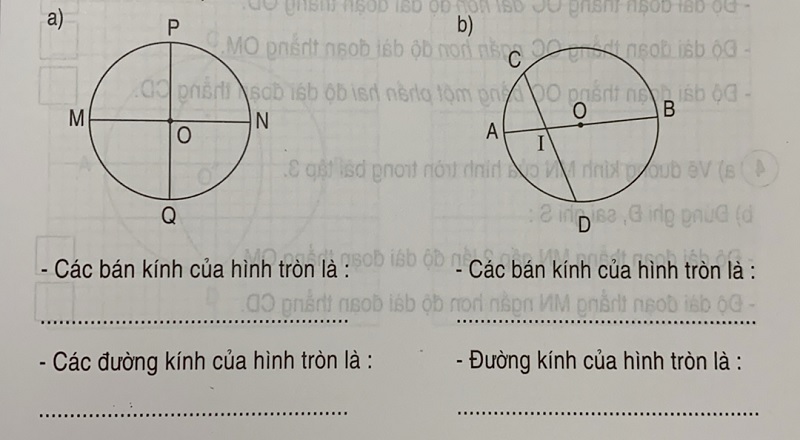
Đường kính hình tròn là đoạn thẳng đi qua tâm và nối hai điểm bất kỳ trên đường tròn. Nó là dây cung dài nhất của hình tròn và chia hình tròn thành hai phần bằng nhau. Mỗi hình tròn có vô số đường kính khác nhau nhưng tất cả đều bằng nhau về độ dài.

Bạn đang xem: Các công thức tính đường kính hình tròn và mẹo làm bài tập đơn giản

Đường kính đóng vai trò quan trọng trong việc xác định kích thước và tính chất của hình tròn. Nó có mối quan hệ mật thiết với công thức tính bán kính hình tròn, khi đường kính luôn gấp đôi bán kính. Điều này giúp chúng ta dễ dàng chuyển đổi qua lại giữa hai đại lượng này trong các bài toán thực tế.

Trong thực tế, đường kính được ứng dụng rộng rãi trong nhiều lĩnh vực. Ví dụ như khi đo đường ống nước, bánh xe, hay đường kính của một cái cốc. Theo nghiên cứu của Viện Khoa học và Công nghệ Việt Nam, việc xác định chính xác đường kính ống dẫn nước giúp tối ưu hóa được áp lực nước và tiết kiệm chi phí lắp đặt đến 15%.

Các công thức tính đường kính hình tròn cơ bản và phổ biến nhất

Để tính đường kính hình tròn, chúng ta có thể sử dụng nhiều phương pháp khác nhau dựa trên các yếu tố đã biết như bán kính, chu vi hoặc diện tích. Công thức tính đường kính hình tròn sẽ thay đổi tùy thuộc vào dữ kiện được cung cấp.

Mối quan hệ giữa đường kính và bán kính hình tròn

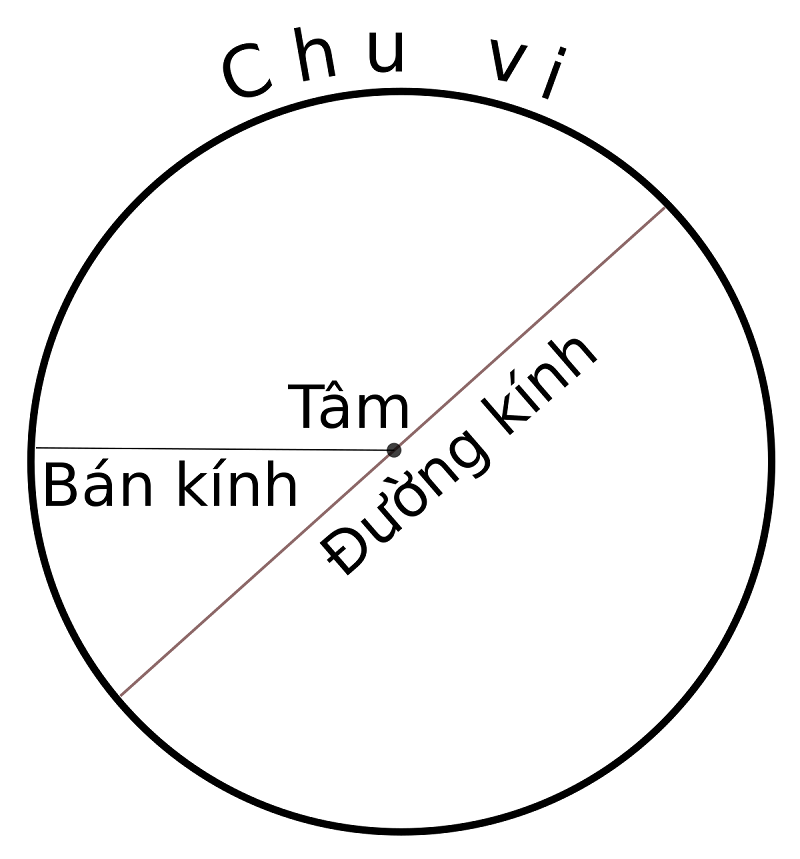
Đường kính là đoạn thẳng đi qua tâm và nối hai điểm bất kỳ trên đường tròn. Bán kính là đoạn thẳng nối tâm với một điểm trên đường tròn. Do đó, đường kính bằng hai lần bán kính, được biểu diễn bằng công thức:

d = 2r

(với d là đường kính, r là bán kính).

Công thức tính đường kính hình tròn qua chu vi

Cách tính đường kính hình tròn từ chu vi dựa vào mối quan hệ giữa chu vi hình tròn là gì và đường kính. Công thức:

d = C/π (với C là chu vi, π ≈ 3,14)

Ví dụ tính đường kính khi biết chu vi

Một bánh xe có chu vi đo được là 157 cm. Áp dụng công thức d = C/π, ta có:
d = 157/3,14 = 50 cm
Vậy đường kính bánh xe là 50 cm.

Công thức tính đường kính hình tròn qua diện tích

Khi biết công thức tính diện tích hình tròn, ta có thể tìm đường kính theo công thức:

d = 2√(S/π) (với S là diện tích)

Bài tập mẫu tính đường kính từ diện tích cho trước

Một đĩa tròn có diện tích 78,5 cm². Tính đường kính đĩa.

Giải:
d = 2√(78,5/3,14)
d = 2√25
d = 2 × 5 = 10 cm
Vậy đường kính đĩa tròn là 10 cm.

Tính đường kính đường tròn trong các trường hợp đặc biệt

Xem thêm : Áp dụng công thức tính diện tích hình thoi và cách giải bài tập chi tiết

Đường kính đường tròn có thể được tính theo nhiều cách khác nhau tùy thuộc vào các yếu tố đã biết. Việc nắm vững các công thức tính đường kính sẽ giúp giải quyết nhiều bài toán hình học phức tạp.

Công thức tính đường kính đường tròn ngoại tiếp tam giác

Công thức tính đường kính đường tròn ngoại tiếp tam giác được xác định thông qua diện tích và các cạnh của tam giác. Để tính chính xác, ta có thể sử dụng công thức tính bán kính đường tròn ngoại tiếp rồi nhân đôi kết quả.

Ví dụ minh họa cách tính đường kính đường tròn ngoại tiếp

Giả sử có tam giác ABC với các cạnh a = 6cm, b = 8cm, c = 10cm. Áp dụng công thức, ta có:
– Tính nửa chu vi p = (a + b + c)/2 = 12cm
– Diện tích S = √(p(p-a)(p-b)(p-c)) = 24cm²
– Đường kính D = abc/4S = 10cm

Đường kính đường tròn nội tiếp tam giác và cách tính

Đường kính đường tròn nội tiếp tam giác phụ thuộc vào diện tích và chu vi của tam giác. Khi áp dụng phương trình đường tròn tổng quát, ta cần xác định tâm và bán kính trước.

Bài tập có lời giải về đường tròn nội tiếp

Cho tam giác ABC có diện tích 60cm² và chu vi 36cm. Tính đường kính đường tròn nội tiếp:
D = 2r = 4S/p = 4×60/36 = 6.67cm

Tính đường kính đường tròn qua dây cung

Khi biết độ dài dây cung và khoảng cách từ tâm đến dây, ta có thể xác định đường kính thông qua định lý Pythagoras. Công thức áp dụng:

D = √(4h² + d²)

Với h là khoảng cách từ tâm đến dây và d là độ dài dây cung.

Ví dụ tính đường kính khi biết độ dài dây cung

Cho dây cung AB = 8cm và khoảng cách từ tâm đến dây h = 3cm.

Ta có: D = √(4×3² + 8²) = √(36 + 64) = √100 = 10cm

Các trường hợp đặc biệt khi tính đường kính đường tròn

Khi tính đường kính đường tròn, có những trường hợp đặc biệt liên quan đến hình vuông mà chúng ta cần nắm vững. Việc hiểu rõ mối quan hệ giữa đường tròn và hình vuông sẽ giúp giải quyết nhiều bài toán phức tạp một cách đơn giản hơn.

Đường kính đường tròn nội tiếp hình vuông

Đường kính đường tròn nội tiếp hình vuông có mối quan hệ chặt chẽ với cạnh của hình vuông. Khi đường tròn tiếp xúc với 4 cạnh của hình vuông, đường kính của nó sẽ bằng cạnh của hình vuông. Điều này có thể được chứng minh thông qua công thức tính độ dài cung tròn và tính chất đối xứng của hình vuông.

Đường kính đường tròn ngoại tiếp hình vuông

Với đường tròn ngoại tiếp hình vuông, đường kính sẽ bằng độ dài đường chéo của hình vuông. Nếu gọi a là cạnh hình vuông, đường kính đường tròn ngoại tiếp sẽ bằng a√2. Điều này xuất phát từ định lý Pytago áp dụng cho tam giác vuông được tạo bởi hai cạnh kề và đường chéo hình vuông.

Bài tập thực hành có lời giải chi tiết

Xem thêm : Tổng hợp công thức tính cạnh tam giác vuông và các phương pháp giải toán cơ bản

Bài toán: Cho hình vuông cạnh 6cm. Tính đường kính đường tròn nội tiếp và ngoại tiếp hình vuông này.

Lời giải:

• Đường kính đường tròn nội tiếp:

– Đường kính = cạnh hình vuông = 6cm

• Đường kính đường tròn ngoại tiếp:

– Đường kính = 6√2 ≈ 8,49cm
– Cách tính: d = a√2 = 6√2

Kết quả trên minh họa rõ mối quan hệ giữa đường kính đường tròn và kích thước hình vuông trong cả hai trường hợp nội tiếp và ngoại tiếp.

FAQ: Câu hỏi thường gặp về cách tính đường kính hình tròn

Khi học về hình tròn, nhiều bạn học sinh thường gặp khó khăn trong việc tính toán các yếu tố liên quan đến công thức tính đường kính. Tôi sẽ giải đáp một số thắc mắc phổ biến nhất mà các em thường hỏi trong quá trình học tập.

Làm thế nào để tính đường kính khi chỉ biết diện tích hình tròn?

Để tính đường kính từ diện tích, chúng ta sử dụng công thức

S = πr²

Từ đó, ta có thể suy ra đường kính

D = 2r = 2√(S/π)

Ví dụ với diện tích S = 78,5cm², ta có D = 2√(78,5/3,14) = 10cm. Đây là cách tính đơn giản mà các em có thể áp dụng.

Có thể tính đường kính đường tròn từ độ dài cung không?

Việc tính đường kính từ độ dài cung cần thêm thông tin về góc ở tâm ứng với cung đó. Nếu biết độ dài cung l và góc ở tâm α (tính bằng độ), ta có công thức:

D = (l×360)/(α×π)

Tôi thường lấy ví dụ về bánh pizza để giúp học sinh dễ hình dung hơn.

Mối quan hệ giữa đường kính và chu vi hình tròn là gì?

Chu vi hình tròn luôn bằng π nhân với đường kính (C = πD). Ngược lại, nếu biết chu vi, ta có thể tính được đường kính bằng cách chia chu vi cho π (D = C/π). Quan hệ này rất quan trọng và thường xuyên được sử dụng trong các bài toán thực tế như tính chiều dài dây thừng cần để quây một khu vực hình tròn.

Các **công thức tính đường kính hình tròn** đóng vai trò nền tảng trong việc giải các bài toán hình học. Từ mối quan hệ với bán kính, chu vi và diện tích đến những trường hợp đặc biệt như đường tròn nội tiếp, ngoại tiếp tam giác – tất cả đều tuân theo những quy luật toán học chặt chẽ. Việc nắm vững các công thức này giúp các em học sinh dễ dàng áp dụng vào thực tế, từ những bài toán đơn giản đến phức tạp.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng