Tổng hợp công thức tính chu vi hình tròn và có bài tập mẫu minh họa

Thầy giáo toán với hơn 30 năm kinh nghiệm giảng dạy hướng dẫn chi tiết **công thức tính chu vi hình tròn** cùng các phương pháp giải bài tập từ cơ bản đến nâng cao. Bài học được thiết kế đơn giản, dễ hiểu với nhiều ví dụ minh họa cụ thể, giúp các em nắm vững kiến thức quan trọng này một cách nhanh chóng và hiệu quả.

Công thức tính chu vi hình tròn là gì và ứng dụng trong thực tế?

Công thức tính chu vi hình tròn là

Bạn đang xem: Tổng hợp công thức tính chu vi hình tròn và có bài tập mẫu minh họa

C = 2πR hoặc C = πD

Trong đó C là chu vi, R là bán kính, D là đường kính và π ≈ 3,14. Đây là một trong những công thức cơ bản nhất mà các em cần nắm vững khi học về hình tròn. Tôi thường ví von rằng chu vi hình tròn giống như độ dài của sợi dây thừng quấn quanh một chiếc bánh tròn vậy.

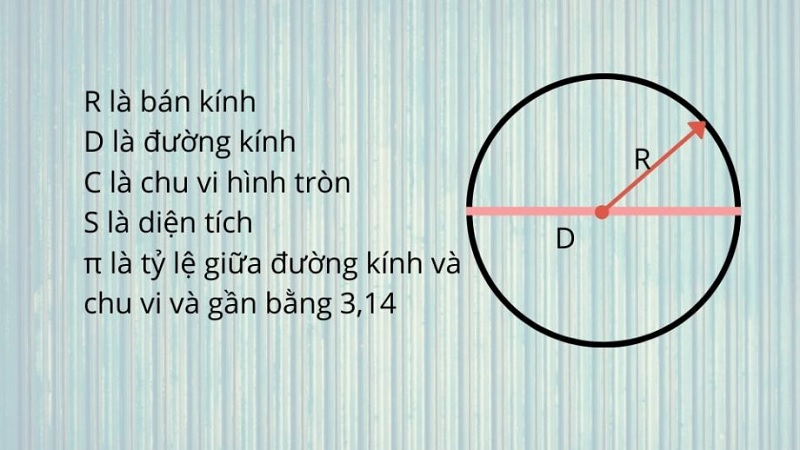
Công thức tính chu vi hình tròn là một công thức đơn giản nhưng có rất nhiều ứng dụng thực tiễn. Ví dụ như khi tính chiều dài của một đường chạy quanh sân vận động hình tròn, hay tính lượng dây cần thiết để làm khung cho một chiếc đèn lồng tròn. Tôi từng hướng dẫn một học sinh tính được chính xác số mét dây cần mua để làm hàng rào cho bể cá tròn trong sân trường, giúp tiết kiệm được chi phí mua vật liệu.

Khi học về chu vi hình tròn, các em cũng cần biết mối liên hệ giữa chu vi và diện tích hình tròn. Hai yếu tố này có mối quan hệ mật thiết với nhau thông qua bán kính R. Trong thực tế, việc nắm vững cả hai công thức sẽ giúp các em giải quyết được nhiều bài toán phức tạp hơn, như tính diện tích mặt nước của ao tròn khi biết chu vi, hay ngược lại.

Một ví dụ thực tế khác là khi làm bánh kem tròn, các đầu bếp thường dùng công thức này để tính độ dài của dải ruy băng trang trí viền bánh. Theo Chef John của Food Wishes, việc tính toán chính xác chu vi giúp họ chuẩn bị đủ nguyên liệu trang trí và tạo nên những chiếc bánh đẹp mắt, chuyên nghiệp.

Các thành phần cơ bản cần biết để tính chu vi hình tròn

Chu vi hình tròn là gì chính là độ dài của đường tròn bao quanh hình tròn. Để tính được chu vi hình tròn, chúng ta cần nắm vững hai thành phần quan trọng: bán kính (hoặc đường kính) và số Pi. Mỗi thành phần đều có vai trò riêng và ảnh hưởng trực tiếp đến kết quả tính toán.

Bán kính và đường kính trong hình tròn

Bán kính và đường kính là hai yếu tố không thể thiếu khi tính chu vi hình tròn. Đường kính hình tròn là gì sẽ bằng hai lần bán kính và đi qua tâm hình tròn. Công thức tính bán kính hình tròn giúp xác định khoảng cách từ tâm đến một điểm bất kỳ trên đường tròn. Khi biết một trong hai giá trị, ta có thể dễ dàng tìm ra giá trị còn lại.

Số Pi (π) và ý nghĩa trong công thức chu vi hình tròn

Số Pi là một hằng số toán học vô cùng quan trọng, có giá trị xấp xỉ 3,14. Số Pi thể hiện tỷ lệ giữa chu vi và đường kính của mọi hình tròn. Khi nhân số Pi với đường kính hoặc hai lần bán kính, ta sẽ có được chu vi của hình tròn. Đây là một hằng số không đổi và áp dụng cho tất cả các hình tròn, không phụ thuộc vào kích thước lớn hay nhỏ.

Hướng dẫn chi tiết cách tính chu vi hình tròn đơn giản và chính xác

Xem thêm : Tìm hiểu công thức tính bán kính đường tròn ngoại tiếp và bài tập áp dụng chi tiết

Để tính chu vi hình tròn một cách chính xác, bạn cần nắm vững hai công thức cơ bản dựa vào bán kính hoặc đường kính. Cách tính chu vi hình tròn sẽ trở nên đơn giản khi bạn hiểu rõ mối quan hệ giữa các yếu tố này.

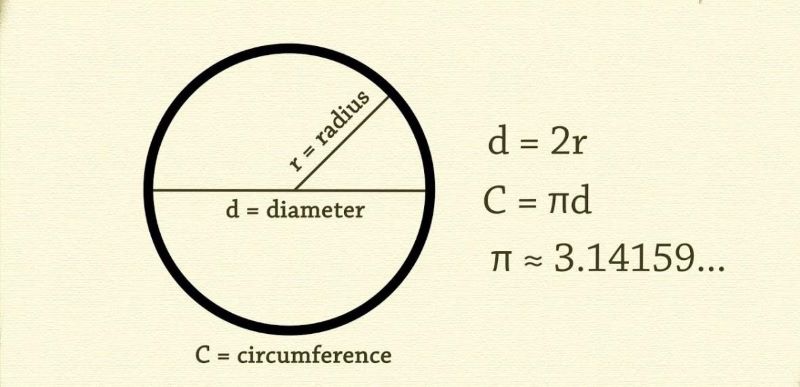
Công thức tính chu vi hình tròn khi biết bán kính

Công thức chu vi hình tròn khi biết bán kính R là:

C = 2πR

Trong đó π (pi) là hằng số có giá trị xấp xỉ 3,14. Với công thức này, bạn chỉ cần nhân đôi bán kính và nhân với π là có ngay kết quả. Tương tự như việc cách tính chu vi tam giác, việc ghi nhớ và áp dụng công thức sẽ giúp bạn giải quyết bài toán nhanh chóng.

Công thức tính chu vi hình tròn khi biết đường kính

Khi biết đường kính D, chu vi hình tròn đơn giản được tính theo công thức:

C = πD

Công thức này thực chất là rút gọn từ công thức trên vì đường kính bằng hai lần bán kính. Việc sử dụng công thức nào phụ thuộc vào dữ kiện cho trong bài toán.

Bài tập mẫu và phương pháp giải chi tiết

Ví dụ: Tính chu vi hình tròn có bán kính R = 5cm.

Giải:
– Áp dụng công thức C = 2πR
– Thay số: C = 2 × 3,14 × 5
– Tính toán: C = 31,4 (cm)

Khi làm bài tập, bạn nên kiểm tra kỹ đơn vị đo và làm tròn số thập phân theo yêu cầu. Với π, có thể lấy giá trị 3,14 hoặc 22/7 tùy theo độ chính xác cần thiết.

Các dạng bài tập thường gặp về chu vi hình tròn từ cơ bản đến nâng cao

Xem thêm : Công thức Pytago và bài tập minh họa

Việc nắm vững các dạng bài tập về chu vi hình tròn giúp học sinh phát triển tư duy toán học và khả năng giải quyết vấn đề thực tế. Tôi sẽ phân tích chi tiết từng dạng bài tập phổ biến để các em dễ dàng tiếp cận.

Bài tập tính chu vi hình tròn lớp 5

Ở cấp tiểu học, các bài tập tính chu vi hình tròn lớp 5 thường xuất hiện dưới dạng đơn giản, yêu cầu học sinh áp dụng công thức cơ bản C = 2πR. Giống như khi tính chu vi hình vuông bằng bao nhiêu, việc tính chu vi hình tròn cũng cần độ chính xác và cẩn thận.

Ví dụ: Một đĩa CD có bán kính 6cm. Tính chu vi đĩa CD.

Giải:
– Chu vi đĩa CD = 2 × 3,14 × 6 = 37,68 (cm)

Bài tập tính chu vi hình tròn lớp 9

Ở bậc THCS, chu vi hình tròn lớp 9 được nâng cao với nhiều dạng phức tạp hơn, đòi hỏi học sinh phải kết hợp kiến thức về đường tròn với các yếu tố hình học khác.

Phương pháp giải và lời giải chi tiết

Bài tập 1: Cho hình tròn có diện tích 78,5cm². Tính chu vi hình tròn.
Giải:

• Từ diện tích, tìm bán kính: S = πR²

R = √(S/π) = √(78,5/3,14) = 5 (cm)

• Tính chu vi: C = 2πR = 2 × 3,14 × 5 = 31,4 (cm)

Bài tập 2: Một bánh xe đạp có chu vi hình tròn 188,4cm. Tính số vòng quay của bánh xe khi xe chạy được 1km.
Giải:

• Đổi đơn vị: 1km = 100.000cm

• Số vòng quay = 100.000 ÷ 188,4 ≈ 531 vòng

FAQ: Câu hỏi thường gặp về chu vi hình tròn

Các câu hỏi thường gặp về chu vi hình tròn luôn là vấn đề khiến nhiều học sinh băn khoăn. Tôi sẽ giải đáp những thắc mắc phổ biến nhất để giúp các em hiểu rõ hơn về khái niệm này.

Chu vi hình tròn và chu vi đường tròn có giống nhau không?

Chu vi hình tròn và chu vi đường tròn hoàn toàn giống nhau. Công thức chu vi đường tròn C = 2πR áp dụng cho cả hai trường hợp, vì đường tròn chính là đường biên của hình tròn. Giống như việc đo chiều dài đường viền bao quanh một chiếc đĩa tròn vậy.

Làm thế nào để tính chu vi vòng tròn khi không biết bán kính?

Khi không biết bán kính, ta vẫn có thể tính được công thức tính chu vi vòng tròn thông qua đường kính (D = 2R) hoặc diện tích (S = πR²). Nếu biết đường kính, áp dụng công thức C = πD. Nếu biết diện tích, ta có thể tìm bán kính qua công thức R = √(S/π), sau đó thay vào công thức chu vi. Tương tự như cách tính chu vi hình chữ nhật bằng gì, ta cần linh hoạt sử dụng các yếu tố đã biết.

Mối quan hệ giữa chu vi và diện tích hình tròn

Chu vi hình tròn bằng gì thì có mối liên hệ mật thiết với diện tích. Khi chu vi tăng lên, diện tích sẽ tăng theo hàm mũ hai. Điều này giải thích tại sao khi tăng bán kính lên 2 lần, chu vi tăng 2 lần nhưng diện tích tăng tới 4 lần. Đây là một quy luật quan trọng giúp giải quyết nhiều bài toán thực tế.

Việc áp dụng **công thức tính chu vi hình tròn** đóng vai trò quan trọng trong học tập và cuộc sống. Các yếu tố cơ bản như bán kính, đường kính và số Pi giúp học sinh dễ dàng tính toán chu vi của mọi hình tròn. Thông qua các bài tập từ cơ bản đến nâng cao cùng phương pháp giải chi tiết, kiến thức này trở nên thiết thực và dễ hiểu với mọi đối tượng học sinh các cấp.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng