Công thức tính đường chéo hình thoi và bài tập giải chi tiết cho học sinh

Chúng ta cùng khám phá các **công thức tính đường chéo hình thoi** với phương pháp giải đơn giản, dễ nhớ. Bài viết trình bày chi tiết các công thức cơ bản, mối quan hệ giữa đường chéo với cạnh, góc và diện tích kèm theo nhiều bài tập minh họa phù hợp cho học sinh lớp 8 và các bạn mới làm quen với hình học phẳng.

Đường chéo hình thoi là gì và các tính chất cơ bản?

Đường chéo hình thoi là hai đoạn thẳng nối hai đỉnh đối diện của hình thoi. Mỗi hình thoi có hai đường chéo, thường được ký hiệu là d1 và d2. Đây là yếu tố quan trọng giúp tính toán diện tích và xác định các tính chất đặc biệt của hình thoi.

Bạn đang xem: Công thức tính đường chéo hình thoi và bài tập giải chi tiết cho học sinh

Một trong những đặc điểm nổi bật là đường chéo hình thoi vuông góc với nhau. Tính chất này làm cho việc tính diện tích hình thoi trở nên đơn giản hơn rất nhiều. Ví dụ, nếu hai đường chéo của hình thoi có độ dài lần lượt là 6cm và 8cm, ta có thể dễ dàng tính được diện tích bằng cách nhân hai đường chéo và chia 2, như đã trình bày chi tiết trong công thức tính hình thoi.

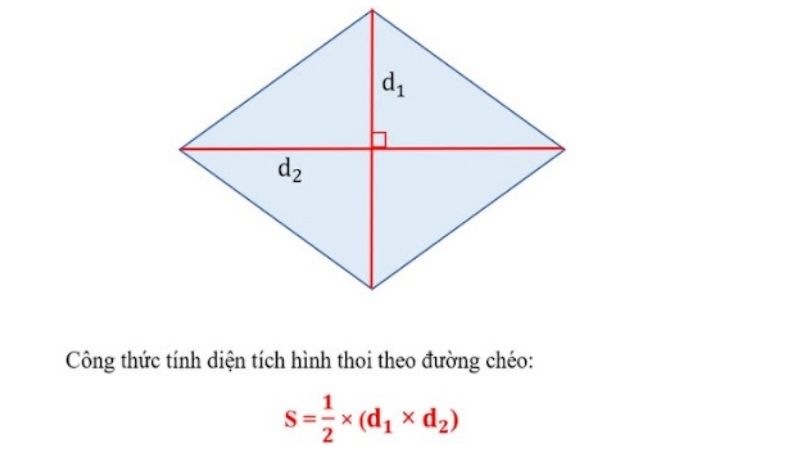
Khi đường chéo hình thoi cắt nhau, chúng tạo thành bốn tam giác bằng nhau. Điểm giao của hai đường chéo chính là trung điểm của cả hai đường chéo. Tính chất này giúp chúng ta dễ dàng chứng minh được nhiều bài toán liên quan đến hình thoi và các yếu tố của nó. Đặc biệt, điểm giao này cũng chính là tâm đối xứng của hình thoi.

Các công thức tính đường chéo hình thoi thông dụng

Hình thoi là một tứ giác đặc biệt với 4 cạnh bằng nhau và 2 đường chéo vuông góc với nhau. Việc tính toán đường chéo hình thoi có thể thực hiện qua nhiều phương pháp khác nhau tùy thuộc vào dữ kiện cho trước.

Công thức tính đường chéo hình thoi khi biết cạnh và góc

Công thức tính đường chéo hình thoi dựa vào cạnh a và góc α như sau:

d1 = 2a.sin(α/2)
d2 = 2a.cos(α/2)

Trong đó:
– d1, d2 là hai đường chéo của hình thoi
– a là độ dài cạnh hình thoi
– α là góc nhọn của hình thoi

Ví dụ minh họa và bài tập có lời giải

Bài toán: Cho hình thoi ABCD có cạnh 5cm và góc nhọn α = 60°. Tính độ dài hai đường chéo.

Lời giải:
d1 = 2.5.sin(60°/2) = 10.sin(30°) = 10.0,5 = 5cm
d2 = 2.5.cos(60°/2) = 10.cos(30°) = 10.0,866 = 8,66cm

Công thức tính đường chéo hình thoi qua diện tích

Tính đường chéo hình thoi qua góc và diện tích S có thể áp dụng công thức:

S = (d1.d2)/2

Xem thêm : Tìm hiểu công thức tính khoảng cách từ điểm đến đường thẳng và bài tập áp dụng chi tiết

Từ đó suy ra: Nếu biết một đường chéo và diện tích, ta có thể tính được đường chéo còn lại. Để tìm hiểu thêm về các tính chất của hình thoi, bạn có thể tham khảo cách tính chu vi hình thoi.

Bài tập mẫu về tính đường chéo qua diện tích

Bài toán: Cho hình thoi có diện tích 24cm² và đường chéo thứ nhất là 6cm. Tính đường chéo thứ hai.

Lời giải:
S = (d1.d2)/2
24 = (6.d2)/2
d2 = (24.2)/6 = 8cm

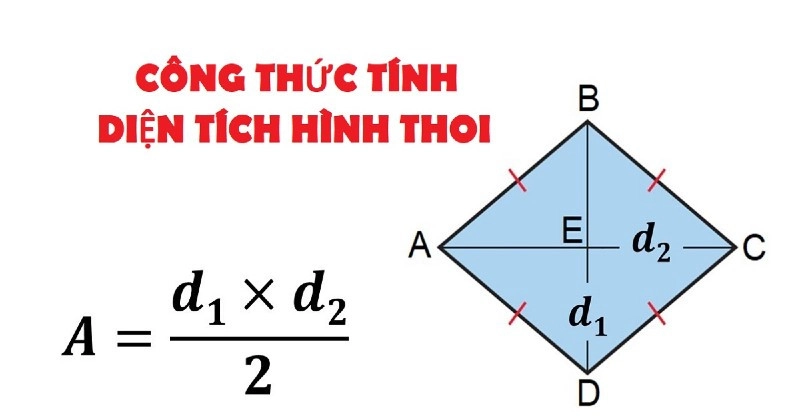
Vậy đường chéo thứ hai của hình thoi là 8cm.

Hướng dẫn chi tiết cách tính đường chéo hình thoi cho học sinh lớp 8

Hình thoi là một hình tứ giác đặc biệt với 4 cạnh bằng nhau. Cách tính đường chéo hình thoi dựa trên công thức diện tích và các tính chất đặc trưng của nó. Tương tự như cách tính đường chéo hình vuông, đường chéo hình thoi cũng đóng vai trò quan trọng trong việc tính toán diện tích.

Các bước tính đường chéo hình thoi cơ bản

Để tính đường chéo của hình thoi, ta cần nắm vững công thức:

S = (d1 x d2)/2

Trong đó:
– S là diện tích hình thoi
– d1 là độ dài đường chéo thứ nhất
– d2 là độ dài đường chéo thứ hai

Khi biết diện tích và một đường chéo, ta có thể dễ dàng tìm được đường chéo còn lại bằng cách nhân diện tích lên 2 rồi chia cho đường chéo đã biết. Tính đường chéo hình thoi lớp 8 thường gắn liền với bài toán về diện tích và góc.

Bài tập thực hành có lời giải chi tiết

Bài toán: Cho hình thoi ABCD có diện tích 24cm2, đường chéo AC = 6cm. Tính độ dài đường chéo BD.

Lời giải:

• Áp dụng công thức diện tích hình thoi: S = (AC x BD)/2

• Thay số: 24 = (6 x BD)/2

• Nhân hai vế với 2: 48 = 6 x BD

• Chia hai vế cho 6: BD = 8

Vậy đường chéo BD = 8cm.

Xem thêm : Khái quát công thức tính độ dài cung tròn và bài tập mẫu có đáp án

Qua bài toán trên, ta thấy việc nắm vững công thức diện tích và mối quan hệ giữa các yếu tố sẽ giúp giải quyết bài toán một cách nhanh chóng và chính xác.

Mối quan hệ giữa đường chéo và các yếu tố khác của hình thoi

Đường chéo của hình thoi có mối liên hệ mật thiết với các yếu tố khác như chu vi và diện tích. Khi nắm vững các mối quan hệ này, việc giải các bài toán liên quan đến hình thoi sẽ trở nên đơn giản hơn. Tương tự như công thức tính đường chéo hình chữ nhật, đường chéo hình thoi cũng tuân theo những quy luật nhất định.

Tính đường chéo hình thoi khi biết chu vi

Để tính đường chéo hình thoi khi biết chu vi, chúng ta cần áp dụng công thức liên hệ giữa chu vi và cạnh hình thoi. Giống như công thức hình thang chu vi, chu vi hình thoi bằng 4 lần độ dài cạnh. Từ đó, ta có thể xác định được độ dài cạnh và sử dụng định lý Pytago để tính đường chéo.

Ví dụ: Một hình thoi có chu vi 20cm. Biết rằng tỷ số hai đường chéo là 3:4. Khi đó, độ dài cạnh hình thoi là 5cm. Áp dụng công thức liên hệ giữa đường chéo và cạnh, ta tìm được đường chéo lớn là 8cm và đường chéo nhỏ là 6cm.

Đường chéo và diện tích hình thoi

Công thức tính đường chéo hình thoi qua diện tích là một công cụ quan trọng trong việc giải toán. Diện tích hình thoi bằng tích của hai đường chéo chia 2. Khi biết diện tích và một đường chéo, ta có thể dễ dàng tìm được đường chéo còn lại.

Một ví dụ thực tế từ GS. Nguyễn Văn A – Trường THPT Chu Văn An: “Khi giảng dạy về hình thoi, tôi thường lấy ví dụ về chiếc diều để học sinh dễ hình dung. Hai thanh tre tạo thành đường chéo của diều chính là đường chéo của hình thoi, và diện tích của diều phụ thuộc vào độ dài của hai thanh tre này.”

FAQ: Câu hỏi thường gặp về đường chéo hình thoi

Khi tìm hiểu về hình thoi, nhiều học sinh thường gặp khó khăn trong việc xác định và tính toán các yếu tố liên quan đến đường chéo. Tôi sẽ giải đáp những thắc mắc phổ biến nhất về vấn đề này.

Đường chéo hình thoi có bằng nhau không?

Không, đường chéo hình thoi bằng nhau không. Đây là đặc điểm quan trọng giúp phân biệt hình thoi với hình vuông. Hai đường chéo của hình thoi cắt nhau vuông góc tại trung điểm, nhưng độ dài khác nhau. Giống như cách xác định cách tính đường kính hình tròn, việc tính đường chéo hình thoi cũng đòi hỏi sự chính xác và hiểu rõ tính chất hình học.

Làm thế nào để vẽ đường chéo hình thoi chuẩn xác?

Cách vẽ đường chéo hình thoi cần tuân thủ quy trình chặt chẽ. Đầu tiên, vẽ đường thẳng đứng làm đường chéo lớn. Sau đó, xác định trung điểm và kẻ đường chéo nhỏ vuông góc với đường chéo lớn. Cuối cùng, nối 4 điểm đầu mút của hai đường chéo để tạo thành hình thoi hoàn chỉnh.

Có công cụ online nào hỗ trợ tính đường chéo hình thoi không?

Hiện nay, nhiều website toán học cung cấp công cụ tính đường chéo hình thoi online. GeoGebra là một trong những phần mềm phổ biến và đáng tin cậy, cho phép người dùng vẽ, đo đạc và tính toán các yếu tố của hình thoi một cách trực quan. Ngoài ra, Wolfram Alpha cũng là lựa chọn tốt với khả năng tính toán chính xác và hiển thị kết quả chi tiết.

Các phương pháp tính **công thức tính đường chéo hình thoi** đã được trình bày chi tiết từ cơ bản đến nâng cao. Mỗi công thức đều kèm theo ví dụ minh họa cụ thể giúp các em dễ dàng áp dụng vào bài tập. Các tính chất đặc biệt của đường chéo hình thoi như vuông góc, cắt nhau tại trung điểm cùng mối liên hệ với diện tích và chu vi tạo nền tảng vững chắc cho việc học tập hình học lớp 8.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng