Chi tiết công thức tính chiều cao hình thang và phương pháp xác định chuẩn xác nhất

Các phương pháp xác định **công thức tính chiều cao hình thang** được trình bày chi tiết với nhiều trường hợp khác nhau. Thông qua các ví dụ minh họa cụ thể và bài tập thực hành, người học dễ dàng nắm vững cách áp dụng công thức vào giải các bài toán về hình thang trong chương trình phổ thông.

Chiều cao hình thang là gì và vai trò của nó trong hình học?

Chiều cao hình thang là khoảng cách vuông góc từ đường thẳng chứa đáy này đến đường thẳng chứa đáy kia của hình thang. Nói một cách dễ hiểu hơn, đó chính là đoạn thẳng ngắn nhất nối hai đáy song song của hình thang và vuông góc với hai đáy đó.

Bạn đang xem: Chi tiết công thức tính chiều cao hình thang và phương pháp xác định chuẩn xác nhất

Thầy thường ví von chiều cao hình thang giống như một cái cột chống giữa hai đáy song song. Nếu các em tưởng tượng hình thang như một chiếc cổng, thì chiều cao chính là độ cao của cổng đó. Chiều cao luôn vuông góc với hai đáy, giống như khi các em đứng thẳng người vậy.

Chiều cao đóng vai trò vô cùng quan trọng trong việc tính diện tích hình thang. Công thức tính hình thang sẽ không thể hoàn chỉnh nếu thiếu yếu tố chiều cao. Giống như việc muốn biết diện tích của một mảnh vườn hình thang, các em cần đo cả chiều dài hai cạnh song song và chiều cao của nó.

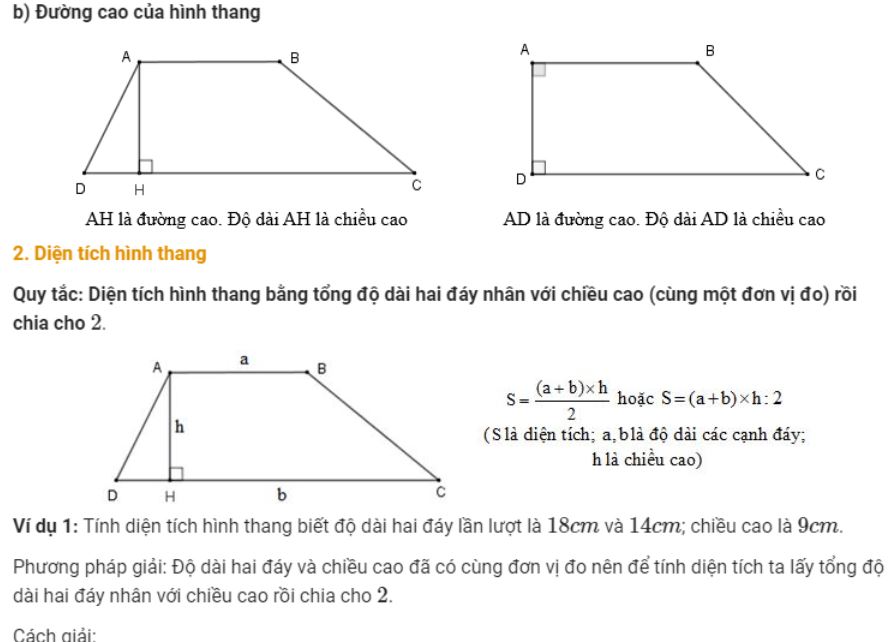
Khi giải các bài toán về hình thang, việc xác định chính xác chiều cao sẽ giúp các em tính toán dễ dàng và chính xác hơn. Đặc biệt trong các bài toán thực tế như tính diện tích mái nhà, diện tích mảnh đất hay thiết kế các công trình, chiều cao hình thang luôn là một yếu tố then chốt không thể bỏ qua.

Các phương pháp xác định và tính chiều cao hình thang cơ bản

Để xác định và tính chiều cao hình thang, chúng ta có thể áp dụng hai phương pháp chính. Mỗi phương pháp đều có ưu điểm riêng và phù hợp với từng bài toán cụ thể. Tương tự như chiều cao tam giác là gì, chiều cao hình thang cũng là khoảng cách vuông góc giữa hai đáy.

Phương pháp kẻ đường vuông góc từ đáy này đến đáy kia

Phương pháp đơn giản nhất để xác định chiều cao hình thang là kẻ một đường thẳng vuông góc từ đáy này đến đáy kia. Đường vuông góc này phải tạo với hai đáy một góc 90 độ. Độ dài của đoạn thẳng vuông góc đó chính là chiều cao của hình thang.

Khi thực hiện phép đo trực tiếp, cần đảm bảo thước kẻ hoặc compa tạo góc vuông chính xác. Một sai số nhỏ trong góc vuông có thể dẫn đến kết quả đo chiều cao không chính xác.

Phương pháp sử dụng công thức diện tích hình thang

Khi biết diện tích và độ dài hai đáy của hình thang, ta có thể tính cách tính chiều cao hình thang thông qua công thức diện tích:

Xem thêm : Hướng dẫn công thức tính cạnh tam giác thường và các trường hợp đặc biệt

S = h(a+b)/2

Trong đó S là diện tích, h là chiều cao, a và b là độ dài hai đáy. Từ đó, ta có thể biến đổi công thức để tìm h = 2S/(a+b).

Bài tập mẫu: Tính chiều cao hình thang khi biết diện tích và hai đáy

Cho hình thang có diện tích 24cm2, đáy lớn a = 8cm và đáy nhỏ b = 4cm. Áp dụng công thức h = 2S/(a+b), ta có:
h = 2 × 24/(8+4) = 48/12 = 4
Vậy chiều cao của hình thang là 4cm.

Công thức tính chiều cao hình thang trong các trường hợp đặc biệt

Chiều cao hình thang là khoảng cách vuông góc từ đáy này đến đáy kia. Tùy vào đặc điểm của từng loại hình thang mà có những cách tính chiều cao khác nhau. Việc nắm vững cách tính chiều cao hình thang vuông và chiều cao hình thang cân sẽ giúp bạn giải quyết nhiều bài toán liên quan đến chu vi hình thang là gì và diện tích hình thang.

Tính chiều cao hình thang vuông

Hình thang vuông có một cạnh bên vuông góc với hai đáy. Khi đó, cạnh bên vuông góc chính là chiều cao của hình thang. Để tính chiều cao, ta chỉ cần đo độ dài của cạnh bên vuông góc đó. Nếu biết tọa độ các đỉnh của hình thang vuông, ta có thể áp dụng công thức khoảng cách giữa hai điểm để tính chiều cao.

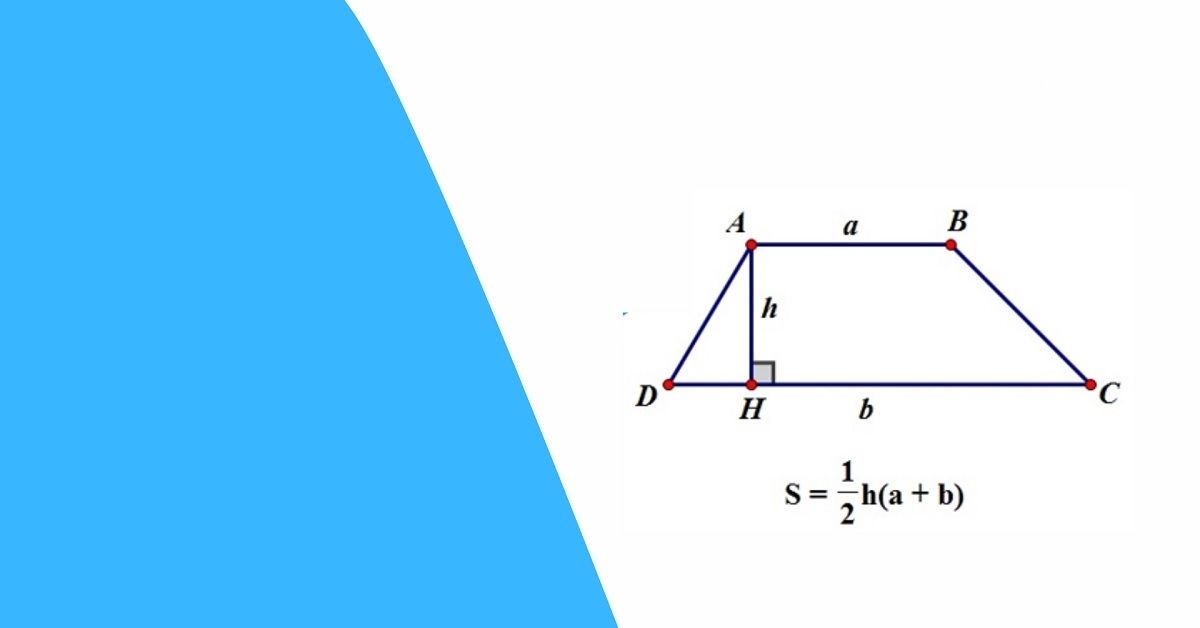
Xác định chiều cao hình thang cân

Với hình thang cân, hai cạnh bên bằng nhau và hai góc kề mỗi đáy bằng nhau. Chiều cao của hình thang cân được xác định bằng công thức Pytago khi biết độ dài cạnh bên và khoảng cách giữa hai đáy song song. Cụ thể, nếu gọi a là cạnh bên và d là nửa hiệu của hai đáy, chiều cao h được tính theo công thức:

h = √(a² – d²)

Ví dụ minh họa về cách tính chiều cao hình thang cân

Giả sử có một hình thang cân với cạnh bên dài 5cm, đáy lớn 8cm và đáy nhỏ 4cm. Ta tính chiều cao như sau:
– Nửa hiệu hai đáy: d = (8 – 4)/2 = 2cm
– Áp dụng công thức: h = √(5² – 2²) = √(25 – 4) = √21 ≈ 4,58cm

Kết quả cho thấy chiều cao của hình thang cân này xấp xỉ 4,58cm. Việc tính toán chính xác chiều cao giúp ta dễ dàng tính được diện tích và các yếu tố khác của hình thang.

Phương pháp tính chiều cao hình thang dựa trên các yếu tố cho trước

Xem thêm : Công thức hệ thức lượng trong tam giác đầy đủ và chi tiết

Chiều cao hình thang là yếu tố quan trọng để tính diện tích và các đặc điểm hình học khác. Tùy thuộc vào các yếu tố đã biết, có nhiều cách tiếp cận để tìm chiều cao hình thang một cách chính xác.

Tính chiều cao khi biết 4 cạnh của hình thang

Việc tính chiều cao hình thang khi biết 4 cạnh có thể thực hiện thông qua công thức tính diện tích và định lý Pitago. Giả sử ta có hình thang ABCD với đáy lớn a, đáy nhỏ b, hai cạnh bên c và d. Chiều cao h được tính bằng cách chia hình thang thành hai phần bằng đường cao, tạo thành hai tam giác vuông. Áp dụng công thức tính độ dài đoạn thẳng, ta có thể xác định được chiều cao h.

Tính chiều cao khi biết đường chéo hình thang

Khi tính chiều cao hình thang khi biết đường chéo, ta sử dụng mối quan hệ giữa đường chéo và các cạnh của hình thang. Tương tự như công thức tính diện tích hình thoi, diện tích hình thang cũng có thể tính qua đường chéo. Đường chéo chia hình thang thành hai tam giác, từ đó ta có thể thiết lập phương trình và giải ra chiều cao h.

Bài tập thực hành: Tìm chiều cao hình thang qua các yếu tố đã biết

Ví dụ 1: Cho hình thang ABCD có đáy lớn a = 10cm, đáy nhỏ b = 6cm, hai cạnh bên c = d = 5cm. Tính chiều cao h của hình thang.

Giải:
– Bước 1: Vẽ đường cao h từ đỉnh B xuống đáy AD
– Bước 2: Gọi BE = x là khoảng cách từ chân đường cao đến A
– Bước 3: Áp dụng định lý Pitago cho tam giác vuông BEA:
BE² + h² = c²
– Bước 4: Giải phương trình và tìm được h = 4cm

Qua bài tập trên, các em có thể thấy việc tìm chiều cao hình thang không quá phức tạp nếu nắm vững các bước giải và công thức cơ bản.

FAQ: Câu hỏi thường gặp về cách tính chiều cao hình thang

Việc tính toán chiều cao hình thang là một bài toán phổ biến nhưng không phải ai cũng nắm rõ các phương pháp giải quyết. Tôi sẽ giải đáp những thắc mắc thường gặp về vấn đề này.

Làm thế nào để tính chiều cao hình thang khi chỉ biết hai đáy?

Chỉ biết hai đáy thì không thể tính chiều cao hình thang khi biết 2 đáy. Cần thêm ít nhất một thông tin nữa như độ dài cạnh bên hoặc diện tích. Nếu biết độ dài cạnh bên, có thể áp dụng công thức tính độ dài vectơ để tìm chiều cao thông qua tam giác vuông.

Có thể tính chiều cao hình thang thông qua diện tích không?

Hoàn toàn có thể tính chiều cao hình thang qua diện tích. Khi biết diện tích (S) và hai đáy (a, b), áp dụng công thức S = h(a+b)/2, trong đó h là chiều cao. Từ đó suy ra h = 2S/(a+b). Ví dụ với diện tích 24cm2, đáy lớn 8cm và đáy nhỏ 4cm, chiều cao sẽ là: h = 2×24/(8+4) = 4cm.

Việc nắm vững các **công thức tính chiều cao hình thang** giúp học sinh giải quyết nhiều dạng toán hình học phổ thông. Chiều cao hình thang có thể được tính bằng nhiều phương pháp khác nhau tùy thuộc vào dữ kiện cho trước như diện tích, độ dài các cạnh hay đường chéo. Các công thức này áp dụng cho cả hình thang thường, hình thang vuông và hình thang cân với những đặc điểm riêng biệt.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng