Tìm hiểu công thức tính diện tích hình thang và bài tập mẫu có lời giải chi tiết

Thầy hướng dẫn chi tiết cách áp dụng **công thức tính diện tích hình thang** với các phương pháp đơn giản và dễ nhớ. Bài viết phân tích từng dạng hình thang cơ bản kèm ví dụ minh họa cụ thể, giúp học sinh nắm vững kiến thức và tự tin giải các bài toán về diện tích hình thang trong chương trình toán phổ thông.

Công thức tính diện tích hình thang là gì và ứng dụng trong thực tế?

Khi nhắc đến các hình học phẳng cơ bản, nhiều bạn học sinh thường nhầm lẫn giữa diện tích hình vuông là gì với các hình khác. Riêng với công thức tính diện tích hình thang, chúng ta có một công thức đơn giản:

Bạn đang xem: Tìm hiểu công thức tính diện tích hình thang và bài tập mẫu có lời giải chi tiết

Diện tích hình thang = (a + b) × h/2

Trong đó a, b là độ dài hai đáy song song và h là chiều cao hình thang.

Để dễ nhớ công thức này, tôi thường ví von với học sinh rằng hình thang giống như một chiếc bánh sandwich bị cắt nghiêng – hai đáy song song như hai lát bánh mì, còn chiều cao chính là độ dày của bánh. Khi tính diện tích, ta chỉ cần lấy tổng độ dài hai lát bánh nhân với nửa độ dày là ra kết quả.

Trong thực tế, công thức này được ứng dụng rất nhiều. Ví dụ như khi tính diện tích mảnh đất hình thang, diện tích mặt bên của máng nước, hay thậm chí là tính diện tích của các tấm biển quảng cáo có dạng hình thang. Một ví dụ cụ thể là các kỹ sư xây dựng thường sử dụng công thức này để tính diện tích mái nhà nghiêng có dạng hình thang để ước tính số lượng ngói cần thiết.

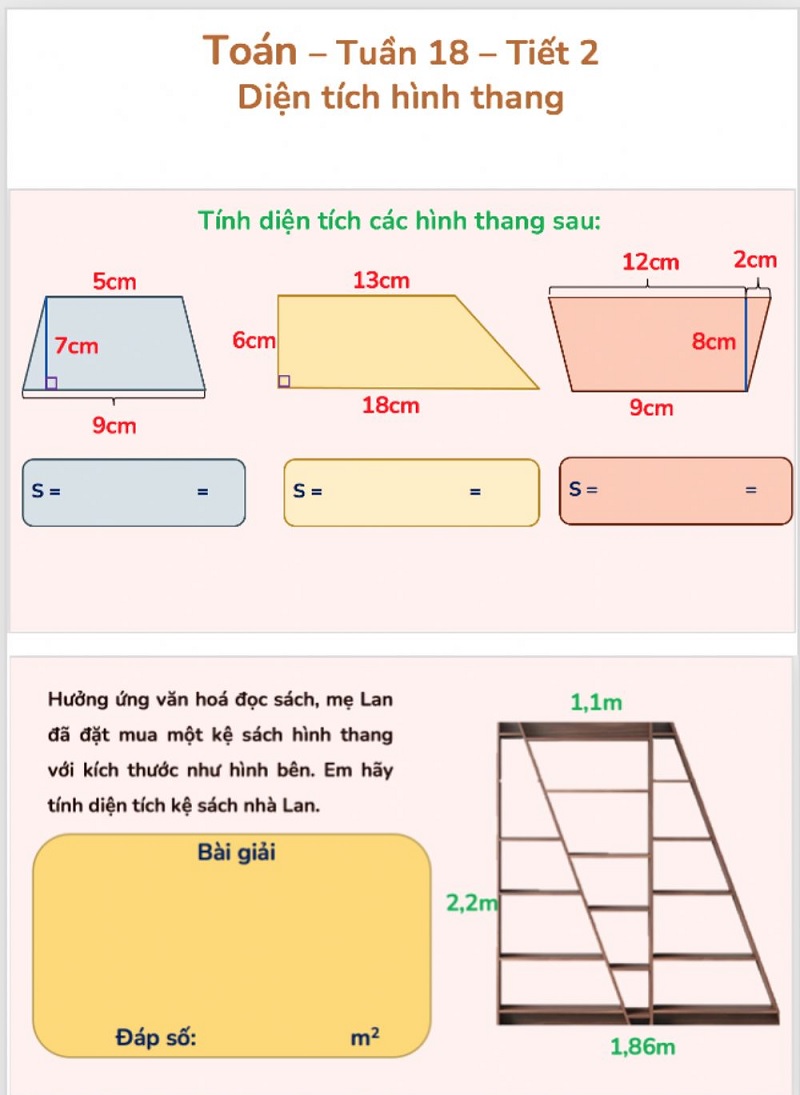
Một điểm quan trọng cần lưu ý là chiều cao h phải vuông góc với hai đáy song song. Nhiều học sinh thường nhầm lẫn khi đo cạnh bên thay vì đo chiều cao, điều này sẽ dẫn đến kết quả sai. Giống như khi đo chiều cao của một người, ta phải đo theo đường thẳng đứng, không phải đo theo đường xiên.

Các dạng hình thang cơ bản và công thức tính diện tích tương ứng

Hình thang là một tứ giác có hai cạnh song song. Dựa vào đặc điểm của các cạnh và góc, hình thang được phân thành 3 dạng cơ bản với các công thức tính diện tích khác nhau. Để tính toán chính xác diện tích, trước tiên cần xác định rõ loại hình thang và áp dụng đúng công thức phù hợp.

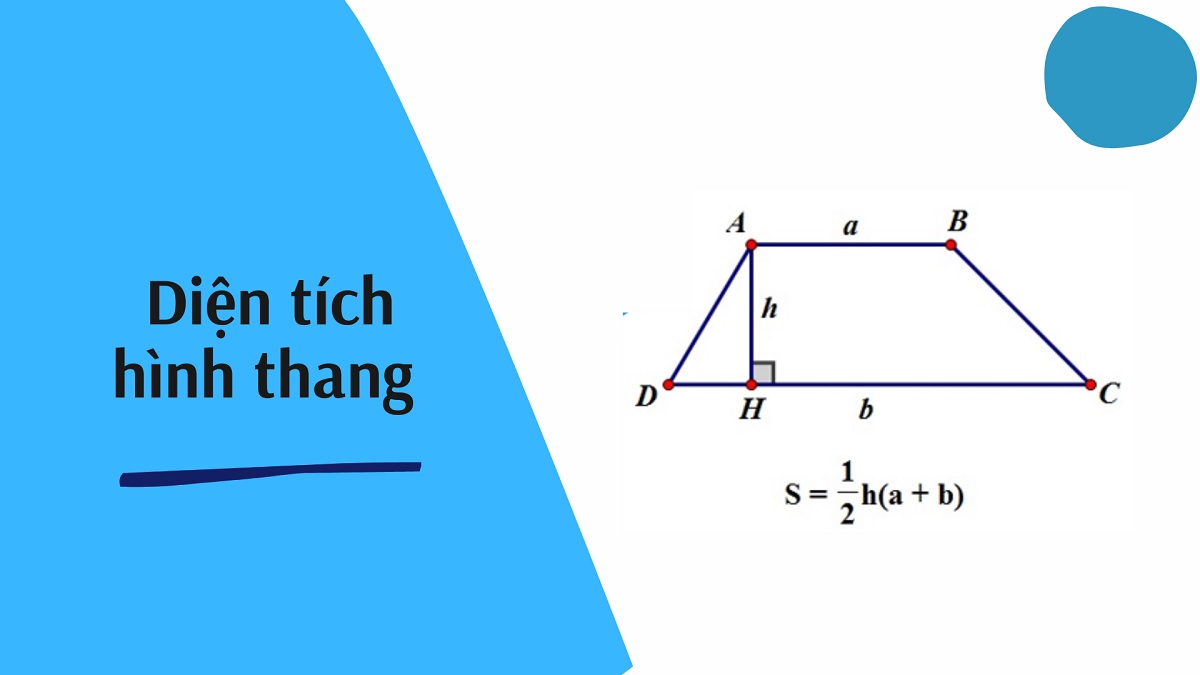
Công thức tính diện tích hình thang vuông và ví dụ minh họa

Công thức tính diện tích hình thang vuông được áp dụng khi một trong hai cạnh bên vuông góc với đáy. Diện tích hình thang vuông bằng tích của chiều cao với nửa tổng độ dài hai đáy:

S = h(a+b)/2

Trong đó h là chiều cao, a và b là độ dài hai đáy song song.

Ví dụ: Một mảnh đất hình thang vuông có đáy lớn 8m, đáy nhỏ 6m và chiều cao 5m. Áp dụng công thức ta có: S = 5(8+6)/2 = 35m2.

Công thức tính diện tích hình thang cân và bài tập áp dụng

Công thức tính diện tích hình thang cân cũng sử dụng công thức

S = h(a+b)/2

Xem thêm : Tổng hợp công thức tính chu vi hình tròn và có bài tập mẫu minh họa

Tuy nhiên cần lưu ý hai cạnh bên bằng nhau. Điều này giúp việc cách tính chu vi hình thang trở nên đơn giản hơn so với hình thang thường.

Bài tập: Một tấm biển quảng cáo hình thang cân có đáy lớn 4m, đáy nhỏ 2m, chiều cao 3m. Diện tích tấm biển là: S = 3(4+2)/2 = 9m2.

Công thức tính diện tích hình thang thường và các trường hợp đặc biệt

Hình thang thường không có các cạnh bên bằng nhau hoặc vuông góc với đáy. Công thức tính diện tích vẫn giữ nguyên

S = h(a+b)/2

Nhưng việc xác định chiều cao có thể phức tạp hơn do cần vẽ đường cao vuông góc với đáy.

Trường hợp đặc biệt: Khi biết tọa độ 4 đỉnh của hình thang, có thể sử dụng công thức tính diện tích qua tọa độ:

S = |x1(y2-y4) + x2(y3-y1) + x3(y4-y2) + x4(y1-y3)|/2

Hướng dẫn chi tiết cách tính diện tích hình thang khi biết các yếu tố

Việc tính diện tích hình thang có thể thực hiện qua nhiều phương pháp khác nhau tùy thuộc vào các yếu tố đã biết. Tôi sẽ hướng dẫn các em từng phương pháp một cách chi tiết và dễ hiểu nhất.

Tính diện tích hình thang khi biết 2 đáy và chiều cao

Công thức tính diện tích hình thang khi biết 2 đáy và chiều cao là:

S = ((a + b) × h)/2

Trong đó a, b là độ dài hai đáy và h là chiều cao. Nếu em chưa rõ về cách tính chiều cao hình thang, có thể tham khảo thêm.

Bài tập mẫu và lời giải chi tiết

Bài toán: Cho hình thang có đáy lớn a = 8cm, đáy nhỏ b = 6cm và chiều cao h = 4cm. Tính diện tích hình thang.

Giải:
– Áp dụng công thức: S = ((8 + 6) × 4)/2
– S = (14 × 4)/2 = 28 (cm²)

Tính diện tích hình thang khi biết 4 cạnh và đường cao

Cách tính diện tích hình thang dựa vào 4 cạnh và đường cao sẽ phức tạp hơn một chút. Ta cần kết hợp định lý Pytago để tìm chiều cao trước, sau đó áp dụng công thức cơ bản.

Xem thêm : Khám phá công thức tính diện tích hình vuông và bài tập từ cơ bản đến nâng cao

Ví dụ minh họa và các bước giải

Cho hình thang có đáy lớn a = 10cm, đáy nhỏ b = 6cm, hai cạnh bên c = d = 5cm.

Bước 1: Tính chiều cao bằng định lý Pytago
Bước 2: Thay vào công thức S = ((a + b) × h)/2

Tính diện tích hình thang khi biết đường chéo

Khi biết đường chéo, ta có thể chia hình thang thành hai tam giác và tính tổng diện tích của chúng.

Phương pháp giải và bài tập thực hành

Ví dụ: Hình thang có đường chéo d = 8cm chia hình thang thành hai tam giác có diện tích S₁ = 12cm² và S₂ = 16cm².
Diện tích hình thang = S₁ + S₂ = 28cm²

Các bài tập thực hành tính diện tích hình thang từ cơ bản đến nâng cao

Việc thực hành giải bài tập tính diện tích hình thang giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng tính toán. Tôi sẽ hướng dẫn các em từng bước với nhiều dạng bài tập khác nhau, kèm theo phương pháp giải chi tiết.

Bài tập cơ bản về diện tích hình thang vuông và cân

Bài tập 1: Cho hình thang vuông ABCD có đáy lớn AB = 8cm, đáy nhỏ DC = 5cm, chiều cao h = 4cm. Tính diện tích hình thang.

Bài tập 2: Cho hình thang cân MNPQ có hai đáy song song MN = 12cm và PQ = 6cm. Biết cạnh bên MP = 5cm. Tính diện tích hình thang.

Bài tập nâng cao về diện tích hình thang thường

Với các bài tập phức tạp hơn, học sinh cần kết hợp nhiều kiến thức như công thức tính diện tích hình thoi hay công thức tính diện tích hình quạt để giải quyết.

Bài tập 3: Cho hình thang ABCD có diện tích 48cm². Đường cao h = 6cm. Tỉ số đáy lớn và đáy nhỏ là 5:3. Tính độ dài hai đáy của hình thang.

Lời giải chi tiết và phương pháp làm bài hiệu quả

Bài tập 1:
– Áp dụng công thức tính hình thang: S = h(a+b)/2
– Thay số: S = 4(8+5)/2 = 26cm²

Bài tập 2:
– Tìm chiều cao bằng định lý Pytago
– h = √(5² – 3²) = 4cm
– S = 4(12+6)/2 = 36cm²

Bài tập 3:
– Gọi đáy nhỏ là x
– Đáy lớn sẽ là 5x/3
– Áp dụng công thức: 48 = 6(5x/3 + x)/2
– Giải phương trình tìm x = 9
– Vậy đáy nhỏ là 9cm, đáy lớn là 15cm

FAQ: Câu hỏi thường gặp về cách tính diện tích hình thang

• Làm sao để phân biệt đâu là đáy lớn, đáy bé của hình thang?

Đáy lớn là cạnh đáy dài hơn, đáy bé là cạnh đáy ngắn hơn. Bạn có thể dùng thước đo trực tiếp để so sánh độ dài 2 cạnh đáy.

• Có thể tính diện tích hình thang khi không biết chiều cao không?

Nếu không biết chiều cao nhưng biết độ dài 4 cạnh và 1 góc của hình thang, bạn có thể áp dụng công thức tính diện tích hình thang theo hệ số sin của góc.

• Tại sao công thức tính diện tích hình thang lại có dạng (a+b)h/2?

Vì hình thang có thể xem như tổng của 2 hình tam giác có cùng chiều cao h. Tương tự như công thức tính diện tích hình cầu, đây là công thức cơ bản cần ghi nhớ.

• Làm thế nào để đo chiều cao hình thang chính xác?

Chiều cao hình thang là khoảng cách ngắn nhất từ đáy này đến đáy kia. Bạn cần kẻ đường vuông góc với 2 đáy để đo chiều cao chính xác.

• Có cách nào kiểm tra kết quả tính diện tích hình thang đã đúng chưa?

Bạn có thể chia hình thang thành các hình tam giác, tính tổng diện tích các tam giác đó rồi so sánh với kết quả tính theo công thức hình thang.

Các phương pháp tính toán và **công thức tính diện tích hình thang** đã được trình bày chi tiết qua nhiều trường hợp khác nhau. Mỗi dạng bài tập đều có hướng giải cụ thể kèm ví dụ minh họa rõ ràng, giúp các em nắm vững kiến thức cơ bản. Việc thực hành nhiều bài tập từ đơn giản đến phức tạp sẽ tạo nền tảng vững chắc cho việc học tập toán hình học ở các cấp độ cao hơn.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng