Khám phá công thức tính diện tích hình vuông và bài tập từ cơ bản đến nâng cao

Bài toán về **công thức tính diện tích hình vuông** luôn xuất hiện trong chương trình toán phổ thông. Với phương pháp giảng dạy đơn giản, dễ hiểu cùng các ví dụ minh họa cụ thể, chúng tôi giúp các em nắm vững kiến thức này từ cơ bản đến nâng cao và vận dụng thành thạo vào thực tế.

Diện tích hình vuông là gì? Tìm hiểu khái niệm và đặc điểm cơ bản

Các em học sinh thân mến, khi nhắc đến hình vuông, chắc hẳn ai cũng nghĩ ngay đến một hình có 4 cạnh bằng nhau phải không? Nhưng để hiểu rõ về diện tích hình vuông là gì, chúng ta cần tìm hiểu sâu hơn một chút.

Bạn đang xem: Khám phá công thức tính diện tích hình vuông và bài tập từ cơ bản đến nâng cao

Diện tích hình vuông chính là phần không gian bên trong được giới hạn bởi 4 cạnh của hình vuông. Nói một cách dễ hiểu hơn, nếu các em có một mảnh giấy hình vuông, diện tích chính là toàn bộ phần bề mặt của mảnh giấy đó.

Thầy lấy ví dụ thực tế nhé: Khi các em muốn lát gạch cho một sân trường hình vuông, diện tích sân trường sẽ cho biết cần bao nhiêu viên gạch để phủ kín toàn bộ mặt sân. Giả sử mỗi viên gạch vuông có cạnh 40cm, sân trường có cạnh 10m, các em sẽ cần 625 viên gạch để lát kín sân.

Một đặc điểm quan trọng của hình vuông là tất cả các cạnh đều bằng nhau và các góc đều bằng 90 độ. Chính vì thế, chỉ cần biết độ dài một cạnh, các em có thể dễ dàng tính được diện tích của hình vuông. Đây là một ưu điểm lớn so với các hình học khác như hình chữ nhật hay hình thang.

Công thức tính diện tích hình vuông cơ bản và các trường hợp đặc biệt

Công thức tính diện tích hình vuông cơ bản là một trong những kiến thức nền tảng quan trọng trong hình học. Với tư cách là một giáo viên toán lâu năm, tôi luôn nhấn mạnh với học sinh rằng việc nắm vững công thức này sẽ giúp các em tự tin giải quyết nhiều bài toán phức tạp hơn sau này.

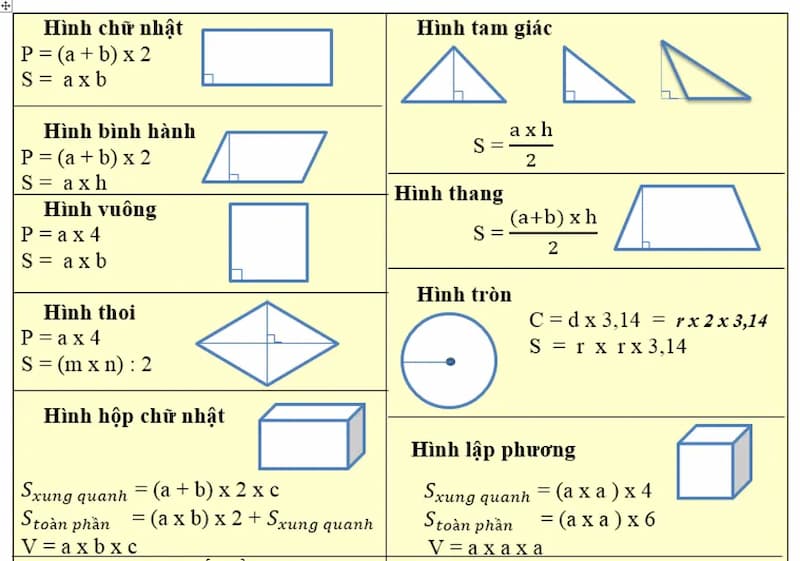
Công thức tính diện tích hình vuông khi biết độ dài cạnh

Khi biết độ dài cạnh a của hình vuông, diện tích S được tính bằng công thức:

S = a²

Đây là công thức đơn giản nhất mà các em cần ghi nhớ. Ngoài ra, các em có thể tham khảo thêm công thức tính chu vi hình vuông để có cái nhìn toàn diện về hình vuông.

Công thức tính diện tích hình vuông khi biết đường chéo

Với trường hợp biết độ dài đường chéo d của hình vuông, diện tích S được tính theo công thức:

Xem thêm : Công thức Pytago và bài tập minh họa

S = d²/2

Công thức này được rút ra từ mối quan hệ giữa cạnh và đường chéo trong hình vuông, áp dụng định lý Pytago.

Ví dụ minh họa về cách áp dụng công thức

Bài tập 1: Tính diện tích hình vuông khi biết cạnh

Một hình vuông có cạnh 5cm.
Áp dụng công thức S = a²
S = 5² = 25
Vậy diện tích hình vuông là 25cm²

Bài tập 2: Tính diện tích hình vuông khi biết đường chéo

Cho hình vuông có đường chéo 8cm.

Áp dụng công thức S = d²/2
S = 8²/2 = 64/2 = 32
Vậy diện tích hình vuông là 32cm²

Hướng dẫn chi tiết cách tính diện tích hình vuông cho học sinh lớp 5

Diện tích hình vuông được tính bằng cách lấy độ dài cạnh nhân với chính nó. Với công thức đơn giản

S = a × a

(trong đó a là độ dài cạnh), việc tính cách tính diện tích hình vuông trở nên dễ dàng cho học sinh lớp 5.

Các bước tính diện tích hình vuông

Để tính diện tích hình vuông, học sinh cần thực hiện theo trình tự:

• Xác định độ dài cạnh của hình vuông (thường được kí hiệu là a)

• Áp dụng công thức S = a × a

• Thực hiện phép nhân và ghi kết quả kèm đơn vị đo diện tích

Ví dụ: Một hình vuông có cạnh 5cm. Ta có:
– Độ dài cạnh a = 5cm
– Diện tích S = 5 × 5 = 25
– Kết quả: S = 25cm²

Bài tập mẫu có lời giải chi tiết

Tương tự như công thức tính diện tích hình chữ nhật, diện tích hình vuông lớp 5 cũng cần được làm quen qua các bài tập thực hành.

Bài toán về diện tích hình vuông trong đời sống

Bài toán: Một miếng đất hình vuông có cạnh 10m. Tính diện tích miếng đất.

Lời giải:
– Độ dài cạnh a = 10m
– Diện tích S = 10 × 10 = 100
– Kết quả: Diện tích miếng đất là 100m²

Bài toán về diện tích hình vuông trong hình học

Bài toán: Một hình vuông có chu vi 20cm. Tính diện tích hình vuông đó.

Lời giải:
– Chu vi hình vuông = 4 × cạnh = 20cm
– Độ dài cạnh = 20 ÷ 4 = 5cm
– Diện tích S = 5 × 5 = 25
– Kết quả: Diện tích hình vuông là 25cm²

Phương pháp giải các bài toán nâng cao về diện tích hình vuông

Xem thêm : Tìm hiểu công thức tính chu vi hình vuông và hướng dẫn giải bài tập từ cơ bản đến nâng cao

Các công thức tính diện tích hình vuông nâng cao thường xuất hiện trong những bài toán phức tạp, đòi hỏi sự kết hợp giữa nhiều kiến thức hình học. Tôi sẽ giúp các em phân tích từng dạng bài cụ thể để nắm vững phương pháp giải.

Bài toán về diện tích hình vuông có đường chéo

Diện tích hình vuông có đường chéo là dạng bài thường gặp. Khi có đường chéo, hình vuông được chia thành 2 tam giác vuông bằng nhau. Đường chéo hình vuông có tính chất đặc biệt: bằng cạnh hình vuông nhân với căn bậc hai của 2. Điều quan trọng là các em cần nhớ mối liên hệ giữa cạnh và đường chéo để giải nhanh các bài toán.

Bài toán về diện tích hình vuông và các hình khác

Khi kết hợp hình vuông với các hình khác, chúng ta cần vận dụng linh hoạt công thức tính diện tích hình tròn và diện tích hình chữ nhật công thức. Việc phân tích mối quan hệ giữa các hình là chìa khóa để giải thành công.

Ví dụ về diện tích hình vuông và hình tròn nội tiếp

Giả sử có một hình tròn nội tiếp hình vuông cạnh a. Bán kính hình tròn sẽ bằng a/2. Diện tích phần còn lại của hình vuông (phần không thuộc hình tròn) được tính bằng: a² – πr² = a²(1 – π/4). Công thức này rất hữu ích khi giải các bài toán tương tự.

Ví dụ về diện tích hình vuông và hình chữ nhật

Khi hình vuông và hình chữ nhật có quan hệ với nhau, ta thường áp dụng nguyên tắc so sánh diện tích. Ví dụ: nếu hình chữ nhật có chiều dài bằng cạnh hình vuông và chiều rộng bằng 1/2 cạnh hình vuông, diện tích hình chữ nhật sẽ bằng 1/2 diện tích hình vuông. Đây là cách tư duy cần thiết để giải các bài toán phức tạp.

FAQ: Câu hỏi thường gặp về diện tích hình vuông

Diện tích hình vuông là một kiến thức cơ bản nhưng rất quan trọng trong hình học. Các câu hỏi thường gặp sau sẽ giúp bạn hiểu rõ hơn về diện tích hình vuông đơn giản và các mối liên hệ của nó.

Làm sao để nhớ công thức diện tích hình vuông dễ dàng?

Để nhớ công thức diện tích hình vuông, bạn có thể liên tưởng đến việc lát gạch vuông. Khi lát một hàng gạch vuông cạnh a, ta cần a viên. Để lát thành hình vuông, ta cần lát a hàng như vậy. Vì thế diện tích hình vuông bằng bao nhiêu sẽ chính là a × a = a². Ngoài ra, bạn có thể tham khảo thêm công thức tính diện tích hình trụ để thấy sự tương đồng trong cách tính.

Tại sao diện tích hình vuông bằng bình phương cạnh?

Diện tích hình vuông bằng bình phương cạnh vì đây là hình có 4 cạnh bằng nhau và 4 góc vuông. Khi đo diện tích, ta cần tính số đơn vị diện tích hình vuông đơn vị lấp đầy hình. Do tính chất đặc biệt của hình vuông, số đơn vị theo chiều dài nhân với số đơn vị theo chiều rộng sẽ cho ta bình phương cạnh. Tương tự như cách tính công thức tính diện tích hình cầu, công thức này phản ánh đúng bản chất hình học.

Mối quan hệ giữa chu vi và diện tích hình vuông?

Mối quan hệ giữa chu vi và diện tích hình vuông thể hiện qua công thức: nếu chu vi là P thì cạnh a = P/4, và diện tích S = (P/4)². Ngược lại, nếu biết diện tích S thì cạnh a = √S và chu vi P = 4√S. Đây là mối quan hệ quan trọng giúp giải nhiều bài toán thực tế về hình vuông.

Các phương pháp tính toán và **công thức tính diện tích hình vuông** đã được trình bày một cách có hệ thống từ cơ bản đến nâng cao. Việc nắm vững công thức cơ bản S = a² và các trường hợp đặc biệt với đường chéo giúp học sinh giải quyết tốt các bài toán thực tế. Các ví dụ minh họa và bài tập mẫu đã chỉ ra cách áp dụng công thức một cách chính xác và hiệu quả trong nhiều tình huống khác nhau của cuộc sống.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng