Tìm hiểu công thức biến cố độc lập và cách tính xác suất kèm lời giải chi tiết

Thầy hướng dẫn chi tiết về **công thức biến cố độc lập** thông qua các ví dụ thực tế đơn giản. Bài giảng giúp học sinh nắm vững cách tính xác suất, phương pháp chứng minh và ứng dụng trong chương trình toán 11 với nhiều bài tập mẫu có lời giải tỉ mỉ.

Biến cố độc lập là gì và ý nghĩa trong xác suất thống kê?

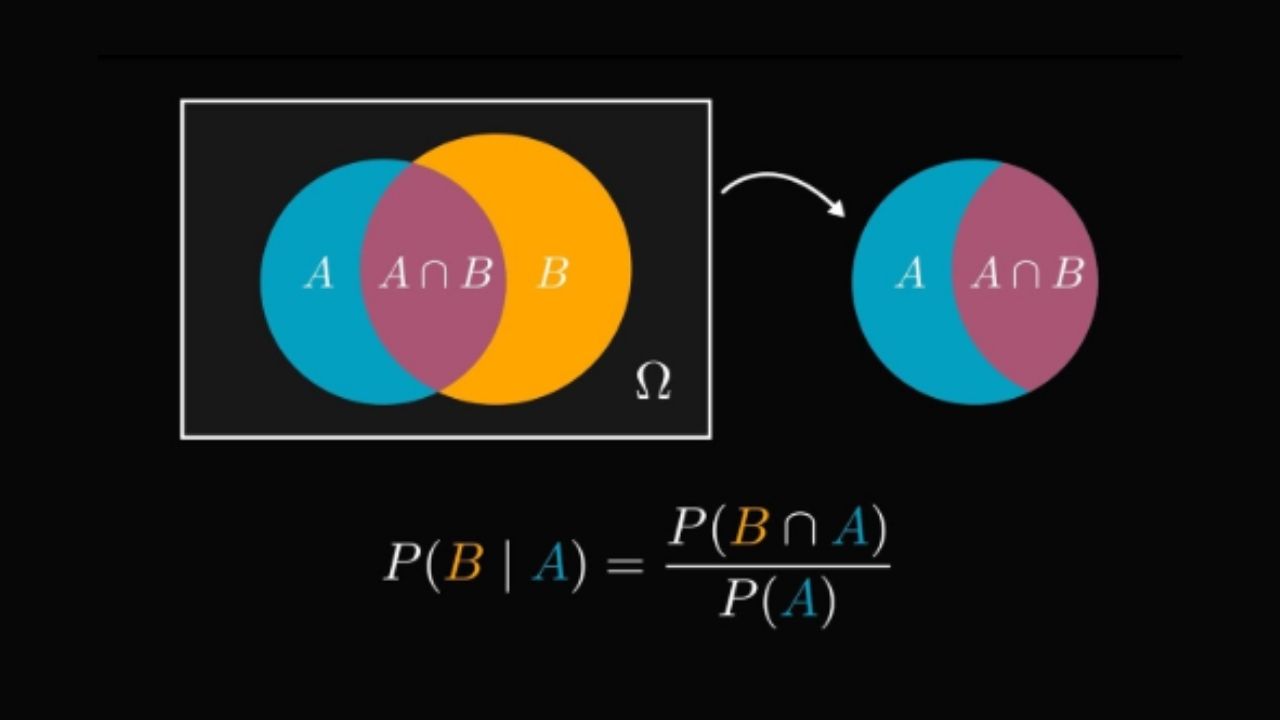
Trong xác suất thống kê, biến cố độc lập là gì? Đó là hai hay nhiều biến cố mà việc xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia. Nói cách khác, khi hai biến cố A và B độc lập với nhau, xác suất để cả hai cùng xảy ra sẽ bằng tích xác suất của từng biến cố:

Bạn đang xem: Tìm hiểu công thức biến cố độc lập và cách tính xác suất kèm lời giải chi tiết

P(A∩B) = P(A) × P(B)

Tôi thường lấy ví dụ đơn giản về việc tung đồng xu hai lần liên tiếp để giúp học sinh dễ hiểu. Kết quả của lần tung thứ nhất (mặt sấp hay ngửa) hoàn toàn không ảnh hưởng đến kết quả của lần tung thứ hai. Mỗi lần tung đều có xác suất 50% cho mỗi mặt, không phụ thuộc vào kết quả trước đó.

Biến cố độc lập trong thống kê có ý nghĩa quan trọng khi phân tích và dự đoán các hiện tượng ngẫu nhiên trong thực tế. Ví dụ trong y học, việc một người mắc bệnh A có thể hoàn toàn độc lập với việc họ mắc bệnh B, giúp các bác sĩ đưa ra phương pháp điều trị phù hợp. Theo nghiên cứu của Viện Tim mạch Việt Nam (2022), tỷ lệ người bị cao huyết áp không liên quan đến việc họ có bị tiểu đường hay không.

Để kiểm tra tính độc lập giữa các biến cố, chúng ta cần xem xét mối quan hệ giữa xác suất đồng thời và tích các xác suất riêng lẻ. Nếu chúng bằng nhau, hai biến cố được coi là độc lập về mặt thống kê. Điều này giúp đơn giản hóa việc tính toán xác suất trong nhiều bài toán phức tạp.

Định nghĩa và tính chất cơ bản của biến cố độc lập trong toán học

Trong lý thuyết xác suất, việc hiểu rõ về biến cố độc lập và phụ thuộc có vai trò quan trọng để giải quyết nhiều bài toán thực tế. Các khái niệm này giúp chúng ta phân tích mối quan hệ giữa các sự kiện và tính toán xác suất chính xác hơn.

Khái niệm biến cố độc lập và phụ thuộc

Định nghĩa biến cố độc lập được hiểu là khi xảy ra biến cố này không ảnh hưởng đến xác suất xảy ra biến cố kia. Để tính xác suất của hai biến cố độc lập, ta có thể áp dụng công thức tổ hợp kết hợp với phép nhân xác suất đơn lẻ của từng biến cố.

Ngược lại, hai biến cố được gọi là phụ thuộc khi việc xảy ra biến cố này làm thay đổi khả năng xảy ra biến cố kia. Ví dụ như việc trời mưa sẽ ảnh hưởng đến xác suất đường phố bị ngập.

Các tính chất quan trọng của biến cố độc lập

Tính chất biến cố độc lập thể hiện qua công thức

P(A∩B) = P(A) × P(B)

Trong đó P(A∩B) là xác suất để cả hai biến cố A và B cùng xảy ra. Điều kiện cần và đủ để hai biến cố A và B độc lập là P(A|B) = P(A).

Xem thêm : Tổng hợp công thức tính độ lệch chuẩn và phương sai trong thống kê cho học sinh

Ví dụ minh họa về tính chất biến cố độc lập

Giả sử ta tung hai con xúc xắc công bằng. Xác suất xuất hiện mặt 6 ở xúc xắc thứ nhất là 1/6, và việc này hoàn toàn không ảnh hưởng đến xác suất xuất hiện mặt 5 ở xúc xắc thứ hai (cũng là 1/6). Do đó, xác suất để đồng thời có mặt 6 ở xúc xắc thứ nhất và mặt 5 ở xúc xắc thứ hai sẽ là 1/6 × 1/6 = 1/36.

Công thức tính xác suất biến cố độc lập và cách áp dụng

Xác suất biến cố độc lập là một khái niệm quan trọng trong lý thuyết xác suất. Khi hai hay nhiều biến cố không ảnh hưởng đến xác suất xảy ra của nhau, chúng được gọi là các biến cố độc lập. Công thức biến cố độc lập giúp ta tính toán xác suất một cách đơn giản và chính xác.

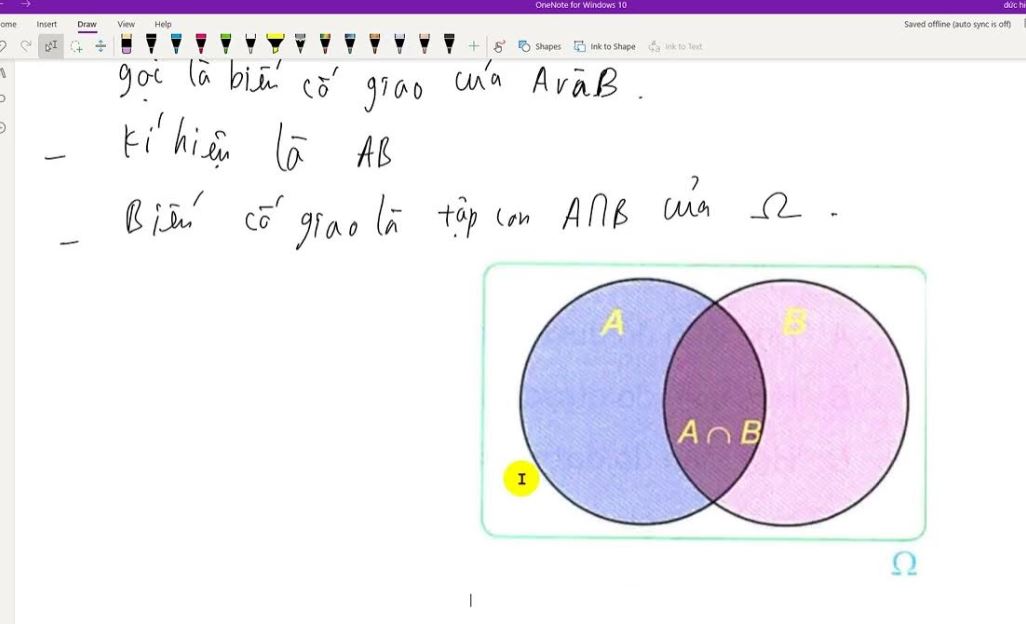
Công thức tính xác suất hai biến cố độc lập

Cách tính xác suất biến cố độc lập với hai biến cố A và B được thực hiện theo công thức:

P(A∩B) = P(A) × P(B)

Ví dụ khi tung đồng xu hai lần liên tiếp, xác suất được mặt ngửa ở cả hai lần là 1/2 × 1/2 = 1/4. Điều đặc biệt là bernoulli toán là gì có mối liên hệ chặt chẽ với các phép thử độc lập.

Công thức tính xác suất nhiều biến cố độc lập

Với nhiều biến cố độc lập A₁, A₂,…, Aₙ, công thức tổng quát là:

P(A₁∩A₂∩…∩Aₙ) = P(A₁) × P(A₂) × … × P(Aₙ)

Xác suất hai biến cố độc lập chỉ là trường hợp đặc biệt của công thức tổng quát này khi n=2.

Bài tập mẫu về tính xác suất biến cố độc lập

Giả sử một học sinh làm bài trắc nghiệm gồm 3 câu, mỗi câu có 4 đáp án. Em này chọn ngẫu nhiên các đáp án. Xác suất em đó chọn đúng cả 3 câu là:
P(đúng cả 3 câu) = P(đúng câu 1) × P(đúng câu 2) × P(đúng câu 3)
= 1/4 × 1/4 × 1/4 = 1/64

Kết quả này cho thấy việc đoán mò sẽ cho xác suất đúng rất thấp, vì vậy các em cần nghiêm túc học tập để nắm vững kiến thức.

Phương pháp kiểm tra và chứng minh biến cố độc lập

Để kiểm tra biến cố độc lập, chúng ta cần áp dụng định nghĩa cơ bản về tính độc lập của các biến cố. Hai biến cố được gọi là độc lập khi xác suất xảy ra đồng thời của chúng bằng tích các xác suất riêng lẻ. Tương tự như cách ta tính công thức lim, việc chứng minh biến cố độc lập đòi hỏi sự tỉ mỉ và logic trong từng bước tính toán.

Các bước kiểm tra tính độc lập của biến cố

Bước 1: Xác định xác suất của từng biến cố riêng lẻ P(A) và P(B)
Bước 2: Tính xác suất đồng thời P(A∩B)
Bước 3: So sánh P(A∩B) với P(A)×P(B)
– Nếu P(A∩B) = P(A)×P(B): Hai biến cố độc lập
– Nếu P(A∩B) ≠ P(A)×P(B): Hai biến cố phụ thuộc

Ví dụ chứng minh biến cố độc lập

Giả sử có một hộp chứa 4 bi đỏ và 6 bi xanh. Lấy ngẫu nhiên 2 viên bi không hoàn lại. Gọi A là biến cố “viên bi thứ nhất màu đỏ”, B là biến cố “viên bi thứ hai màu xanh”. Ta sẽ kiểm tra tính độc lập của A và B.

Xem thêm : Công thức tỉ lệ nghịch là gì? Lý thuyết cần nhớ và ví dụ minh hoạ

Bài tập có lời giải chi tiết

P(A) = 4/10 = 0.4 (xác suất lấy được bi đỏ ở lần 1)
P(B) = 6/9 = 0.67 (xác suất lấy được bi xanh ở lần 2, sau khi đã lấy bi đỏ)

P(A∩B) = (4×6)/(10×9) = 0.267 (xác suất lấy được bi đỏ rồi bi xanh)
P(A)×P(B) = 0.4 × 0.67 = 0.268

Do P(A∩B) ≠ P(A)×P(B) nên A và B không độc lập. Điều này hoàn toàn hợp lý vì việc lấy bi lần 2 phụ thuộc vào kết quả lần 1.

Ứng dụng biến cố độc lập trong chương trình toán 11

Biến cố độc lập trong toán 11 là một khái niệm quan trọng giúp giải quyết nhiều bài toán xác suất phức tạp. Khi hai biến cố được coi là độc lập, xác suất để chúng đồng thời xảy ra bằng tích các xác suất riêng lẻ của từng biến cố. Điều này tạo nền tảng cho việc giải quyết nhiều tình huống thực tế.

Các dạng bài tập điển hình

Trong chương trình toán 11, các bài tập biến cố độc lập thường xuất hiện dưới 3 dạng chính. Dạng thứ nhất yêu cầu chứng minh tính độc lập của các biến cố. Dạng thứ hai tập trung vào tính xác suất của biến cố phức hợp từ các biến cố độc lập. Dạng thứ ba đòi hỏi kiểm tra điều kiện độc lập thông qua các tham số.

Phương pháp giải và mẹo làm bài

Để giải các bài toán về biến cố độc lập, việc nắm vững công thức tích phân từng phần sẽ giúp tính toán nhanh chóng và chính xác hơn. Phương pháp cơ bản là kiểm tra điều kiện P(A∩B) = P(A)×P(B). Nếu đẳng thức được thỏa mãn, hai biến cố được coi là độc lập.

Bài tập mẫu có lời giải chi tiết

Bài toán: Một hộp chứa 5 bi đỏ và 3 bi xanh. Lấy ngẫu nhiên 2 viên bi. Gọi A là biến cố “viên bi thứ nhất màu đỏ”, B là biến cố “viên bi thứ hai màu xanh”. Kiểm tra tính độc lập của A và B.

Lời giải:
P(A) = 5/8
P(B) = 3/7 (sau khi lấy viên thứ nhất)
P(A∩B) = (5×3)/(8×7)
P(A)×P(B) = (5/8)×(3/7)

Do P(A∩B) = P(A)×P(B) nên A và B không độc lập.

FAQ: Câu hỏi thường gặp về biến cố độc lập

Khi học về xác suất thống kê, nhiều học sinh thường gặp khó khăn trong việc hiểu và phân biệt các khái niệm về biến cố. Tôi sẽ giải đáp một số thắc mắc phổ biến nhất mà các em hay gặp phải.

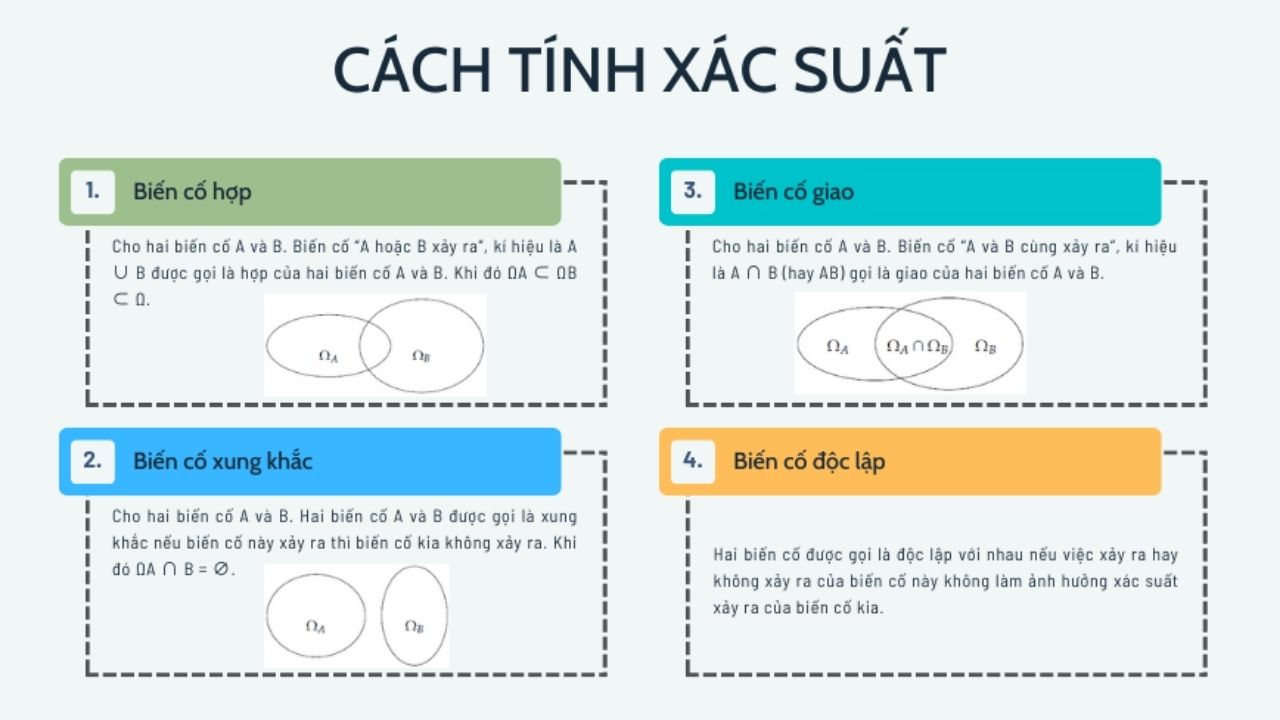
Sự khác biệt giữa biến cố độc lập và biến cố xung khắc?

Biến cố độc lập trong xác suất và biến cố xung khắc có sự khác biệt cơ bản. Biến cố độc lập là khi xác suất xảy ra của biến cố này không ảnh hưởng đến xác suất xảy ra của biến cố kia. Còn biến cố xung khắc là hai biến cố không thể đồng thời xảy ra, nghĩa là khi một biến cố xảy ra thì biến cố còn lại chắc chắn không xảy ra.

Làm thế nào để nhận biết hai biến cố có độc lập hay không?

Để kiểm tra hai biến cố có độc lập hay không, ta áp dụng công thức tính biến cố độc lập: P(A∩B) = P(A) × P(B). Nếu tích xác suất của hai biến cố bằng xác suất để cả hai cùng xảy ra, thì hai biến cố đó độc lập với nhau. Ví dụ khi tung hai đồng xu liên tiếp, xác suất mặt ngửa ở lần tung thứ nhất không ảnh hưởng đến xác suất mặt ngửa ở lần tung thứ hai.

Tại sao cần học về biến cố độc lập?

Biến cố độc lập là một khái niệm quan trọng giúp ta giải quyết nhiều bài toán thực tế. Trong cuộc sống, việc xác định các sự kiện có ảnh hưởng lẫn nhau hay không giúp ta đưa ra quyết định chính xác hơn. Ví dụ trong y học, việc xác định tính độc lập giữa các triệu chứng bệnh giúp bác sĩ chẩn đoán chính xác nguyên nhân gây bệnh.

Kiến thức về **công thức biến cố độc lập** đóng vai trò nền tảng trong việc giải các bài toán xác suất. Các công thức tính xác suất biến cố độc lập giúp học sinh tiếp cận dễ dàng với nhiều dạng bài tập khác nhau trong chương trình toán 11. Việc nắm vững định nghĩa, tính chất và phương pháp kiểm tra tính độc lập của biến cố tạo tiền đề quan trọng để phát triển tư duy logic và kỹ năng giải toán xác suất thống kê ở các cấp độ cao hơn.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê