Trang chủ » Công thức tính diện tích tam giác thường, cân, đều, vuông

Công thức tính diện tích tam giác thường, cân, đều, vuông

Tổng hợp đầy đủ công thức tính diện tích tam giác đã được chứng minh và sử dụng thường xuyên nhất hiện nay. Linh hoạt áp dụng công thức tính diện tích tam giác thường, diện tích tam giác cân, tam giác đều, tam giác vuông,….để nhanh chóng tìm ra đáp án.

Có thể bạn quan tâm

Table of Contents

Diện tích tam giác là gì?

Diện tích tam giác là đại lượng thể hiện phạm vi của hình tam giác trong mặt phẳng. Diện tích có thể được xác định bằng đơn vị cm2, m2, dm2,…

Bạn đang xem: Công thức tính diện tích tam giác thường, cân, đều, vuông

Công thức diện tích tam giác thường

Tham khảo các công thức diện tích tam giác dưới đây:

1/ Công thức tính diện tích tam giác cơ bản

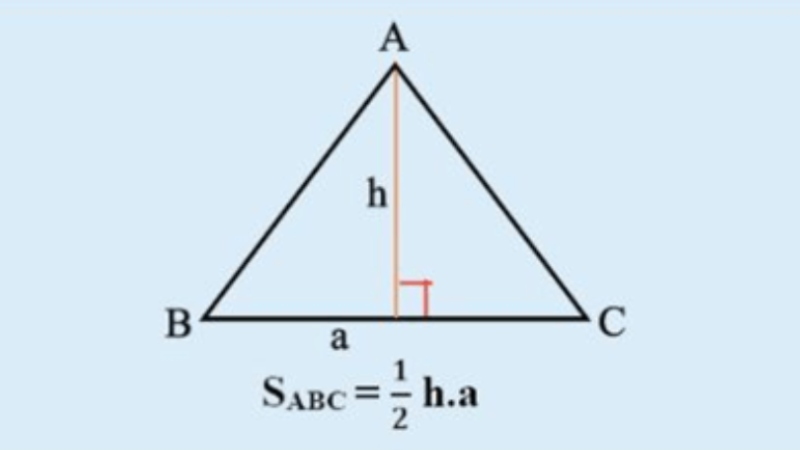
Cho một tam giác bất kỳ có chiều cao là h, độ dài cạnh chân đường cao là a. Công thức tổng quát tính diện tích tam giác như sau:

S = ½ah

Ví dụ: Tính diện tích tam giác ABC. Cho biết, AH là đường cao được kẻ từ đỉnh A có độ dài là 5cm, BC có chiều dài là 10cm.

Lời giải:

Diện tích tam giác ABC là: S=½ah = ½*5*10 = 25 cm2

2/ Các công thức tính diện tích tam giác dựa vào số đo góc

Khi biết trước số đo một góc, bạn có thể sử dụng công thức sau để xác định diện tích một cách nhanh chóng hơn:

Xem thêm : Chi tiết công thức tính chiều cao hình thang và phương pháp xác định chuẩn xác nhất

S= ½abSinC = ½acSinB = ½bcSinA

3/ Công thức tính s tam giác dựa vào chu vi

Gọi p là nửa chu vi của tam giác, ta có công thức tình diện tích như sau:

S = p(p-a)(p-b)(p-c)

4/ Công thức tính diện tích tam giác trong không gian

Công thức tính diện tích tam giác trong không gian:

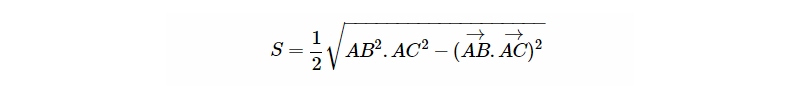
công thức diện tích tam giác

Công thức tính diện tích hình tam giác đặc biệt

Với một số loại tam giác đặc biệt, công thức xác định diện tích thường chi tiết và cụ thể hơn. Các công thức dưới đây đều được thiết lập dựa trên tính chất cơ bản của từng loại tam giác.

1/ Công thức tính diện tích tam giác đều

Tam giác đều là tam giác có 3 cạnh và 3 góc bằng nhau. Mỗi góc trong tam giác đều có số đo là 60 độ.

Diện tích tam giác đều được tính như sau:

S =a2 34

2/ Công thức tính diện tích tam giác cân

Xem thêm : Các công thức tính đường kính hình tròn và mẹo làm bài tập đơn giản

Tam giác cân có đặc trưng là có hai cạnh bằng nhau và 2 góc đáy bằng nhau.

Diện tích tam giác cân như sau:

S = 1/2ah

Trong đó:

a là chiều dài cạnh đáy
h là độ dài đường cao từ đỉnh đối diện

3/ Công thức tính diện tích tam giác vuông

Cho tam giác ABC, vuông tại A, chiều dài hai cạnh góc vuông lần lượt là a và b. Công thức tính diện tích tam giác là:

S= 1/2ab

4/ Công thức tính diện tích tam giác vuông cân

Tam giác cân vuông không chỉ có một góc vuông mà còn có chiều dài hai cạnh góc vuông bằng nhau.

S = 1/2a2

Kết luận

Tham khảo công thức tính diện tích tam giác được tổng hợp chuẩn xác để ứng dụng trong quá trình học tập. Hy vọng những thông tin bổ ích này sẽ giúp bạn đạt được kết quả cao trong kỳ thi sắp tới.

Nguồn: https://congthuctoan.com
Danh mục: Hình học phẳng