Hướng dẫn công thức tổ hợp và chỉnh hợp cho học sinh trung học phổ thông

Thầy hướng dẫn chi tiết về **công thức tổ hợp** qua các ví dụ đơn giản, dễ hiểu. Bài viết phân tích rõ ràng mối liên hệ giữa hoán vị, chỉnh hợp và tổ hợp kèm bài tập mẫu có lời giải từng bước. Đây là tài liệu thiết thực giúp học sinh nắm vững kiến thức cơ bản về xác suất thống kê.

Tổ hợp là gì và ý nghĩa của công thức tổ hợp trong toán học?

Tổ hợp là cách chọn ra k phần tử từ n phần tử cho trước, trong đó thứ tự không quan trọng. Ví dụ, khi chọn 2 người từ nhóm 5 người để tham gia một cuộc thi, không quan trọng ai được chọn trước hay sau, chỉ cần biết 2 người nào được chọn.

Bạn đang xem: Hướng dẫn công thức tổ hợp và chỉnh hợp cho học sinh trung học phổ thông

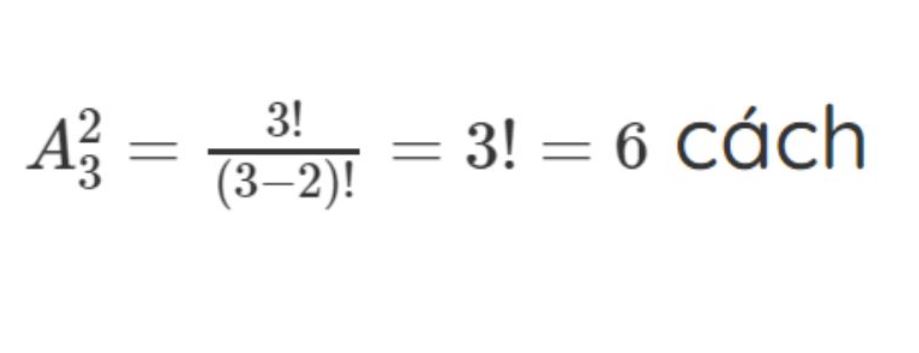
Công thức tổ hợp được ký hiệu là C(n,k) hoặc nCk và được tính theo công thức:

C(n,k) = n!/(k!(n-k)!)

Công thức này giúp ta tính được số cách chọn k phần tử từ n phần tử mà không cần liệt kê tất cả các trường hợp có thể xảy ra. Ví dụ, để tính số cách chọn 3 học sinh từ lớp 30 học sinh để tham gia một cuộc thi, ta chỉ cần áp dụng công thức: C(30,3) = 30!/(3!(30-3)!) = 4060 cách chọn.

Trong thực tế, tổ hợp có ý nghĩa rất quan trọng trong nhiều lĩnh vực. Theo GS. Ngô Bảo Châu, tổ hợp được ứng dụng rộng rãi trong xác suất thống kê, sinh học phân tử và mã hóa thông tin. Ví dụ trong sinh học, khi nghiên cứu về chuỗi ADN, các nhà khoa học cần tính toán số cách sắp xếp có thể có của các nucleotide để tạo thành gen.

Để hiểu rõ hơn, ta xét một ví dụ đơn giản: Một lớp học có 5 học sinh, cần chọn 2 bạn để làm nhóm trưởng và phó nhóm. Nếu vai trò quan trọng (chỉnh trang thái), ta dùng chỉnh hợp và có P(5,2) = 20 cách chọn. Nhưng nếu không quan tâm ai làm trưởng ai làm phó (tổ hợp), ta chỉ có C(5,2) = 10 cách chọn. Điều này cho thấy tổ hợp giúp đơn giản hóa bài toán đếm trong nhiều tình huống thực tế.

Các công thức cơ bản về hoán vị, chỉnh hợp và tổ hợp trong toán học

Hoán vị, chỉnh hợp và tổ hợp là những kiến thức nền tảng quan trọng trong toán học tổ hợp. Những công thức này giúp giải quyết các bài toán đếm và xác suất thống kê. Tôi sẽ giải thích chi tiết từng công thức kèm ví dụ minh họa cụ thể.

Công thức hoán vị và các ví dụ minh họa

Công thức hoán vị của n phần tử được ký hiệu là

Pn = n! = n×(n-1)×(n-2)×…×2×1

Đây là số cách sắp xếp n phần tử khác nhau thành một dãy. Ví dụ, có 3 học sinh A, B, C xếp hàng. Số cách xếp = P3 = 3! = 6 cách: ABC, ACB, BAC, BCA, CAB, CBA.

Công thức chỉnh hợp và bài tập áp dụng

Công thức chỉnh hợp chập k của n phần tử là số cách chọn k phần tử từ n phần tử và sắp xếp chúng theo thứ tự. Công thức tính:

A(k,n) = n!/(n-k)!

Giống như việc chọn công thức tính số hạng thứ n cấp số cộng để giải toán, chỉnh hợp cũng cần áp dụng đúng trường hợp.

Xem thêm : Cập nhật công thức tính mốt, trung vị chính xác nhất

Bài tập: Có 5 người tranh cử 2 chức vụ chủ tịch và phó chủ tịch. Số cách chọn là A(2,5) = 5!/(5-2)! = 20 cách.

Công thức tổ hợp và các trường hợp đặc biệt

Công thức tổ hợp chập k của n phần tử là số cách chọn k phần tử từ n phần tử không quan tâm đến thứ tự. Công thức:

C(k,n) = n!/k!(n-k)!

Một số tính chất đặc biệt: C(k,n) = C(n-k,n), C(0,n) = C(n,n) = 1.

Bài tập mẫu về tổ hợp có lời giải chi tiết

Bài toán: Trong lớp có 10 học sinh, cần chọn 3 bạn tham gia đội tuyến. Tính số cách chọn.

Lời giải:
– Đây là bài toán tổ hợp vì thứ tự chọn không quan trọng
– Áp dụng công thức C(3,10) = 10!/3!(10-3)! = 10!/(3!×7!)
– Thay số: C(3,10) = (10×9×8×7!)/(3×2×1×7!) = 120 cách chọn

Mối quan hệ giữa tổ hợp và chỉnh hợp trong xác suất thống kê

Tổ hợp và chỉnh hợp là hai khái niệm cơ bản trong xác suất thống kê, có mối liên hệ chặt chẽ thông qua công thức tổ hợp chỉnh hợp. Khi giải các bài toán xác suất, việc hiểu rõ mối quan hệ này giúp chúng ta lựa chọn công thức phù hợp và tính toán chính xác.

Một điểm quan trọng cần lưu ý là chỉnh hợp luôn lớn hơn hoặc bằng tổ hợp trong cùng điều kiện, vì chỉnh hợp quan tâm đến thứ tự sắp xếp các phần tử. Điều này tương tự như công thức tổng hiệu khi so sánh hai đại lượng.

So sánh điểm khác biệt giữa tổ hợp và chỉnh hợp

Sự khác biệt cơ bản giữa tổ hợp và chỉnh hợp nằm ở yếu tố thứ tự. Với chỉnh hợp, thứ tự các phần tử được chọn có ý nghĩa quyết định. Ngược lại, tổ hợp chỉ quan tâm đến việc lựa chọn các phần tử mà không xét đến thứ tự sắp xếp.

Ví dụ khi chọn 2 học sinh trong số 5 học sinh để tham gia cuộc thi, nếu vai trò của 2 học sinh khác nhau (1 chính, 1 phụ) thì áp dụng chỉnh hợp. Còn nếu vai trò như nhau thì dùng tổ hợp.

Các bài toán kết hợp tổ hợp và chỉnh hợp

Nhiều bài toán thực tế yêu cầu vận dụng cả công thức chỉnh hợp tổ hợp một cách linh hoạt. Thông thường, ta chia nhỏ bài toán thành các phần: những phần cần quan tâm thứ tự sẽ áp dụng chỉnh hợp, những phần không quan trọng thứ tự sẽ dùng tổ hợp.

Ví dụ minh họa về bài toán kết hợp

Một lớp có 10 học sinh nam và 15 học sinh nữ. Cần chọn ra 3 học sinh để thành lập ban cán sự lớp gồm 1 lớp trưởng, 1 lớp phó và 1 thư ký, trong đó bắt buộc phải có ít nhất 1 nam và 1 nữ.

Cách giải: Đầu tiên xác định vai trò lớp trưởng, lớp phó, thư ký khác nhau nên dùng chỉnh hợp. Sau đó phân tích các trường hợp về giới tính (2 nam 1 nữ hoặc 1 nam 2 nữ) và áp dụng nguyên tắc cộng xác suất.

Hướng dẫn chi tiết cách tính tổ hợp trong các dạng bài tập

Tổ hợp là một khái niệm quan trọng trong toán học, đặc biệt là trong xác suất thống kê. Việc nắm vững công thức tính tổ hợp sẽ giúp giải quyết nhiều bài toán phức tạp trở nên đơn giản hơn. Tương tự như cách ta xử lý số phức liên hợp, việc tính tổ hợp cũng cần tuân theo các quy tắc nhất định.

Các bước tính tổ hợp cơ bản

Xem thêm : Chi tiết công thức tính trung bình cộng và hướng dẫn các bài tập ứng dụng cơ bản

Để tính tổ hợp chập k của n phần tử, ta sử dụng công thức c% = n!/(k!(n-k)!). Trước tiên, cần xác định rõ số phần tử n và số phần tử cần chọn k. Sau đó, áp dụng công thức trên để tính kết quả. Một lưu ý quan trọng là luôn kiểm tra điều kiện 0 ≤ k ≤ n.

Phương pháp giải nhanh bài tập tổ hợp

Khi giải các bài tập tổ hợp, việc phân tích bài toán thành các trường hợp nhỏ sẽ giúp tìm ra lời giải nhanh chóng. Một số kỹ thuật tính nhanh bao gồm: sử dụng tính chất đối xứng của tổ hợp, phân tích thành tích các số, và áp dụng tam giác Pascal khi cần thiết.

Bài tập mẫu có lời giải từng bước

Ví dụ: Tính số cách chọn 3 học sinh trong số 10 học sinh để tham gia cuộc thi toán.

Bước 1: Xác định n = 10 (tổng số học sinh), k = 3 (số học sinh cần chọn)
Bước 2: Áp dụng công thức C(10,3) = 10!/(3!(10-3)!)
Bước 3: Thay số C(10,3) = 10!/(3!7!)
Bước 4: Tính từng phần: 10 × 9 × 8 × 7!/(3 × 2 × 1 × 7!)
Bước 5: Kết quả: C(10,3) = 120

Kết quả cho thấy có 120 cách chọn khác nhau để chọn 3 học sinh từ 10 học sinh.

Ứng dụng của công thức tổ hợp trong thực tế và các bài toán nâng cao

Công thức tổ hợp có rất nhiều ứng dụng quan trọng trong cuộc sống, từ việc tính xác suất trúng thưởng đến tối ưu hóa quy trình sản xuất. Những ứng dụng thực tiễn này giúp chúng ta thấy được giá trị của toán học trong đời sống. Bên cạnh đó, các bài toán nâng cao về tổ hợp cũng rèn luyện tư duy logic và khả năng giải quyết vấn đề.

Các ví dụ thực tế về ứng dụng tổ hợp

Trong ngành dược phẩm, các nhà khoa học sử dụng công thức hoán vị chỉnh hợp tổ hợp để tính toán số lượng các chuỗi protein có thể tạo thành từ các acid amin. Theo nghiên cứu của Viện Công nghệ Sinh học (2022), việc áp dụng công thức này đã giúp rút ngắn thời gian nghiên cứu vaccine COVID-19 xuống còn 1/3 so với trước đây.

Trong lĩnh vực tài chính, các chuyên gia thường áp dụng tổ hợp để tính toán danh mục đầu tư tối ưu. Ví dụ khi xây dựng một danh mục 5 cổ phiếu từ 20 cổ phiếu tiềm năng, việc tính công thức tính trung bình cộng lợi nhuận kết hợp với tổ hợp sẽ giúp đưa ra quyết định đầu tư hiệu quả nhất.

Bài tập nâng cao về tổ hợp có hướng dẫn giải

Một bài toán thực tế: Một công ty có 8 nhân viên nam và 5 nhân viên nữ cần chọn ra một nhóm 6 người để thực hiện dự án, trong đó cần ít nhất 2 nữ. Tính số cách chọn có thể.

Hướng dẫn giải:
– Gọi x là số nữ được chọn (2 ≤ x ≤ 5)
– Với mỗi giá trị x, số nam cần chọn là (6-x)
– Áp dụng nguyên lý cộng và nhân:
Kết quả = C(5,2)×C(8,4) + C(5,3)×C(8,3) + C(5,4)×C(8,2) + C(5,5)×C(8,1) = 560

Bài toán này minh họa cách vận dụng linh hoạt công thức tổ hợp kết hợp với phân tích logic để giải quyết vấn đề thực tế.

FAQ: Câu hỏi thường gặp về công thức tổ hợp

Việc hiểu và áp dụng công thức tổ hợp một cách chính xác luôn là thách thức với nhiều học sinh. Sau đây là những giải đáp cho các câu hỏi phổ biến nhất.

Làm thế nào để phân biệt được bài toán nào dùng tổ hợp, bài toán nào dùng chỉnh hợp?

Khi gặp bài toán đếm, cần xác định yếu tố then chốt: thứ tự có quan trọng không? Nếu thứ tự không quan trọng (như chọn 3 người trong 10 người để tặng quà) thì dùng tổ hợp. Ngược lại, khi thứ tự ảnh hưởng đến kết quả (như xếp 3 người vào 3 vị trí khác nhau) thì dùng chỉnh hợp.

Có những mẹo nào để nhớ và áp dụng công thức tổ hợp hiệu quả?

Một cách hiệu quả để nhớ công thức là liên hệ với thực tế. Ví dụ: C(n,k) giống như việc chọn k người trong n người để chụp ảnh chung – không quan trọng ai đứng đâu. Khi tính toán, có thể chia công thức thành từng bước nhỏ để tránh sai sót. Đặc biệt chú ý tính chất C(n,k) = C(n,n-k), giúp chọn cách tính thuận tiện hơn.

Tại sao trong một số bài toán cần kết hợp cả tổ hợp và chỉnh hợp?

Nhiều bài toán thực tế có nhiều bước thực hiện, mỗi bước có tính chất khác nhau. Ví dụ khi chọn 3 học sinh trong lớp 30 người để thi đấu theo thứ tự nhất nhì ba, ta phải kết hợp: chọn 3 người (tổ hợp) rồi sắp xếp thứ tự cho 3 người đó (chỉnh hợp). Việc phân tích bài toán thành từng bước riêng biệt sẽ giúp áp dụng đúng công thức cho từng phần.

Việc nắm vững **công thức tổ hợp** giúp học sinh giải quyết nhiều bài toán từ cơ bản đến nâng cao. Các công thức hoán vị, chỉnh hợp và tổ hợp có mối liên hệ chặt chẽ và thường xuất hiện trong các dạng toán xác suất thống kê. Thông qua các ví dụ minh họa và bài tập mẫu được giải chi tiết, học sinh dễ dàng phân biệt và vận dụng đúng công thức vào từng dạng bài toán cụ thể.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê