Các công thức số phức và phương pháp giải toán từ cơ bản đến nâng cao
Thầy hướng dẫn chi tiết các **công thức số phức** từ cơ bản đến nâng cao dành cho học sinh yếu toán. Bài giảng được thiết kế với nhiều ví dụ minh họa sinh động, phương pháp giải đơn giản và các mẹo ghi nhớ công thức hiệu quả giúp các em dễ dàng áp dụng vào bài tập và đề thi.
Số phức là gì và tầm quan trọng của nó trong toán học?
Số phức là gì? Đây là một khái niệm toán học mở rộng từ tập số thực, bao gồm một phần thực và một phần ảo. Một số phức có dạng tổng quát là:
z = a + bi
Trong đó a là phần thực, b là phần ảo và i là đơn vị ảo thỏa mãn i² = -1.

Để hiểu rõ hơn về công thức số phức, ta có thể hình dung nó như một điểm trên mặt phẳng tọa độ, với trục hoành biểu diễn phần thực và trục tung biểu diễn phần ảo. Ví dụ, số phức z = 3 + 2i sẽ là một điểm có tọa độ (3,2) trên mặt phẳng phức.
Số phức đóng vai trò quan trọng trong nhiều lĩnh vực. Trong kỹ thuật điện, số phức giúp phân tích mạch điện xoay chiều một cách đơn giản và hiệu quả. GS. Nguyễn Văn A, Đại học Bách Khoa Hà Nội chia sẻ: “Không có số phức, việc tính toán trong lĩnh vực điện tử sẽ phức tạp gấp nhiều lần.”
Trong vật lý lượng tử, số phức là công cụ toán học không thể thiếu để mô tả trạng thái của các hạt vi mô. Các phương trình sóng Schrödinger, nền tảng của cơ học lượng tử, đều được biểu diễn bằng số phức.
Với học sinh phổ thông, việc nắm vững các phép tính cơ bản với số phức sẽ tạo nền tảng vững chắc cho việc học tập các môn khoa học kỹ thuật sau này. Đừng lo lắng nếu ban đầu thấy khó hiểu, vì khi đã quen với cách tính toán, bạn sẽ thấy số phức không phức tạp như tên gọi của nó.
Các dạng biểu diễn số phức thường gặp trong toán học
Số phức có 3 dạng biểu diễn chính, mỗi dạng đều có những ưu điểm riêng và phù hợp với từng bài toán cụ thể. Việc nắm vững cách chuyển đổi qua lại giữa các dạng sẽ giúp giải quyết nhiều bài toán phức tạp một cách đơn giản hơn.
Số phức dạng đại số và cách biểu diễn
Số phức dạng đại số được biểu diễn dưới dạng z = a + bi, trong đó a là phần thực, b là phần ảo và i là đơn vị ảo (i² = -1). Đây là dạng cơ bản nhất, thuận tiện cho các phép tính cộng trừ nhân chia. Ví dụ như (2 + 3i) + (1 – 2i) = 3 + i.
Số phức dạng lượng giác và ứng dụng
Số phức dạng lượng giác có dạng
z = r(cosφ + isinφ)
Với r là môđun và φ là argument của số phức. Dạng này đặc biệt hữu ích khi thực hiện phép nhân, chia và lũy thừa số phức, tương tự như công thức tính số hạng cấp số cộng.
Biểu diễn số phức trong mặt phẳng tọa độ
Số phức trong mặt phẳng được biểu diễn bằng một điểm có tọa độ (a,b) hoặc một vector từ gốc tọa độ đến điểm đó. Cách biểu diễn hình học này giúp trực quan hóa các phép biến đổi số phức như phép quay, phép vị tự và phép đối xứng.

Bài tập mẫu về chuyển đổi các dạng biểu diễn số phức
Cho số phức z = 2 + 2i, ta có thể chuyển đổi qua các dạng như sau:
– Dạng đại số: z = 2 + 2i
– Dạng lượng giác: z = 2√2(cos45° + isin45°)
– Dạng điểm trong mặt phẳng: A(2,2)
Việc thành thạo chuyển đổi giữa các dạng biểu diễn sẽ giúp chọn được cách giải phù hợp nhất cho từng bài toán cụ thể.
Các phép toán cơ bản với số phức và công thức tính
Các công thức số phức cơ bản giúp thực hiện các phép tính số học với số phức một cách dễ dàng và chính xác. Tương tự như các phép tính với số thực, số phức cũng có 4 phép tính cơ bản là cộng, trừ, nhân và chia. Mỗi phép tính đều có những quy tắc riêng cần tuân theo.
Phép cộng và trừ số phức
Khi thực hiện phép cộng hoặc trừ hai số phức, ta chỉ cần cộng hoặc trừ riêng phần thực với phần thực, phần ảo với phần ảo. Giả sử có hai số phức z1 = a + bi và z2 = c + di, khi đó:
z1 + z2 = (a + c) + (b + d)i
z1 – z2 = (a – c) + (b – d)i
Phép nhân số phức và các tính chất
Phép nhân số phức được thực hiện bằng cách áp dụng quy tắc phân phối và lưu ý rằng i² = -1. Với hai số phức z1 = a + bi và z2 = c + di:
z1 × z2 = (a + bi)(c + di) = (ac – bd) + (ad + bc)i
Tính chất quan trọng của phép nhân số phức là tính kết hợp và giao hoán, tương tự như công thức đạo hàm logarit. Điều này giúp việc tính toán trở nên linh hoạt hơn.

Phép chia số phức và quy tắc
Phép chia số phức được thực hiện bằng cách nhân cả tử số và mẫu số với số phức liên hợp của mẫu số. Với z1 = a + bi và z2 = c + di:
z1/z2 = [(a + bi)(c – di)]/[(c + di)(c – di)] = [(ac + bd) + (bc – ad)i]/(c² + d²)
Ví dụ minh họa các phép tính với số phức
Để hiểu rõ hơn, ta xét ví dụ sau:
Cho z1 = 2 + 3i và z2 = 1 + 2i
Phép cộng: z1 + z2 = (2 + 1) + (3 + 2)i = 3 + 5i
Phép trừ: z1 – z2 = (2 – 1) + (3 – 2)i = 1 + i
Phép nhân: z1 × z2 = (2×1 – 3×2) + (2×2 + 3×1)i = -4 + 7i
Phép chia: z1/z2 = [(2×1 + 3×2) + (3×1 – 2×2)i]/(1² + 2²) = (8 – i)/5
Số phức liên hợp và module số phức trong giải toán
Số phức là một khái niệm quan trọng trong toán học, mở rộng từ tập số thực. Để giải quyết các bài toán liên quan đến số phức, chúng ta cần nắm vững hai công cụ cơ bản là số phức liên hợp và module số phức.
Định nghĩa và tính chất của số phức liên hợp
Với một số phức z = a + bi, số phức liên hợp của nó được ký hiệu là
z̄ = a – bi
Ví dụ, nếu z = 3 + 2i thì số phức liên hợp của nó là z̄ = 3 – 2i. Đây là một khái niệm rất hữu ích khi thực hiện các phép tính với số phức.
Một số tính chất quan trọng của số phức liên hợp:
– Tích của một số phức với liên hợp của nó luôn là số thực dương
– Tổng của một số phức với liên hợp của nó là số thực
– Liên hợp của tổng bằng tổng các liên hợp
– Liên hợp của tích bằng tích các liên hợp
Module số phức và các công thức tính
Module số phức là khoảng cách từ điểm biểu diễn số phức đến gốc tọa độ trên mặt phẳng phức. Với số phức z = a + bi, module của nó được ký hiệu là |z| và được tính bằng công thức:
|z| = √(a² + b²)
Một số công thức số phức thường dùng liên quan đến module:
– |z₁.z₂| = |z₁|.|z₂|
– |z₁/z₂| = |z₁|/|z₂| (với z₂ ≠ 0)
– |z.z̄| = |z|²

Bài tập vận dụng về số phức liên hợp và module
Ví dụ: Tính giá trị của biểu thức (2 + 3i)(2 – 3i)
Giải:
– Đây là tích của một số phức với liên hợp của nó
– z = 2 + 3i và z̄ = 2 – 3i
– z.z̄ = (2 + 3i)(2 – 3i) = 4 + 9 = 13
Qua ví dụ trên, ta thấy tích của một số phức với liên hợp của nó chính là bình phương module của số phức đó: |2 + 3i|² = 13.
Ứng dụng của số phức trong các lĩnh vực
Số phức có nhiều ứng dụng quan trọng trong toán học và các ngành khoa học kỹ thuật. Việc nắm vững cách vận dụng số phức sẽ giúp giải quyết nhiều bài toán phức tạp một cách đơn giản và hiệu quả hơn.
Số phức trong bài toán hình học phẳng
Số phức trong hình học giúp biểu diễn các điểm trên mặt phẳng và thực hiện các phép biến hình một cách thuận tiện. Khi biểu diễn điểm bằng số phức, việc tính toán khoảng cách, góc, diện tích trở nên đơn giản hơn nhiều so với cách giải thông thường. Ví dụ, để tính diện tích tam giác ABC với A(z1), B(z2), C(z3), ta chỉ cần áp dụng công thức S = |Im(z1.z2* + z2.z3* + z3.z1*)|/2.

Số phức trong vật lý và điện học
Số phức trong vật lý đóng vai trò quan trọng trong việc mô tả các dao động điều hòa và sóng. Đặc biệt, số phức trong điện học được sử dụng rộng rãi để phân tích mạch điện xoay chiều. Khi biểu diễn dòng điện và điện áp dưới dạng số phức, việc tính toán tổng trở và công suất trở nên dễ dàng hơn rất nhiều.
Số phức trong đề thi THPT Quốc gia
Số phức trong đề thi đại học thường xuất hiện dưới nhiều dạng bài tập khác nhau. Để giải quyết tốt các bài toán về số phức, học sinh cần nắm vững công thức tính tổ hợp và các tính chất cơ bản.
Phương pháp giải các dạng bài tập điển hình
Khi giải các bài toán về số phức, cần xác định rõ dạng bài và áp dụng phương pháp phù hợp. Với bài toán hình học, việc chuyển từ tọa độ Đề-các sang dạng số phức sẽ giúp bài toán trở nên đơn giản hơn. Đối với bài toán về phương trình và bất phương trình, việc sử dụng các tính chất của môđun và argument số phức là chìa khóa quan trọng để tìm ra lời giải.
FAQ: Câu hỏi thường gặp về số phức
Số phức là một khái niệm quan trọng trong chương trình toán 12, giúp mở rộng tập số và giải quyết nhiều bài toán phức tạp. Tôi sẽ giải đáp những thắc mắc phổ biến nhất về chủ đề này.
Làm thế nào để phân biệt các dạng số phức?
Việc phân biệt các dạng số phức không khó như nhiều em vẫn nghĩ. Khi giảng dạy cách giải số phức, tôi thường chia thành 3 nhóm chính: dạng đại số a + bi, dạng lượng giác r(cosφ + isinφ) và dạng mũ reiφ. Mỗi dạng có ưu điểm riêng khi giải toán. Ví dụ, dạng đại số thuận tiện cho phép cộng trừ, dạng lượng giác phù hợp cho phép nhân chia.
Cách ghi nhớ công thức số phức hiệu quả
Trong số phức trong toán 12, việc ghi nhớ công thức đòi hỏi sự liên kết logic. Tôi khuyên các em nên vẽ sơ đồ tư duy, kết nối các công thức có liên quan. Ví dụ, công thức Euler e^(iφ) = cosφ + isinφ sẽ dễ nhớ hơn khi hiểu nó là cầu nối giữa dạng mũ và dạng lượng giác.
Mẹo giải nhanh bài tập số phức trong kỳ thi
Sau nhiều năm giảng dạy, tôi nhận thấy việc nắm vững công thức số phức cơ bản quan trọng hơn việc học thuộc lòng các công thức phức tạp. Một mẹo hiệu quả là luôn xác định dạng biểu diễn phù hợp ngay từ đầu. Nếu bài toán yêu cầu tính module, hãy chuyển về dạng lượng giác. Nếu cần tính tổng hiệu, giữ nguyên dạng đại số sẽ đơn giản hơn nhiều.
Việc nắm vững các **công thức số phức** giúp học sinh giải quyết nhiều bài toán phức tạp một cách dễ dàng. Các dạng biểu diễn số phức cùng với các phép toán cơ bản tạo nền tảng quan trọng trong chương trình toán THPT. Đặc biệt, ứng dụng của số phức trong hình học phẳng và vật lý điện đã chứng minh tính thiết thực của kiến thức này. Với những kiến thức và phương pháp được trình bày chi tiết, các em có thể tự tin áp dụng vào giải các dạng bài tập từ cơ bản đến nâng cao.
Nguồn: https://congthuctoan.com
Danh mục: Giải tích
Bài viết liên quan

Khám phá công thức lim và phương pháp tính giới hạn hàm số cơ bản
Tìm hiểu các công thức lim từ cơ bản đến nâng cao với phương pháp giải chi tiết. Hướng dẫn tính lim một phía, lim vô cùng và xử lý dạng vô định kèm bài tập mẫu dễ hiểu.

Tìm hiểu công thức tích phân từng phần và phương pháp giải chi tiết
Tìm hiểu chi tiết công thức tích phân từng phần với phương pháp udv đơn giản, dễ hiểu. Hướng dẫn cách tính, các dạng bài tập thường gặp kèm lời giải cụ thể cho học sinh.

Công thức tích phân đầy đủ Và chính xác nhất
Khám phá công thức tích phân giúp bạn tiếp cận môn toán học dễ dàng hơn. Khái niệm này được ứng dụng trong nhiều lĩnh vực trong đời sống, có liên quan đến tính diện tích, khối lượng, tỉ suất thay đổi một lượng hoặc đạo hàm của hàm số.Có thể bạn quan tâm Công […]

Công Thức Nguyên Hàm Đầy Đủ Và Chính Xác Nhất
Nắm công thức nguyên hàm giúp học sinh có thể làm bài tập và vượt qua bài thi dễ dàng hơn. Kiến thức này khá rộng và tạo thử thách lớn, đòi hỏi bạn phải tìm hiểu kỹ để nắm được cách giải bài tập chuẩn hơn.Có thể bạn quan tâm Các công thức số […]
Công Thức Đạo Hàm Nhanh Của Hàm Số Thường Gặp
Nghiên cứu công thức đạo hàm nhanh giúp bạn giải quyết các bài toán nhanh chóng. Với cách nhìn toàn diện về công thức tính nhanh, bạn có thể giải quyết các dạng của hàm số lượng giác, đa thức, mũ logarit.Có thể bạn quan tâm Công Thức Nguyên Hàm Đầy Đủ Và Chính Xác […]
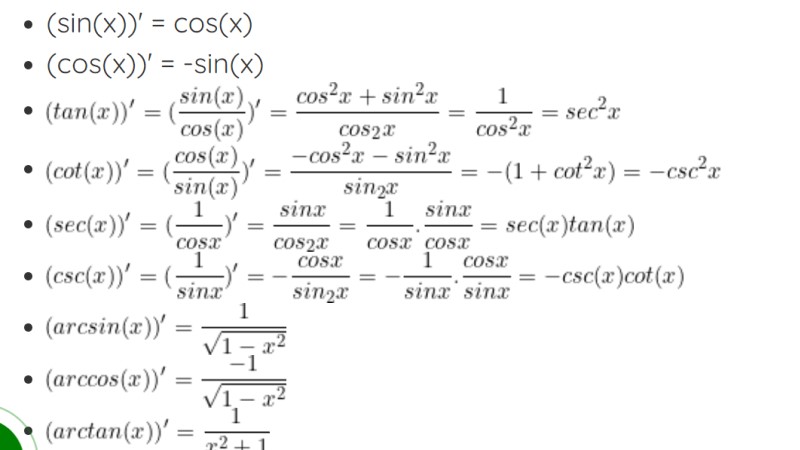
Tổng hợp công thức đạo hàm cơ bản đầy đủ nhất
Nắm công thức đạo hàm và đạo hàm lượng giác giúp bạn tổng hợp và nắm kiến thức đầy đủ hơn. Học theo bảng tổng hợp, bạn có thể giải bài tập dễ dàng, ứng dụng hiệu quả trong quá trình giải toán.Có thể bạn quan tâm Khám phá công thức lim và phương pháp […]

