Công thức số mũ và các quy tắc tính toán cơ bản trong toán học

Thầy giải thích chi tiết về **công thức số mũ** thông qua các ví dụ đơn giản và dễ hiểu. Bài viết phân tích kỹ lưỡng các quy tắc tính toán với số mũ dương, âm và số mũ 0, đồng thời làm rõ mối liên hệ giữa số mũ với căn thức, logarit và phân số trong toán học.

Số mũ là gì và vai trò của số mũ trong toán học?

Số mũ là gì – đây là phép toán viết tắt của phép nhân liên tiếp một số với chính nó nhiều lần. Ví dụ, thay vì viết 2 × 2 × 2 × 2, ta có thể viết gọn thành 2⁴. Trong đó, 2 được gọi là cơ số và 4 là số mũ.

Bạn đang xem: Công thức số mũ và các quy tắc tính toán cơ bản trong toán học

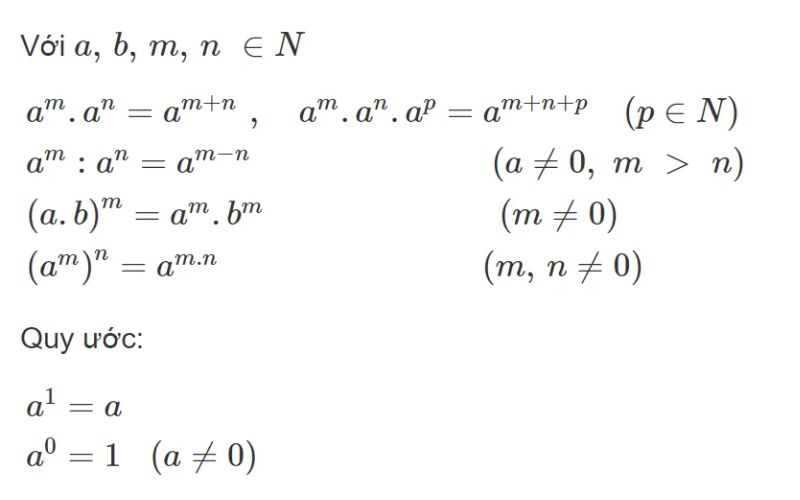
Để giúp các em dễ hiểu hơn, thầy sẽ lấy một ví dụ đơn giản: Giả sử có một cửa hàng bánh, mỗi ngày số lượng khách tăng gấp đôi. Ngày đầu có 2 khách, ngày 2 có 4 khách (2²), ngày 3 có 8 khách (2³), ngày 4 có 16 khách (2⁴). Thay vì phải nhân nhiều lần, việc sử dụng số mũ giúp ta tính toán nhanh chóng và gọn gàng hơn rất nhiều.

Số mũ trong toán học đóng vai trò vô cùng quan trọng. Nó không chỉ giúp rút gọn cách viết các phép tính phức tạp mà còn là nền tảng cho nhiều ứng dụng thực tiễn. Trong khoa học máy tính, số mũ được sử dụng để tính toán dung lượng lưu trữ (byte, kilobyte, megabyte). Trong tài chính, số mũ giúp tính lãi kép ngân hàng. Trong sinh học, số mũ mô tả sự phân chia tế bào hay sự phát triển của vi khuẩn.

Một điều thú vị là khi làm việc với số mũ, ta có thể thực hiện các phép tính nhanh hơn. Thay vì phải nhân từng số một, ta chỉ cần áp dụng các quy tắc về số mũ. Ví dụ: 2³ × 2⁴ = 2⁷, ta chỉ cần cộng các số mũ lại với nhau khi nhân hai số có cùng cơ số.

Các quy tắc cơ bản về số mũ mà bạn cần nắm vững

Số mũ là một khái niệm toán học quan trọng giúp biểu diễn phép nhân lặp lại một số với chính nó. Quy tắc số mũ giúp đơn giản hóa các phép tính phức tạp và là nền tảng cho nhiều ứng dụng trong toán học cao cấp.

Số mũ dương và cách tính số mũ dương

Số mũ dương là gì? Đó là số lần lặp lại phép nhân một số với chính nó. Ví dụ: 2³ = 2 × 2 × 2 = 8. Khi tính toán với số mũ dương, ta luôn nhớ quy tắc: số gốc được nhân với chính nó số lần bằng giá trị số mũ.

Số mũ 0 và ý nghĩa đặc biệt

Số mũ 0 bằng bao nhiêu? Bất kỳ số nào (trừ 0) khi mũ 0 đều bằng 1. Đây là một quy ước quan trọng trong toán học, giúp các công thức tính tổng dãy số trở nên nhất quán và dễ áp dụng.

Số mũ âm và phương pháp tính toán

Số mũ âm là gì? Khi một số có mũ âm, kết quả sẽ bằng 1 chia cho số đó lũy thừa với trị tuyệt đối của số mũ. Ví dụ: 2⁻³ = 1/(2³) = 1/8.

Ví dụ minh họa về cách tính số mũ âm và dương

Để hiểu rõ hơn về công thức số mũ, ta xét ví dụ sau:
2⁴ = 2 × 2 × 2 × 2 = 16
2⁰ = 1
2⁻² = 1/(2²) = 1/4 = 0,25

Việc thực hành thường xuyên với các bài tập đa dạng sẽ giúp nắm vững các quy tắc tính toán với số mũ.

Các công thức số mũ thường gặp và cách áp dụng

Xem thêm : Tổng hợp công thức tổng hiệu và cách tính tổng dãy số cơ bản

Công thức số mũ là gì – đây là những quy tắc tính toán cơ bản với các số hạng có chứa số mũ. Việc nắm vững các công thức này giúp học sinh giải quyết nhanh chóng nhiều bài toán phức tạp hơn.

Công thức nhân hai số mũ cùng cơ số

Khi nhân hai số mũ cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ. Công thức tổng quát:

aᵐ × aⁿ = aᵐ⁺ⁿ

Ví dụ: 2³ × 2⁴ = 2⁷. Cách tính số mũ này giúp rút ngắn thời gian tính toán thay vì phải khai triển từng số hạng.

Công thức chia hai số mũ cùng cơ số

Tương tự như phép nhân, khi chia hai số mũ cùng cơ số, ta giữ nguyên cơ số và trừ số mũ của số bị chia cho số mũ của số chia. Công thức:

aᵐ ÷ aⁿ = aᵐ⁻ⁿ

Phép tính này có mối liên hệ chặt chẽ với phép chia số phức khi áp dụng vào các bài toán nâng cao.

Công thức lũy thừa của một số mũ

Khi tính lũy thừa của một số mũ, ta giữ nguyên cơ số và nhân các số mũ. Công thức:

(aᵐ)ⁿ = aᵐˣⁿ

Các số mũ cơ bản thường xuất hiện trong phép tính này là 2, 3, 4 hoặc các số nguyên dương khác.

Bài tập mẫu về các công thức số mũ cơ bản

Giải bài tập: Tính giá trị của biểu thức (2³)² × 2⁴ ÷ 2³
Bước 1: Áp dụng công thức lũy thừa (2³)² = 2⁶
Bước 2: Biểu thức trở thành 2⁶ × 2⁴ ÷ 2³
Bước 3: Áp dụng công thức nhân và chia: 2⁶⁺⁴⁻³ = 2⁷
Kết quả cuối cùng là 128.

Mối quan hệ giữa số mũ với các khái niệm toán học khác

Số mũ có mối liên hệ mật thiết với nhiều khái niệm toán học quan trọng khác. Việc hiểu rõ các mối quan hệ này giúp chúng ta nắm vững kiến thức và áp dụng hiệu quả trong giải toán. Tôi sẽ phân tích chi tiết từng mối liên hệ để các em dễ dàng tiếp thu.

Số mũ và căn thức – Hai anh em sinh đôi

Xem thêm : Tổng hợp công thức cấp số nhân chính xác nhất

Số mũ và căn thức có mối quan hệ đặc biệt như hai anh em sinh đôi. Khi ta viết a^(1/n), nó chính là căn bậc n của a. Ví dụ: 8^(1/3) = căn bậc 3 của 8 = 2. Điều thú vị là khi ta chuyển đổi qua lại giữa hai dạng này, bài toán trở nên đơn giản hơn rất nhiều.

Số mũ và logarit – Mối liên hệ không thể tách rời

Số mũ và logarit luôn song hành cùng nhau. Nếu a^x = b thì loga(b) = x. Đây là mối quan hệ ngược của nhau, giống như phép cộng và phép trừ vậy. Khi giải các bài toán về công thức tổng n số hạng cấp số cộng, ta thường xuyên sử dụng mối liên hệ này.

Số mũ trong biểu thức phân số

Số mũ và phân số thường xuất hiện cùng nhau trong các biểu thức toán học. Khi làm việc với công thức tính số số hạng cấp số nhân, ta thường gặp các phân số có chứa số mũ. Quy tắc cơ bản là:

(a/b)^n = a^n/b^n

giúp ta đơn giản hóa các phép tính phức tạp.

Ví dụ minh họa về mối liên hệ giữa số mũ và các khái niệm liên quan

Giả sử ta có biểu thức: (8^(1/3))^2 × log2(8)
Bước 1: 8^(1/3) = 2 (dùng mối quan hệ số mũ – căn thức)
Bước 2: 2^2 = 4 (tính số mũ)
Bước 3: log2(8) = 3 (dùng mối quan hệ số mũ – logarit)
Bước 4: 4 × 3 = 12 (kết quả cuối cùng)

Qua ví dụ trên, ta thấy việc nắm vững các mối quan hệ giúp giải quyết bài toán một cách logic và hiệu quả.

FAQ: Câu hỏi thường gặp về số mũ

Số mũ là một khái niệm toán học quan trọng giúp biểu diễn phép nhân lặp lại nhiều lần. Việc hiểu rõ về số mũ sẽ giúp giải quyết nhiều bài toán phức tạp một cách đơn giản hơn. Tôi sẽ giải đáp một số thắc mắc phổ biến về chủ đề này.

Làm thế nào để phân biệt số mũ dương và số mũ âm?

Cách tính số mũ dương rất đơn giản – chỉ cần nhân số gốc với chính nó theo số lần được chỉ định bởi số mũ. Ví dụ: 2³ = 2 x 2 x 2 = 8. Ngược lại, cách tính số mũ âm là lấy 1 chia cho số mũ dương tương ứng. Ví dụ: 2⁻³ = 1/2³ = 1/8. Việc nắm vững quy tắc này sẽ giúp áp dụng công thức bayes hiệu quả hơn trong nhiều bài toán xác suất.

Tại sao số mũ 0 luôn bằng 1?

Bất kỳ số nào (trừ 0) khi lũy thừa với số mũ 0 đều cho kết quả là 1. Điều này xuất phát từ quy tắc chia số mũ: khi ta chia một số cho chính nó (a⁵/a⁵), kết quả luôn là 1. Theo quy tắc số mũ, phép chia này tương đương với a⁵⁻⁵ = a⁰ = 1.

Có thể áp dụng số mũ trong đại số như thế nào?

Số mũ trong đại số được sử dụng rộng rãi để biểu diễn các biểu thức gọn gàng hơn. Thay vì viết x × x × x, ta viết gọn thành x³. Điều này đặc biệt hữu ích khi giải các phương trình mũ, logarit hoặc các bài toán về tăng trưởng theo cấp số nhân. Ví dụ trong tính lãi kép, số tiền sau n năm được tính bằng công thức A = P(1 + r)ⁿ, với P là số tiền gốc và r là lãi suất.

Việc nắm vững các **công thức số mũ** giúp học sinh giải quyết nhiều bài toán một cách nhanh chóng và chính xác. Các quy tắc về số mũ dương, số mũ âm và số mũ 0 tạo nền tảng quan trọng cho việc học tập toán học ở các cấp độ cao hơn. Mối liên hệ chặt chẽ giữa số mũ với căn thức, logarit và phân số là chìa khóa để hiểu sâu về đại số. Những kiến thức này đóng vai trò thiết yếu trong việc phát triển tư duy toán học và ứng dụng thực tiễn.

Nguồn: https://congthuctoan.com
Danh mục: Đại số