Công thức nghiệm pt bậc 2 và cách giải đơn giản cho học sinh yếu

Thầy giáo toán với 30 năm kinh nghiệm hướng dẫn chi tiết **công thức nghiệm pt bậc 2** cùng phương pháp giải đơn giản, dễ nhớ. Bài viết phân tích rõ các trường hợp nghiệm kèm bài tập mẫu giúp học sinh yếu toán nắm vững kiến thức cơ bản này một cách tự nhiên và hiệu quả.

Phương trình bậc 2 là gì và dạng tổng quát của nó?

Phương trình bậc 2 là phương trình có dạng chứa ẩn số x với số mũ cao nhất là 2. Giống như khi chúng ta muốn tính công thức tổng hiệu của hai số, phương trình bậc 2 cũng có một dạng chuẩn để giải quyết mọi bài toán.

Bạn đang xem: Công thức nghiệm pt bậc 2 và cách giải đơn giản cho học sinh yếu

Dạng tổng quát pt bậc 2 được biểu diễn theo công thức:

ax² + bx + c = 0

Trong đó:
– a là hệ số của x², a ≠ 0
– b là hệ số của x
– c là số hạng tự do
– x là ẩn số cần tìm

Ví dụ: 2x² – 5x + 3 = 0 là một phương trình bậc 2 với a = 2, b = -5, c = 3. Khi giải phương trình này, chúng ta sẽ áp dụng các công thức nghiệm để tìm ra giá trị của x thỏa mãn phương trình.

Thầy thường ví von phương trình bậc 2 như một chiếc cầu vồng – đồ thị của nó là một đường parabol uốn cong mềm mại. Điều quan trọng là phải nhận diện được các hệ số a, b, c để áp dụng đúng phương pháp giải phù hợp.

Công thức nghiệm phương trình bậc 2 và cách tính delta

Phương trình bậc 2 là một trong những kiến thức toán học quan trọng mà các em thường gặp khó khăn. Tôi sẽ giúp các em hiểu rõ về công thức nghiệm pt bậc 2 và cách tính delta một cách đơn giản nhất.

Công thức tính delta trong phương trình bậc 2

Delta (Δ) là yếu tố quyết định số lượng nghiệm của phương trình bậc 2. Công thức delta được tính bằng biểu thức:

Δ = b² – 4ac

Xem thêm : Tổng hợp công thức hằng đẳng thức cơ bản và nâng cao chi tiết nhất

Trong đó a, b, c là các hệ số của phương trình ax² + bx + c = 0. Giống như việc tính công thức tổ hợp chỉnh hợp, việc nắm vững công thức tính delta sẽ giúp các em giải quyết bài toán nhanh chóng.

Công thức nghiệm tổng quát của phương trình bậc 2

Sau khi tính được delta, ta có thể xác định nghiệm của phương trình dựa vào 3 trường hợp:
– Nếu Δ > 0: phương trình có 2 nghiệm phân biệt x₁ = (-b + √Δ)/(2a) và x₂ = (-b – √Δ)/(2a)
– Nếu Δ = 0: phương trình có nghiệm kép x = -b/(2a)
– Nếu Δ < 0: phương trình vô nghiệm

Bài tập mẫu 1: Tìm nghiệm phương trình bậc 2 có delta > 0

Giải phương trình: 2x² – 7x + 3 = 0
Ta có: a = 2, b = -7, c = 3
Tính delta: Δ = (-7)² – 4×2×3 = 49 – 24 = 25 > 0
Do Δ > 0 nên phương trình có 2 nghiệm:
x₁ = (7 + 5)/(4) = 3
x₂ = (7 – 5)/(4) = 0,5
Vậy x₁ = 3 và x₂ = 0,5

Bài tập mẫu 2: Tìm nghiệm phương trình bậc 2 có delta = 0

Giải phương trình: x² + 4x + 4 = 0
Ta có: a = 1, b = 4, c = 4
Tính delta: Δ = 4² – 4×1×4 = 16 – 16 = 0
Do Δ = 0 nên phương trình có nghiệm kép:
x = -4/(2×1) = -2
Vậy x = -2

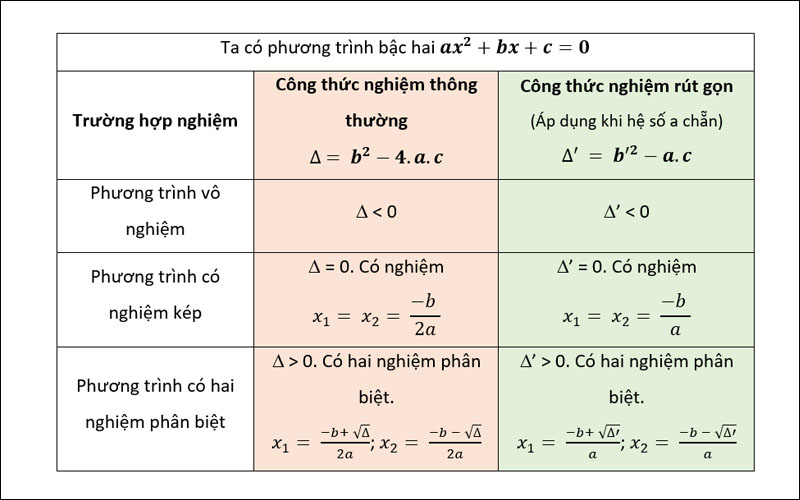
Phân loại nghiệm của phương trình bậc 2 dựa vào delta

Phương trình bậc 2 có thể có 2 nghiệm phân biệt, nghiệm kép hoặc vô nghiệm tùy thuộc vào giá trị của delta (Δ). Tương tự như cấp số cộng là gì, việc phân loại nghiệm giúp học sinh dễ dàng nắm bắt và giải quyết các bài toán.

Trường hợp phương trình bậc 2 có 2 nghiệm phân biệt (Δ > 0)

Khi delta lớn hơn 0, pt bậc 2 có 2 nghiệm phân biệt x1 và x2. Hai nghiệm này được tính theo công thức:

x1 = (-b + √Δ)/(2a) và x2 = (-b – √Δ)/(2a)

Giá trị của hai nghiệm luôn khác nhau và là số thực.

Trường hợp phương trình bậc 2 có nghiệm kép (Δ = 0)

Trường hợp delta bằng 0, pt bậc 2 có nghiệm kép x1 = x2 = -b/(2a). Nghiệm kép có nghĩa là phương trình có một nghiệm duy nhất với bội số bằng 2. Đồ thị parabol trong trường hợp này tiếp xúc với trục hoành tại một điểm.

Trường hợp phương trình bậc 2 vô nghiệm (Δ < 0)

Nếu delta nhỏ hơn 0, pt bậc 2 vô nghiệm trong tập số thực. Điều này có nghĩa là đồ thị parabol không cắt trục hoành tại điểm nào. Phương trình chỉ có nghiệm phức nếu mở rộng tập xác định sang tập số phức.

Ví dụ minh họa cho từng trường hợp

Ví dụ 1: x² – 5x + 6 = 0
Tính delta: Δ = b² – 4ac = 25 – 24 = 1 > 0
Vậy phương trình có 2 nghiệm: x1 = 3 và x2 = 2

Ví dụ 2: x² + 2x + 1 = 0
Tính delta: Δ = 4 – 4 = 0
Vậy phương trình có nghiệm kép: x = -1

Ví dụ 3: x² + x + 1 = 0
Tính delta: Δ = 1 – 4 = -3 < 0
Vậy phương trình vô nghiệm trong tập số thực.

Các phương pháp giải phương trình bậc 2 một ẩn

Phương trình bậc 2 một ẩn có dạng tổng quát

ax² + bx + c = 0 (với a ≠ 0)

là một trong những kiến thức toán học quan trọng. Có hai phương pháp chính để giải loại phương trình này, mỗi phương pháp phù hợp với từng dạng bài tập cụ thể.

Phương pháp giải bằng công thức nghiệm

Xem thêm : Công thức logarit cơ bản và nâng cao dành cho học sinh yếu toán

Công thức nghiệm phương trình bậc 2 là phương pháp phổ biến và hiệu quả nhất. Với phương trình ax² + bx + c = 0, ta tính delta Δ = b² – 4ac rồi áp dụng công thức x = (-b ± √Δ)/2a. Phương pháp này đặc biệt hữu ích khi giải các phương trình có hệ số phức tạp hoặc không thể phân tích thừa số dễ dàng.

Khi áp dụng công thức phương trình tiếp tuyến vào bài toán hình học, ta thường cần kết hợp với việc giải phương trình bậc 2 để tìm điểm tiếp xúc.

Phương pháp giải bằng phân tích thừa số

Phương pháp phân tích thừa số thường áp dụng cho các phương trình có hệ số đơn giản. Ta biến đổi vế trái thành tích các nhân tử bậc nhất, vế phải bằng 0. Phương pháp này thường kết hợp với công thức tính đường sinh khi giải các bài toán hình học không gian.

Bài tập mẫu có lời giải chi tiết

Ví dụ: Giải phương trình 2x² – 5x + 2 = 0

Bước 1: Xác định hệ số
a = 2, b = -5, c = 2

Bước 2: Tính delta
Δ = b² – 4ac = (-5)² – 4×2×2 = 25 – 16 = 9

Bước 3: Tính nghiệm
x₁ = (-(-5) + √9)/(2×2) = (5 + 3)/4 = 2
x₂ = (-(-5) – √9)/(2×2) = (5 – 3)/4 = 1/2

Vậy phương trình có hai nghiệm x₁ = 2 và x₂ = 1/2.

FAQ: Câu hỏi thường gặp về công thức nghiệm phương trình bậc 2

Phương trình bậc 2 là một trong những kiến thức nền tảng quan trọng trong chương trình toán THCS và THPT. Để giúp các em nắm vững kiến thức, tôi sẽ giải đáp một số thắc mắc phổ biến về công thức nghiệm bậc 2 đơn giản.

Làm thế nào để nhớ công thức nghiệm bậc 2 một cách dễ dàng?

Sau nhiều năm giảng dạy, tôi thường hướng dẫn học sinh ghi nhớ công thức nghiệm theo phương pháp “chia để trị”. Đầu tiên, các em chỉ cần nhớ phần tử số là -b cộng/trừ căn delta. Tiếp theo, mẫu số luôn là 2a. Cuối cùng, delta bằng b bình trừ 4ac. Khi chia nhỏ công thức thành 3 phần riêng biệt, việc ghi nhớ sẽ trở nên đơn giản hơn rất nhiều.

Khi nào cần sử dụng công thức nghiệm phương trình bậc 2?

Công thức nghiệm bậc 2 được áp dụng khi phương trình ở dạng chuẩn ax² + bx + c = 0 với a ≠ 0. Đặc biệt, với những phương trình không thể phân tích thành nhân tử hoặc có hệ số phức tạp, cách tìm nghiệm pt bậc 2 bằng công thức là phương pháp hiệu quả và chính xác nhất.

Có cách nào giải phương trình bậc 2 không cần dùng công thức không?

Ngoài công thức nghiệm, phương trình bậc 2 có thể giải bằng phương pháp phân tích thành nhân tử khi các hệ số đơn giản. Ví dụ với phương trình x² – 4x + 4 = 0, ta có thể viết lại thành (x – 2)² = 0, từ đó suy ra x = 2. Tuy nhiên, phương pháp này chỉ phù hợp với một số trường hợp đặc biệt và đòi hỏi kỹ năng quan sát tốt.

Việc nắm vững **công thức nghiệm pt bậc 2** giúp học sinh giải quyết nhiều bài toán trong chương trình phổ thông. Các phương pháp giải phương trình bậc 2 đều dựa trên việc tính delta và áp dụng công thức nghiệm tổng quát. Tùy vào giá trị của delta, phương trình có thể có hai nghiệm phân biệt, nghiệm kép hoặc vô nghiệm. Phương pháp phân tích thừa số cũng là một cách giải hiệu quả trong nhiều trường hợp đặc biệt.

Nguồn: https://congthuctoan.com
Danh mục: Đại số