Tổng hợp công thức hằng đẳng thức cơ bản và nâng cao chi tiết nhất

Thầy hướng dẫn chi tiết các **công thức hằng đẳng thức** từ cơ bản đến nâng cao dành cho học sinh yếu toán. Bài giảng được trình bày đơn giản với nhiều ví dụ minh họa, bài tập mẫu kèm lời giải tỉ mỉ giúp các em dễ dàng nắm vững kiến thức quan trọng này.

Hằng đẳng thức là gì?

Các em học sinh thân mến, thầy đã dạy toán hơn 30 năm và thầy hiểu rằng nhiều em cảm thấy khó khăn với những công thức phức tạp. Thầy sẽ giải thích về hằng đẳng thức một cách đơn giản nhất có thể.

Bạn đang xem: Tổng hợp công thức hằng đẳng thức cơ bản và nâng cao chi tiết nhất

Hằng đẳng thức là một đẳng thức luôn đúng với mọi giá trị của biến trong tập xác định của nó. Giống như một người bạn đáng tin cậy, hằng đẳng thức không bao giờ thay đổi kết quả dù ta có thay đổi giá trị của biến như thế nào.

Ví dụ đơn giản nhất mà các em có thể hình dung là (a + b)² = a² + 2ab + b². Thử nhập các giá trị a = 2, b = 3: (2 + 3)² = 25 và 2² + 2×2×3 + 3² = 4 + 12 + 9 = 25. Kỳ diệu phải không? Điều này luôn đúng với mọi cặp số thực a, b.

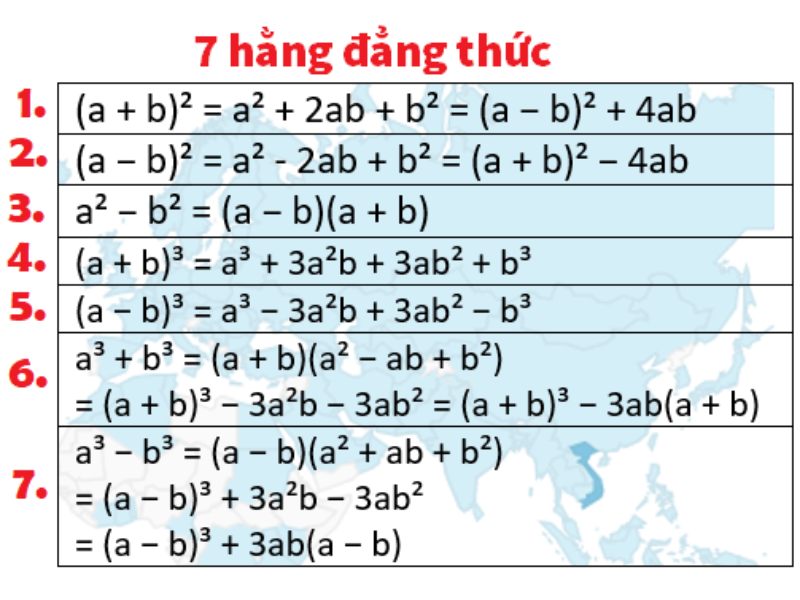
Một số công thức hằng đẳng thức cơ bản mà các em cần ghi nhớ là:

(a ± b)² = a² ± 2ab + b² a² – b² = (a + b)(a – b) (a + b)³ = a³ + 3a²b + 3ab² + b³

Thầy luôn nói với học sinh rằng để nắm vững các hằng đẳng thức đáng nhớ, các em cần thực hành nhiều lần với các số cụ thể. Giống như việc tập đi xe đạp, ban đầu có thể vấp ngã nhưng dần dần sẽ thành thạo.

Các công thức hằng đẳng thức cơ bản và thường gặp nhất

Các hằng đẳng thức cơ bản là những công thức toán học quan trọng, giúp học sinh giải nhanh nhiều dạng bài tập đại số. Tôi thường ví von chúng như những “chìa khóa vạn năng” mở cánh cửa toán học. Sau 30 năm giảng dạy, tôi nhận thấy việc nắm vững các công thức này sẽ giúp các em tự tin hơn khi làm bài.

Hằng đẳng thức bình phương của tổng và hiệu hai số

Hằng đẳng thức bình phương có hai dạng cơ bản:

(a + b)² = a² + 2ab + b²

(a – b)² = a² – 2ab + b²

Để nhớ dễ dàng, các em có thể tưởng tượng: Bình phương của tổng luôn có dấu “+”, còn bình phương của hiệu thì dấu giữa các số hạng sẽ đổi chiều. Khi áp dụng công thức loga kết hợp với các hằng đẳng thức này, chúng ta sẽ giải được nhiều bài toán phức tạp hơn.

Ví dụ minh họa và bài tập áp dụng

Tính giá trị biểu thức: (2x + 3)²
Lời giải:
– Áp dụng công thức (a + b)² với a = 2x và b = 3
– (2x + 3)² = (2x)² + 2(2x)(3) + 3²
– = 4x² + 12x + 9

Hằng đẳng thức lập phương của tổng và hiệu

Hằng đẳng thức lập phương gồm hai công thức:
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a – b)³ = a³ – 3a²b + 3ab² – b³

Bài tập mẫu có lời giải chi tiết

Tính giá trị của (x + 2)³
Lời giải:
– Áp dụng công thức (a + b)³ với a = x và b = 2
– (x + 2)³ = x³ + 3x²(2) + 3x(2)² + 2³
– = x³ + 6x² + 12x + 8

Các dạng hằng đẳng thức quan trọng trong chương trình lớp 8

Trong môn toán lớp 8, công thức hằng đẳng thức lớp 8 đóng vai trò nền tảng giúp học sinh giải quyết nhiều bài toán phức tạp. Các hằng đẳng thức cơ bản sẽ được phân chia thành hai nhóm chính: hằng đẳng thức tổng/hiệu và hằng đẳng thức tích.

Hằng đẳng thức tổng và hiệu các số

Hằng đẳng thức tổng bình phương là một trong những công thức quan trọng giúp học sinh tính toán nhanh chóng. Tương tự như cách áp dụng công thức cấp số cộng, việc nắm vững các hằng đẳng thức tổng sẽ giúp rút ngắn thời gian giải toán đáng kể.

Hằng đẳng thức tích

Hằng đẳng thức tích giúp biến đổi các biểu thức phức tạp thành dạng đơn giản hơn. Khi kết hợp với công thức tính số số hạng cấp số cộng, học sinh có thể dễ dàng giải quyết các bài toán liên quan đến biến đổi đại số.

Phương pháp giải và ví dụ cụ thể

Để áp dụng hiệu quả các hằng đẳng thức, cần thực hiện theo 3 bước:

• Nhận dạng dạng hằng đẳng thức cần sử dụng

• Xác định các thành phần trong biểu thức

• Áp dụng công thức phù hợp

Ví dụ: Khi biến đổi biểu thức (a + b)², ta có:
(a + b)² = a² + 2ab + b²

Với biểu thức (a – b)², kết quả sẽ là:
(a – b)² = a² – 2ab + b²

Ứng dụng của hằng đẳng thức trong đại số và giải toán

Xem thêm : Công thức logarit cơ bản và nâng cao dành cho học sinh yếu toán

Hằng đẳng thức đại số có vai trò quan trọng trong việc giải quyết nhiều bài toán phức tạp. Chúng giúp biến đổi các biểu thức đại số thành dạng đơn giản hơn và chứng minh các bất đẳng thức. Những hằng đẳng thức quan trọng như bình phương của tổng, hiệu hay tam thức bậc hai thường xuyên được áp dụng trong các kỳ thi.

Hằng đẳng thức trong biến đổi đại số

Trong biến đổi đại số, các công thức hằng đẳng thức giúp rút gọn biểu thức phức tạp thành dạng đơn giản. Tương tự như phép nhân số phức, việc áp dụng hằng đẳng thức giúp tính toán nhanh chóng và chính xác hơn. Ví dụ khi tính (a+b)² = a² + 2ab + b², ta không cần phải nhân từng thành phần mà có thể áp dụng trực tiếp công thức.

Hằng đẳng thức trong chứng minh bất đẳng thức

Chứng minh bất đẳng thức là một trong những ứng dụng quan trọng của hằng đẳng thức. Tương tự cách xác định công thức phương trình đường tròn, việc sử dụng hằng đẳng thức giúp chuyển đổi vế trái thành vế phải một cách logic và chặt chẽ. Phương pháp này đặc biệt hiệu quả với các bất đẳng thức có dạng tổng, hiệu của các số không âm.

Bài tập mẫu về chứng minh bất đẳng thức

Ví dụ: Chứng minh rằng với mọi số thực dương a, b ta có: a + b ≥ 2√(ab)

Cách giải:
Áp dụng hằng đẳng thức (a – b)² ≥ 0
⇔ a² – 2ab + b² ≥ 0
⇔ a² + 2ab + b² ≥ 4ab
⇔ (a + b)² ≥ 4ab
⇔ a + b ≥ 2√(ab)

Đây là một ví dụ điển hình về cách vận dụng hằng đẳng thức để chứng minh bất đẳng thức, giúp học sinh hiểu rõ hơn về mối liên hệ giữa các công thức toán học.

FAQ: Câu hỏi thường gặp về hằng đẳng thức

Các hằng đẳng thức phổ biến thường gây khó khăn cho học sinh khi ghi nhớ và vận dụng. Tôi sẽ giải đáp những thắc mắc quan trọng nhất về chủ đề này.

Phân biệt hằng đẳng thức bậc 2 và bậc 3

Hằng đẳng thức bậc 2 và hằng đẳng thức bậc 3 có những điểm khác biệt cơ bản. Với bậc 2, ta thường gặp các biểu thức có số mũ cao nhất là 2 như (a+b)². Còn với bậc 3, số mũ cao nhất là 3 như (a+b)³. Ví dụ điển hình cho bậc 2 là (a+b)² = a² + 2ab + b², còn bậc 3 có dạng (a+b)³ = a³ + 3a²b + 3ab² + b³.

Cách ghi nhớ các hằng đẳng thức phổ biến

Để ghi nhớ các hằng đẳng thức hay gặp, tôi thường hướng dẫn học sinh áp dụng phương pháp “tam giác Pascal”. Với các hằng đẳng thức thường dùng như (a+b)², ta có thể hình dung như một “bánh pizza” chia làm 3 phần: a², 2ab và b². Mỗi phần tương ứng với một hệ số trong tam giác Pascal hàng thứ 2: 1-2-1.

Một cách khác là liên hệ với thực tế. Ví dụ khi tính diện tích hình vuông có cạnh (a+b), ta sẽ được tổng diện tích của 4 phần: hình vuông cạnh a, hình vuông cạnh b và 2 hình chữ nhật kích thước axb. Cách này giúp học sinh hiểu sâu bản chất và nhớ lâu hơn.

Việc nắm vững các **công thức hằng đẳng thức** giúp học sinh phát triển tư duy đại số và kỹ năng biến đổi toán học. Các công thức từ cơ bản đến nâng cao như bình phương, lập phương của tổng hiệu tạo nền tảng quan trọng cho việc học toán ở các cấp độ cao hơn. Thông qua các ví dụ minh họa và bài tập thực hành, học sinh có thể áp dụng thành thạo các hằng đẳng thức vào giải toán và chứng minh bất đẳng thức.

Nguồn: https://congthuctoan.com
Danh mục: Đại số