Tổng hợp công thức lũy thừa và áp dụng giải bài tập đơn giản

Thầy hướng dẫn chi tiết về **công thức lũy thừa** với 30 năm kinh nghiệm giảng dạy. Bài viết trình bày các quy tắc, tính chất cơ bản và trường hợp đặc biệt kèm bài tập mẫu có lời giải chi tiết. Phương pháp giảng dạy đơn giản, dễ hiểu giúp học sinh nắm vững kiến thức quan trọng này.

Lũy thừa là gì và ý nghĩa của công thức lũy thừa trong toán học?

Lũy thừa là phép tính nhân một số với chính nó nhiều lần. Khi bạn thấy một số được viết dưới dạng an, trong đó a là cơ số và n là số mũ, đó chính là lũy thừa. Ví dụ: 23 = 2 × 2 × 2 = 8, số 2 được nhân với chính nó 3 lần.

Bạn đang xem: Tổng hợp công thức lũy thừa và áp dụng giải bài tập đơn giản

Công thức lũy thừa mang ý nghĩa quan trọng trong toán học vì giúp rút gọn cách biểu diễn các phép nhân lặp lại. Thay vì phải viết 2 × 2 × 2 × 2 × 2, ta chỉ cần viết gọn là 25. Điều này giúp việc tính toán trở nên đơn giản và nhanh chóng hơn rất nhiều.

Trong thực tế, lũy thừa xuất hiện ở nhiều lĩnh vực. Ví dụ như trong ngân hàng, lãi kép được tính dựa trên công thức lũy thừa

A = P(1 + r)n

Với P là số tiền gốc, r là lãi suất và n là số năm. Hay trong sinh học, sự phân bào của tế bào cũng tuân theo quy luật lũy thừa cơ số 2, từ 1 tế bào phân thành 2, rồi 4, 8, 16…

Một ứng dụng thú vị khác là trong công nghệ máy tính, dung lượng bộ nhớ thường được tính theo lũy thừa của 2: 1 KB = 210 bytes, 1 MB = 220 bytes. Như vậy, lũy thừa không chỉ là một khái niệm toán học thuần túy mà còn có nhiều ứng dụng thiết thực trong cuộc sống.

Các quy tắc và tính chất cơ bản của công thức lũy thừa

Các quy tắc lũy thừa là nền tảng quan trọng giúp học sinh nắm vững phép tính với số mũ. Tôi thường ví von các quy tắc này như những viên gạch xây dựng nên tòa nhà kiến thức toán học vững chắc. Với hơn 30 năm giảng dạy, tôi nhận thấy việc hiểu rõ các tính chất lũy thừa sẽ giúp các em tự tin giải quyết nhiều dạng bài tập phức tạp hơn.

Quy tắc nhân hai lũy thừa cùng cơ số

Khi nhân hai lũy thừa cùng cơ số, ta chỉ cần giữ nguyên cơ số và cộng các số mũ. Ví dụ:

a^m × a^n = a^(m+n)

Giống như việc gộp hai túi kẹo cùng loại vậy, ta chỉ cần đếm tổng số kẹo là được.

Quy tắc chia hai lũy thừa cùng cơ số

Ngược lại với phép nhân, khi chia hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và trừ số mũ:

a^m ÷ a^n = a^(m-n)

Tôi thường giải thích với học sinh rằng đây giống như việc chia một nhóm học sinh thành các tổ nhỏ hơn.

Quy tắc lũy thừa của một lũy thừa

Khi tính lũy thừa của một lũy thừa, ta nhân các số mũ với nhau:

(a^m)^n = a^(m×n)

Công thức lũy thừa này có thể liên hệ với công thức logarit khi giải các bài toán phức tạp.

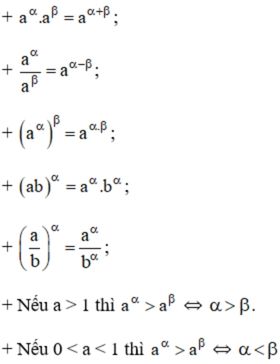
Bài tập mẫu về các quy tắc lũy thừa cơ bản

Ví dụ 1: Tính 2^3 × 2^4
Áp dụng quy tắc nhân: 2^3 × 2^4 = 2^(3+4) = 2^7 = 128

Ví dụ 2: Tính (3^2)^4
Áp dụng quy tắc lũy thừa của lũy thừa: (3^2)^4 = 3^(2×4) = 3^8 = 6561

Những bài tập đơn giản như thế này sẽ giúp các em xây dựng nền tảng vững chắc trước khi tiếp cận các bài toán khó hơn.

Các trường hợp đặc biệt khi tính toán với lũy thừa

Khi làm việc với lũy thừa, có một số trường hợp đặc biệt cần lưu ý để tránh nhầm lẫn. Tương tự như việc tính toán với công thức số phức cơ bản, các quy tắc này giúp chúng ta giải quyết bài toán nhanh chóng và chính xác hơn.

Lũy thừa với số mũ bằng 0

Bất kỳ số nào (trừ số 0) khi lũy thừa với số mũ bằng 0 đều cho kết quả là 1. Điều này có thể gây bất ngờ với nhiều học sinh, nhưng đây là một quy ước quan trọng trong toán học. Lũy thừa số 0 là một khái niệm cần ghi nhớ kỹ để áp dụng trong các phép tính phức tạp hơn.

Lũy thừa với số mũ bằng 1

Khi một số được lũy thừa với số mũ bằng 1, kết quả chính là số đó. Lũy thừa số 1 là trường hợp đơn giản nhất trong các phép tính lũy thừa, giúp ta hiểu rõ hơn về bản chất của phép toán này.

Lũy thừa với số mũ âm

Lũy thừa âm là gì? Đó là phép tính khi số mũ mang giá trị âm, kết quả sẽ bằng 1 chia cho lũy thừa của số đó với số mũ dương tương ứng. Ví dụ: 2^(-3) = 1/(2^3) = 1/8.

Ví dụ minh họa các trường hợp đặc biệt

Để hiểu rõ hơn, ta xét các ví dụ sau:
– 5^0 = 1
– 3^1 = 3
– 2^(-2) = 1/4
– 10^0 = 1

Những ví dụ trên minh họa rõ ràng các quy tắc tính toán với lũy thừa trong trường hợp đặc biệt. Việc nắm vững các quy tắc này sẽ giúp giải quyết nhiều bài toán phức tạp một cách dễ dàng.

Hướng dẫn chi tiết cách tính lũy thừa với các dạng số khác nhau

Xem thêm : Tổng hợp công thức cấp số nhân chính xác nhất

Việc tính toán lũy thừa đóng vai trò quan trọng trong nhiều bài toán. Cách tính lũy thừa cơ bản là nhân liên tiếp một số với chính nó theo số mũ cho trước. Tuy nhiên với mỗi dạng số khác nhau sẽ có những quy tắc riêng cần nắm vững.

Cách tính lũy thừa với số tự nhiên

Lũy thừa số tự nhiên được tính bằng cách nhân liên tiếp số đó với chính nó theo số mũ. Ví dụ: 2³ = 2 x 2 x 2 = 8. Khi gặp số mũ lớn, có thể áp dụng công thức tổng cấp số cộng để tính nhanh hơn.

Cách tính lũy thừa với số thập phân

Lũy thừa số thập phân cần chú ý đến vị trí dấu phẩy. Quy tắc là đếm tổng số chữ số thập phân của các thừa số rồi đặt dấu phẩy vào kết quả. Ví dụ: 0,1² = 0,01 vì 0,1 có 1 chữ số thập phân nên kết quả có 2 chữ số thập phân.

Cách tính lũy thừa bậc n

Lũy thừa bậc n là trường hợp tổng quát với số mũ n bất kỳ. Khi n là số âm, kết quả bằng 1 chia cho lũy thừa của số đối của n. Với n phức tạp, có thể áp dụng công thức tổ hợp để giải quyết.

Bài tập thực hành có lời giải

Bài 1: Tính 2⁴
Lời giải: 2⁴ = 2 x 2 x 2 x 2 = 16

Bài 2: Tính 0,2³
Lời giải: 0,2³ = 0,2 x 0,2 x 0,2 = 0,008
(0,2 có 1 chữ số thập phân nên kết quả có 3 chữ số thập phân)

Bài 3: Tính (-2)³
Lời giải: (-2)³ = (-2) x (-2) x (-2) = -8
(Số âm mũ lẻ cho kết quả âm)

Bảng tổng hợp các công thức lũy thừa thường gặp

Các bảng công thức lũy thừa giúp học sinh nắm vững và vận dụng hiệu quả kiến thức về lũy thừa trong toán học. Tương tự như cách tính trung bình cộng là gì, việc nắm chắc các công thức lũy thừa sẽ giúp giải quyết nhiều bài toán phức tạp một cách đơn giản hơn.

Công thức lũy thừa cơ bản

Công thức lũy thừa cơ bản bao gồm các quy tắc tính toán với số mũ. Khi nhân hai lũy thừa cùng cơ số, ta cộng số mũ. Khi chia hai lũy thừa cùng cơ số, ta trừ số mũ. Với lũy thừa của tích, ta nhân các lũy thừa của từng thừa số. Đặc biệt, mọi số mũ 0 đều bằng 1 và số mũ âm bằng nghịch đảo của số mũ dương tương ứng.

Công thức lũy thừa nâng cao

Các lũy thừa cơ bản phát triển thành những công thức phức tạp hơn khi áp dụng vào đại số. Lũy thừa của một biểu thức, lũy thừa của thương, hay lũy thừa của lũy thừa đều tuân theo những quy tắc nhất định. Một số công thức quan trọng như (a^m)^n = a^(m×n) hay (ab)^n = a^n × b^n thường xuyên xuất hiện trong các bài toán.

Ví dụ áp dụng bảng công thức

Giả sử cần tính (2^3)^2, ta áp dụng công thức (a^m)^n = a^(m×n). Do đó (2^3)^2 = 2^(3×2) = 2^6 = 64. Tương tự, khi tính (3×4)^2, ta có thể dùng công thức (ab)^n = a^n × b^n. Vậy (3×4)^2 = 3^2 × 4^2 = 9 × 16 = 144. Những ví dụ này cho thấy việc nắm vững công thức giúp tính toán nhanh chóng và chính xác.

FAQ: Câu hỏi thường gặp về công thức lũy thừa

Việc nắm vững công thức lũy thừa là gì và cách áp dụng đúng sẽ giúp học sinh giải quyết nhiều bài toán phức tạp. Dưới đây là một số câu hỏi phổ biến về công thức tính lũy thừa và cách sử dụng hiệu quả.

Làm thế nào để ghi nhớ công thức lũy thừa hiệu quả?

Sau nhiều năm giảng dạy, tôi thường khuyên học sinh ghi nhớ công thức lũy thừa bằng phương pháp “3T”: Thực hành – Tưởng tượng – Thường xuyên. Thực hành giải nhiều bài tập đa dạng, tưởng tượng các tình huống thực tế liên quan đến lũy thừa như tăng trưởng dân số, và thường xuyên ôn tập để củng cố kiến thức. Một cách hiệu quả khác là liên hệ các công thức với hình ảnh trực quan, ví dụ: a² là diện tích hình vuông cạnh a.

Có những lỗi sai phổ biến nào khi sử dụng công thức lũy thừa?

Qua kinh nghiệm chấm bài, tôi nhận thấy học sinh thường mắc 3 lỗi cơ bản: nhầm lẫn giữa (a+b)² và a²+b², quên quy tắc dấu khi lũy thừa số âm với số mũ chẵn/lẻ, và áp dụng sai quy tắc với số mũ 0. Một số em còn nhầm lẫn khi tính (a.b)ⁿ thành aⁿ.bⁿ⁺¹. Để tránh những sai lầm này, cần hiểu rõ bản chất của từng công thức và kiểm tra kỹ kết quả.

Khi nào nên sử dụng máy tính để tính lũy thừa?

Máy tính nên được sử dụng khi làm việc với các số mũ lớn hoặc các phép tính phức tạp như căn bậc cao của lũy thừa. Tuy nhiên, với các bài toán cơ bản có số mũ nhỏ (2, 3, 4), học sinh cần rèn luyện kỹ năng tính nhẩm để phát triển tư duy toán học. Việc phụ thuộc quá nhiều vào máy tính có thể làm giảm khả năng tư duy logic và ước lượng kết quả.

Việc nắm vững các **công thức lũy thừa** tạo nền tảng quan trọng trong học tập toán học. Các quy tắc tính toán với lũy thừa như nhân, chia cùng cơ số và các trường hợp đặc biệt với số mũ 0, 1 hay âm đều có ứng dụng thiết thực. Thông qua các ví dụ minh họa và bài tập thực hành, người học có thể áp dụng thành thạo công thức vào giải toán. Kiến thức về lũy thừa là cơ sở để tiếp cận các phép toán phức tạp hơn trong chương trình toán học các cấp.

Nguồn: https://congthuctoan.com
Danh mục: Đại số