Lý thuyết công thức tỉ lệ thuận Toán lớp 7

Công thức tỉ lệ thuận thuộc chương trình học lớp 7. Đây là phần kiến thức mà học sinh cần nhớ để biết cách áp dụng vào bài tập một các hiệu quả.

Định nghĩa

Định nghĩa về công thức tỉ lệ thuận cho rằng: Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx (với k là hằng số khác 0) thì ta nói y tỉ lệ thuận với x theo hằng số tỉ lệ k.

Bạn đang xem: Lý thuyết công thức tỉ lệ thuận Toán lớp 7

Khi đại lượng y tỉ lệ thuận với đại lượng x (theo hệ số k, ≠ 0) thì x cũng tỉ lệ thuận với y.  Ta nói hai đại lượng đó tỉ lệ thuận với nhau và theo hệ số tỉ lệ 1/k.

Tính chất

Nếu hai đại lượng tỉ lệ thuận với nhau, ta có:

• Tỉ số hai giá trị tương ứng của chúng luôn không đổi (bằng hệ số tỉ lệ):

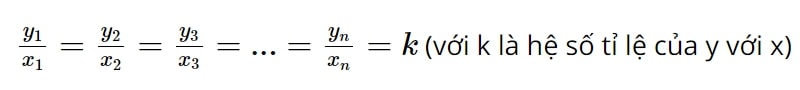
• Tỉ số giữa hai giá trị bất kỳ của đại lượng này bằng tỉ số giữa hai giá trị tương ứng của đại lượng kia:

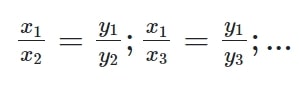Ví dụ minh họa

Ví dụ 1: Cho x và y là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ là -2. Hãy biểu diễn y theo x.

Đáp án: Ta có: x và y là hai đại lượng tỉ lệ thuận theo hệ số tỉ lệ là -2 nên y cũng tỉ lệ thuận với x theo hệ số tỉ lệ là -½.

Khi đó suy ra: y = -x/2.

Ví dụ 2: Cho x và y là hai đại lượng tỉ lệ thuận với nhau theo hệ số tỉ lệ k. Ta có x = 12 thì y = -3. Tìm hệ số k?

Đáp án: x và y là hai đại lượng tỉ lệ thuận với nhau theo hệ số tỉ lệ k nên suy ra x = ky.

Ta có: 12 = k(-3) ⇒ k = -4 Hay x = -4y.

Bài tập ôn tập

Học sinh có thể chủ động giải đề khi ở nhà để ôn luyện kiến thức trước khi đến lớp. Điều này có thể giúp bạn ghi nhớ và biết cách áp dụng công thức hiệu quả hơn.

Bài tập

Một số bài tập ôn tập bao gồm:

Bài 1: Cho hai đại lượng x và y tỉ lệ với nhau. Biết x₁ = 3; y₁ = 6. Tính hệ số tỉ lệ của y đối với x trong các trường hợp:

1. Khi y tỉ lệ thuận với x.
2. Khi y tỉ lệ nghịch với x.

Bài 2: Cho x và y tỉ lệ thuận với nhau và khi x = 8 thì y = 12. Thực hiện các phép tính:

1. Tìm hệ số tỉ lệ k của y đối với x và biểu diễn y theo x.
2. Tính giá trị của y khi x = 2; x = -4.

Xem thêm : Hướng dẫn công thức tổ hợp và chỉnh hợp cho học sinh trung học phổ thông

Bài 3: Cho x và y tỉ lệ nghịch với nhau và khi x = 6 thì y = 15. Thực hiện các phép tính:

1. Tìm hệ số tỉ lệ của y đối với x.
2. Biểu diễn y theo x.
3. Tính giá trị của y khi x = 3; x = -45.

Bài 4: Cho biết rằng, cứ 100kg thóc sẽ cho ra 70kg gạo. Vậy 2 tấn thóc thì cho bao nhiêu kg gạo?

Bài 5: Cho biết x và y là hai đại lượng tỉ lệ thuận:

a. Xác định hệ số tỉ lệ của y đối với x.

b. Điền những số thích hợp vào ô trống.

Đáp án

Học sinh có thể tham khảo đáp án và cách giải sau đây để kiểm tra kết quả bài làm của mình.

Bài 1:

a. Vì y và x tỉ lệ thuận, nên ta có hệ số tỉ lệ là:

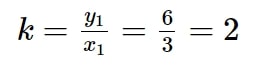
Từ đó suy ra, vậy 2 là hệ số tỉ lệ khi y tỉ lệ thuận với x.

b. Vì y và x tỉ lệ thuận, nên ta có hệ số tỉ lệ là:

a = x₁.y₁ = 3.6 = 18

Từ đó suy ra, 18 là hệ số tỉ lệ khi y tỉ lệ nghịch với x.

Bài 2:

a. Ta có  x và y tỉ lệ thuận với nhau nên theo công thức hệ số tỉ lệ:

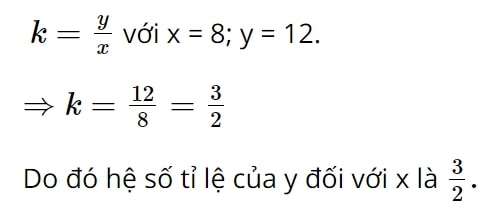
b.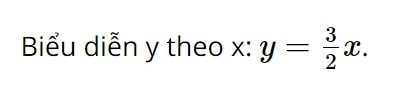

Bài 3:

a. Ta có x và y tỉ lệ nghịch với nhau nên hệ số tỉ lệ của y đối với x là: a = xy.

Với x = 6; y = 15

⇒ 6.15 = 90.

Vậy hệ số tỉ lệ y đối với x là 90.

b.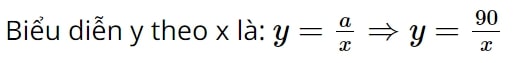

c.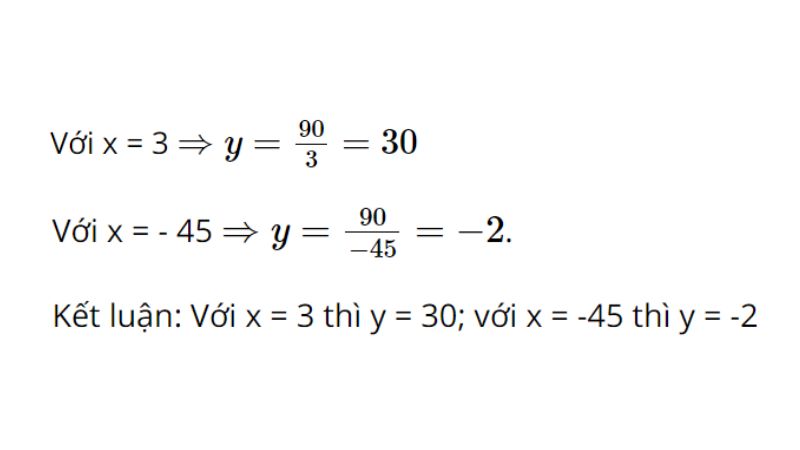

Bài 4:

Bài 5:

Trên đây là một số bài tập ví dụ minh họa có áp dụng công thức tỉ lệ thuận. Nội dung kiến thức này nằm trong chương trình Toán lớp 7 mà học sinh cần chú ý ôn tập để hiểu và biết cách áp dụng vào bài làm.

Kết luận

Công thức tỉ lệ thuận được giải đáp một cách dễ hiểu và dễ nhớ cho học sinh. Bạn có thể chủ động ôn tập tại nhà bằng cách luyện tập thực hành giải bài tập. Điều này sẽ giúp bạn ghi nhớ và dễ dàng đạt điểm cao trong phần nội dung kiến thức này.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê