Nhận bản tin
Nhận các thông tin từ chúng tôi nhập email này ngay
Công Thức Nguyên Hàm Đầy Đủ Và Chính Xác Nhất
Nắm công thức nguyên hàm giúp học sinh có thể làm bài tập và vượt qua bài thi dễ dàng hơn. Kiến thức này khá rộng và tạo thử thách lớn, đòi hỏi bạn phải tìm hiểu kỹ để nắm được cách giải bài tập chuẩn hơn.
Nguyên hàm là gì?
Nguyên hàm của hàm số thực cho trước f là số F có đạo hàm bằng f, tức là F’ = f. Cho hàm số f xác định trên K, nguyên hàm của hàm số này trên K tồn tại khi F(x) tồn tại trên K. F’(x) = f(x) (Với x thuộc K).
Ví dụ: Hàm f(x) = cosx có nguyên hàm F(x) = sinx vì (sinx)’ = cosx.
Tính chất của các công thức nguyên hàm
Với 2 hàm số liên tục g, k trên K:

Bảng công thức nguyên hàm
Cập nhật công thức tính nguyên hàm được tổng hợp theo bảng giúp học sinh có thể giải bài dễ dàng hơn.
1. Nguyên hàm công thức cơ bản
Các công thức nguyên hàm cơ bản được tổng hợp đầy đủ và chi tiết theo bảng:


2. Công thức tính nguyên hàm nâng cao
Ngoài những công thức cơ bản, bạn cũng nên chú ý các công thức nâng cao:


Phương pháp tính nguyên hàm nhanh nhất
Để việc học trở nên dễ dàng hơn đối với công thức nguyên hàm. Học sinh nên chú ý học hỏi thêm những phương pháp giải bài thích hợp. Một số dạng bài thường gặp được tổng hợp chi tiết.
Cách 1: Giải bài tập công thức nguyên hàm từng phần
Giải dạng bài tập này, bạn cần nắm được định lý cơ bản:
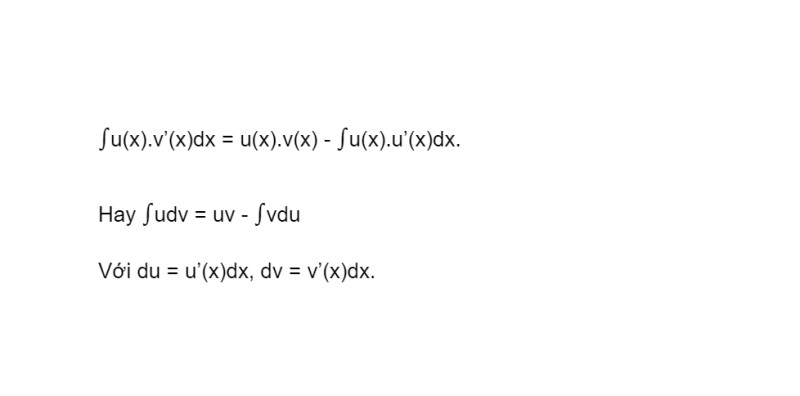
Xét 4 trường hợp tính nguyên hàm từng phần, P(x) là đa thức theo ẩn x.
Để hiểu hơn cách giải này, học sinh có thể tìm hiểu theo ví dụ minh họa. Bạn giải bài tìm nguyên hàm của hàm số xsinxdx. Học sinh theo dõi cách giải chi tiết theo hình minh họa.
Cách 2: Giải dạng bài tính nguyên hàm hàm số lượng giác
Dạng bài tập thường gặp tiếp theo là nguyên hàm lượng giác. Với loại nguyên hàm này có thể chia thành nhiều dạng.
Dạng 1: I = dx/[sin(x+a)sin(x+b)]

Bạn có thể tham khảo minh họa cho kiểu bài này để tìm ra cách giải.

Dạng 2: I = tan(x + a)tan(x + b)dx
Phương pháp tính được mô tả theo hình minh họa:

Ví dụ minh họa và cách tính với vài tập mẫu tìm nguyên hàm K = tan(x + 3cot(x + 6)dx.
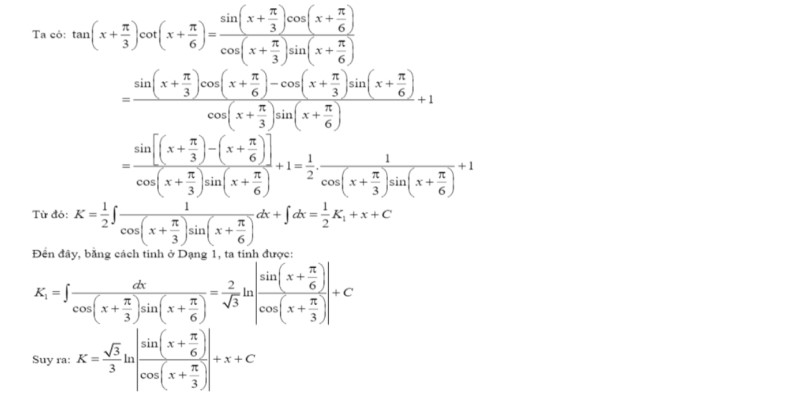
Dạng 3: I = dx/(asinx + bcosx)
Với dạng bài này, học sinh tham khảo cách tính và ví dụ minh họa khi giải bài.

Dạng 4: Tính nguyên hàm của I = dx/(asinx +bcosx + c)

Phương pháp giải bài tập và ví dụ minh họa giải bài
Cách 3: Cách tính nguyên hàm số mũ

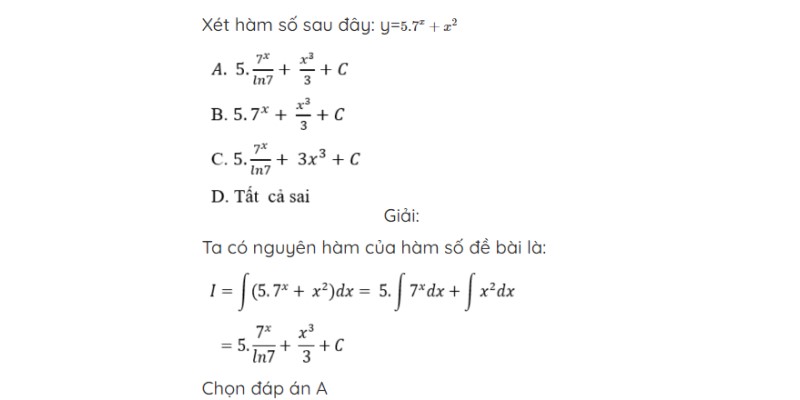
Cách 4: Cách tính nguyên hàm đặt ẩn dụ (Dạng bài đổi biến số)
Giải bài tập bày có dạng mẫu được đưa ra gồm:
- f(x)dx = F(x) + C và u = (x) là hàm số đạo hàm có f(u)du = F(u) + C.
- Nếu F(x) liên tục, đặt x = (t), với (t) cùng với đạo hàm là ‘(t) là những hàm số liên tục sẽ được f(x) = f((t).'(t)dt.
Thông qua phương pháp chung, học sinh tiến hành tìm hiểu các dạng bài thường gặp và nắm cách đọc.


Kết luận
Nắm rõ công thức nguyên hàm giúp học sinh có thể giải bài dễ dàng, tránh nhầm lẫn giữa các dạng khác nhau. Bạn có thể tìm hiểu về cách giải bài hay, có kết quả học tập tốt hơn.
Nguồn: https://congthuctoan.com
Danh mục: Giải tích
Bài viết liên quan

Các công thức số phức và phương pháp giải toán từ cơ bản đến nâng cao
Tìm hiểu các công thức số phức từ cơ bản đến nâng cao với phương pháp giải chi tiết, dễ hiểu. Bao gồm dạng đại số, lượng giác và ứng dụng trong hình học, vật lý điện học.

Khám phá công thức lim và phương pháp tính giới hạn hàm số cơ bản
Tìm hiểu các công thức lim từ cơ bản đến nâng cao với phương pháp giải chi tiết. Hướng dẫn tính lim một phía, lim vô cùng và xử lý dạng vô định kèm bài tập mẫu dễ hiểu.

Tìm hiểu công thức tích phân từng phần và phương pháp giải chi tiết
Tìm hiểu chi tiết công thức tích phân từng phần với phương pháp udv đơn giản, dễ hiểu. Hướng dẫn cách tính, các dạng bài tập thường gặp kèm lời giải cụ thể cho học sinh.

Công thức tích phân đầy đủ Và chính xác nhất
Khám phá công thức tích phân giúp bạn tiếp cận môn toán học dễ dàng hơn. Khái niệm này được ứng dụng trong nhiều lĩnh vực trong đời sống, có liên quan đến tính diện tích, khối lượng, tỉ suất thay đổi một lượng hoặc đạo hàm của hàm số.Có thể bạn quan tâm Công […]
Công Thức Đạo Hàm Nhanh Của Hàm Số Thường Gặp
Nghiên cứu công thức đạo hàm nhanh giúp bạn giải quyết các bài toán nhanh chóng. Với cách nhìn toàn diện về công thức tính nhanh, bạn có thể giải quyết các dạng của hàm số lượng giác, đa thức, mũ logarit.Có thể bạn quan tâm Công thức tích phân đầy đủ Và chính xác […]
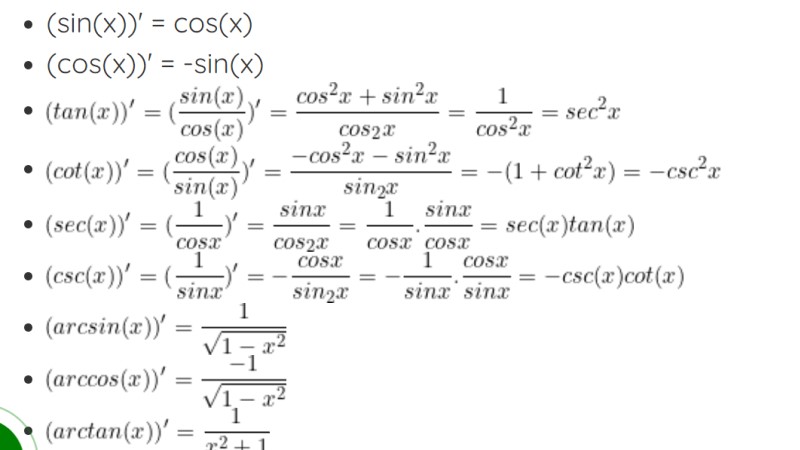
Tổng hợp công thức đạo hàm cơ bản đầy đủ nhất
Nắm công thức đạo hàm và đạo hàm lượng giác giúp bạn tổng hợp và nắm kiến thức đầy đủ hơn. Học theo bảng tổng hợp, bạn có thể giải bài tập dễ dàng, ứng dụng hiệu quả trong quá trình giải toán.Có thể bạn quan tâm Tìm hiểu công thức tích phân từng phần […]

