Công thức hạ bậc là gì? Tổng hợp công thức hạ bậc lượng giác

Công thức hạ bậc là một trong những khái niệm quan trọng bậc nhất của bộ môn Lượng giác. Nắm vững kiến thức này giúp bạn nhanh chóng giải được các bài về tích phân cũng như các phương trình phức tạp.

Định nghĩa công thức hạ bậc là gì và ý nghĩa

Công thức hạ bậc là công cụ để chuyển đổi các biểu thức bậc cao về bậc thấp hơn trong Lượng giác. Nghĩa là nó giúp biến một phương trình phức tạp trở thành phương trình đơn giản.

Bạn đang xem: Công thức hạ bậc là gì? Tổng hợp công thức hạ bậc lượng giác

Việc tối ưu biểu thức về bậc nhất với Sin và Cos sẽ giảm đi công sức và thời gian để giải bài tập. Bạn có thể áp dụng vào quá trình học tích phân hay các bài lượng giác có đề dài.

Công thức cơ bản nhất đó là biến đổi Sin bình phương và Cos bình phương, có dạng:

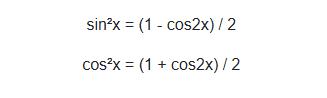
Bạn sẽ thấy công thức này xuất hiện rất nhiều trong các bài tập về phương trình lượng giác. Phổ biến nhất là giải phương trình luôn đúng với mọi x:

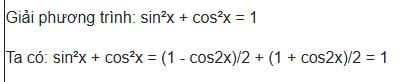
Khi ứng dụng, trước Sin và Cos sẽ có thêm tiền tố để yêu cầu người giải tính tích phân. Hoặc đôi khi đó là các bài chứng minh đẳng thức là những bài lấy điểm khá, điểm giỏi.

Công thức lượng giác hạ bậc có trong chương trình lớp mấy?

Lượng giác nằm trong sách giáo khoa Toán học Đại số của lớp 11 – Trung học phổ thông. Phân bổ chương trình được thực hiện theo Thông tư 32/2018/TT-BGDĐT được ban hành vào năm 2018.

Không chỉ có hạ bậc mà còn có các bài khác về lĩnh vực này của Toán học như:

• Góc lượng giác;
• Số đo các góc và giá trị, quan hệ của giá trị;
• Đường tròn lượng giác;
• Công thức biến đổi như cộng, đổi tích thành tổng và ngược lại, công thức nhân đôi lượng giác.

Tổng hợp công thức hạ bậc lượng giác cần thiết nhất

Công thức sẽ được phân chia cụ thể để học sinh dễ nắm bắt hơn khi làm bài tập. Dựa trên bậc của Sin và Cos mà sẽ có hạ bậc 2, bậc 3, bậc 4 và bậc 5.

Bậc 2

Xem thêm : Hướng dẫn học công thức biến đổi tích thành tổng và bài tập

Công thức hạ bậc bậc 2 nghĩa là hạ từ bậc 2 xuống bậc nhất:

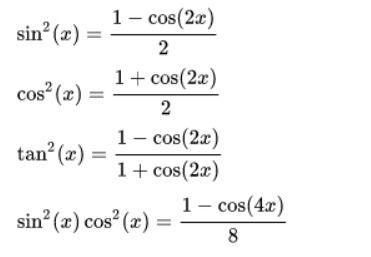
Hoặc có thể viết dưới dạng là:

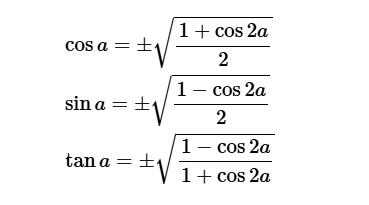
Ví dụ minh hoạ:

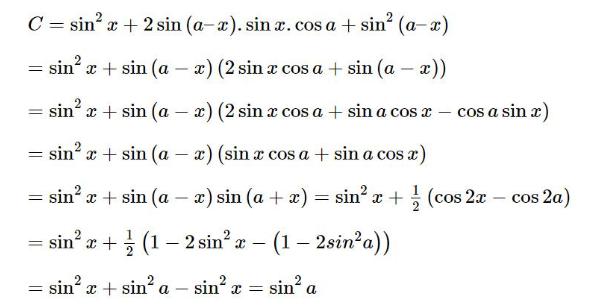
Bậc 3

Công thức này hạ hàm từ bậc 3 xuống còn bậc 2 để giảm tính phức tạp của phương trình:

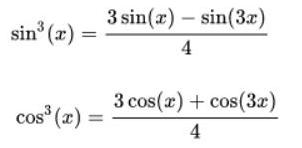
Hoặc viết dưới dạng:

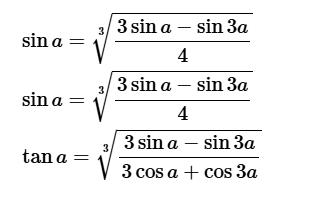
Ví dụ bài tập công thức này:

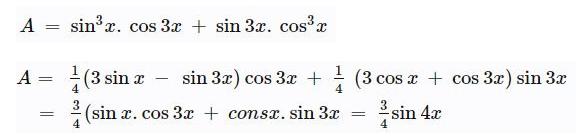
Bậc 4

Công thức hạ hàm từ bậc 4 về bậc 3 hoặc các bậc nhỏ hơn để giải tích phân:

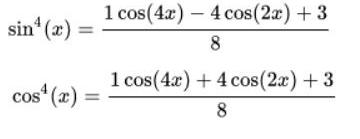
Dạng khác của công thức hạ bậc lượng giác này:

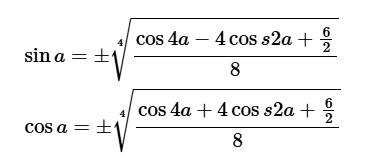
Ví dụ:

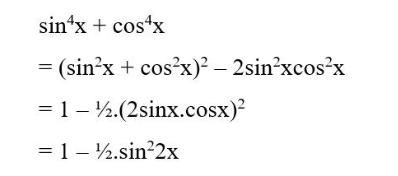
Bậc 5

Công thức này không được áp dụng phổ biến trong các bài tập lượng giác vì bậc quá lớn. Thông thường nó chỉ xuất hiện trong đề thi học sinh giỏi hoặc học nâng cao:

Ví dụ minh hoạ:

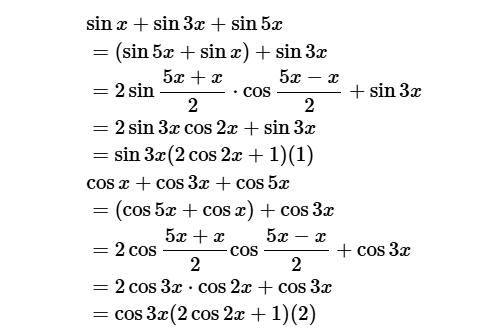
Kết luận

Công thức hạ bậc là kiến thức học sinh nhất định phải nắm vững khi học Lượng giác. Bài tập về phần này tương đối khó nên nếu không chăm chỉ ôn luyện có thể gặp thử thách khi giải.

Nguồn: https://congthuctoan.com
Danh mục: Lượng giác