Tổng hợp công thức cấp số nhân chính xác nhất

Công thức cấp số nhân là nội dung kiến thức quan trọng trong chương trình học THPT. Đây là phần kiến thức phức tạp khiến nhiều học sinh gặp khó khăn khi ghi nhớ và vận dụng vào bài tập. Do đó, Congthuctoan sẽ giúp bạn tổng hợp nội dung cơ bản, giúp bạn hiểu và biết cách áp dụng công thức này.

Định nghĩa cấp số nhân

Cấp số nhân là một dãy số (vô hạn hoặc hữu hạn) thỏa mãn đủ điều kiện. Kể từ số hạng thứ hai, mỗi số hạng là tích của số hạng đứng ngay trước đó và một số cố định gọi là hằng số. Hằng số này được gọi là công bội của cấp số nhân (ký hiệu là q).

Bạn đang xem: Tổng hợp công thức cấp số nhân chính xác nhất

Công thức tính tổng cấp số nhân:

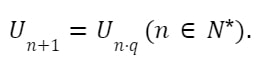
Trong đó:

• U_n: cấp số nhân
• q: công bội
• n ∈ N*

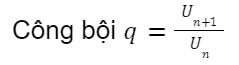
Ví dụ 1: Cho cấp số nhân U₃ = 8, U₄ = 16. Tính công bội q.

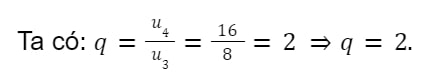
Ví dụ 2: Cho cấp số nhân thỏa mãn u₁ = 5, q = 3. Tính u₂.

Ta có: u₂ = qu₁ = 3.5 = 15 ⇒ u₂ = 15.

Tính chất cấp số nhân

Cấp số nhân (U_n) từ số hạng thứ hai, bình phương của mỗi số hạng (trừ số hạng cuối đối với cấp số nhân hữu hạn) sẽ bằng tích của số đứng trước và số đứng ngay sau nó.

⇔ (u_k)² = u_{k – 1}.u_{k + 1}

Nếu cấp số nhân (u_n) có số hạng u₁ và công bội q thì số hạng tổng quát u_n sẽ được tính theo công thức: u_n = u_1.q^n-1.

Ví dụ: Cho u_n và q > 0. Biết u₁ = 1 và u₃ = 3. Tìm u₄.

Bài giải tham khảo:

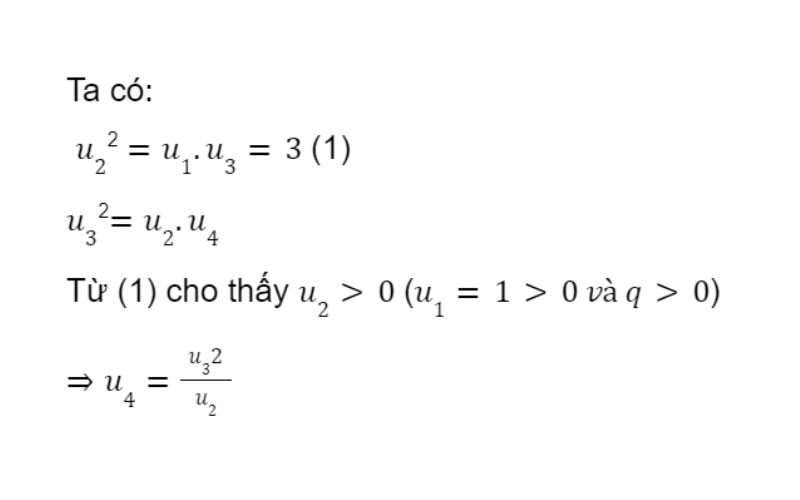
• Khi q = 0, dãy có dạng u₁; 0; 0…;0;… và S_n = u₁.
• Khi q = 1, dãy có dạng u₁; u₁; u₁;…; u₁;… và S_n = nu₁.
• Khi u₁ = 0 (với mọi q), cấp số nhân có dạng 0; 0; 0;…;0;… và S_n = u₁.

Công thức tính cấp số nhân cơ bản

Tổng hợp 5 công thức tổng cấp số nhân cơ bản chuẩn xác nhất. Bạn có thể tham khảo để biết cách áp dụng giải bài tập. Công thức cụ thể kèm ví dụ minh họa bao gồm:

Dạng 1: Công thức nhận biết cấp số nhân

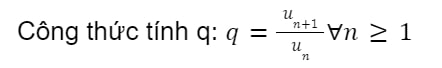
• Nếu q không đổi, dãy u_n là cấp số nhân.
• Nếu q thay đổi, dãy u_n không phải cấp số nhân.

Ví dụ: Cho một cấp số nhân có số hạng thứ nhất là 2, công bội là 2. Hãy viết 6 số hạng đầu tiên.

Đáp án: 6 số hạng đầu tiên lần lượt là 2, 4, 8, 16, 32, 64.

Dạng 2: Công thức tìm công bội cấp số nhân

Ta sử dụng công thức cấp số nhân cấp số cộng và các tính chất của cấp số nhân, biến đổi để tìm công bội của cấp số nhân. Cụ thể như sau:

Ví dụ: Cho cấp số nhân U_n có u₁ = 2, u₂ = 4. Tìm công bội q.

Áp dụng công thức q = u₂/u₁ = 4/2 = 2 ⇒ q = 2.

Dạng 3: Công thức tìm số hạng cấp số nhân

Để tìm số hạng cấp số nhân, ta có thể sử dụng công thức tính số hạng tổng quát.

Un = U₁.q_n-1, n ≥ 2.

Ví dụ: Cho cấp số nhân với u₃ = 8, u₅ = 32. Tìm số hạng thứ 10 của cấp số nhân.

Đáp án:

Gọi q là công bội của cấp số nhân ⇒ q²=u₅ ÷ u₃ = 4 ⇒ q = ±2.

Với q = 2 ⇒ u₁₀ = u₃.q⁷ = 8.2⁷ = 1024

Với q = -2 ⇒ u₁₀ = u₃.q7 = 8.(-2)⁷ =  -1024

Dạng 4: Công thức tính tổng cấp số nhân của n số hạng đầu tiên trong dãy

Xem thêm : Tổng hợp công thức hằng đẳng thức cơ bản và nâng cao chi tiết nhất

Để tính tổng cấp số nhân của n số hạng đầu tiên trong dãy số, ta áp dụng công thức:

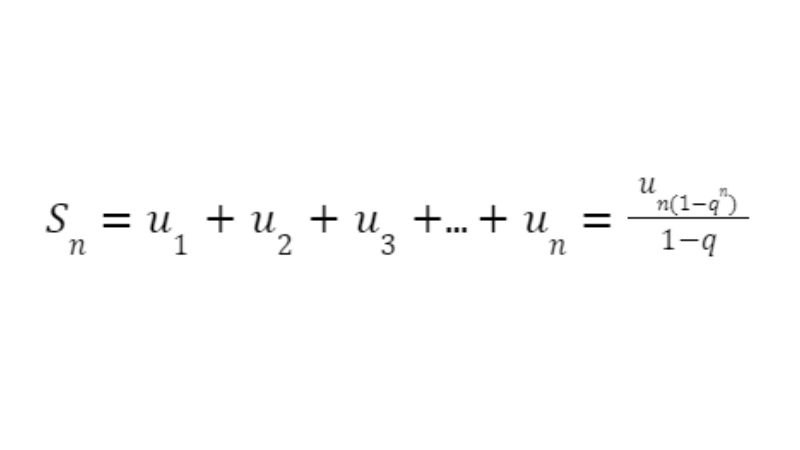
Ví dụ: Tính tổng cấp số nhân của dãy số:

S = 2 + 6 + 18 + 13122

Đáp án: Ta có (U_n) gồm u₁ = 2 và q = 3

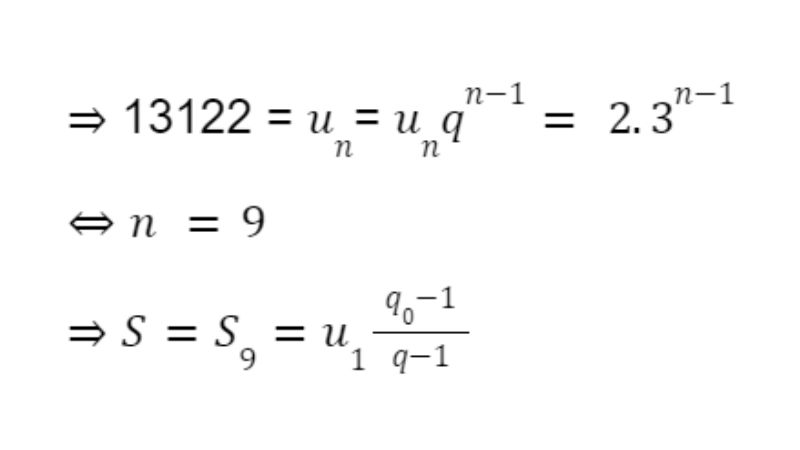
Dạng 5: Công thức tìm cấp số nhân

Để tìm cấp số nhân, ta cần xác định được thành phần cấu tạo nên một cấp số nhân. Các thành phần bao gồm số hạng đầu U₁, và công bội q. Biết được chúng, ta có thể suy ra công thức cho số hạng tổng quát.

Ví dụ: Xác định cấp số nhân gồm 6 số hạng, biết tổng của 5 số hạng đầu là 31 và tổng 5 số hạng sau là 62.

Đáp án: Gọi cấp số nhân cần tìm có công bội q và số hạng đầu là u_n.

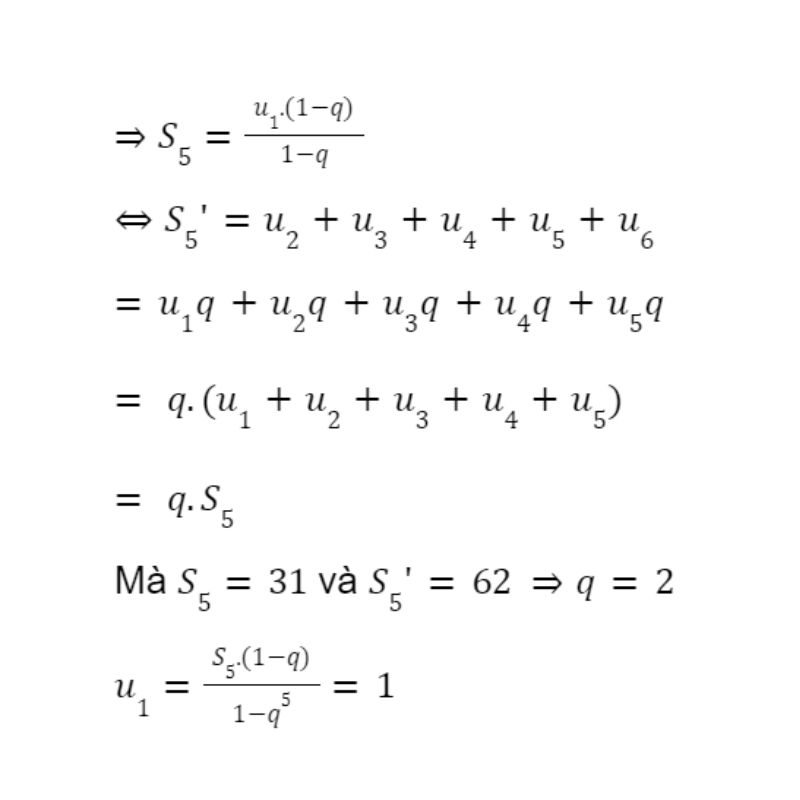
⇒ Cấp số nhân là các số 1; 2; 4; 8; 16; 32.

Định nghĩa cấp số nhân lùi vô hạn

Cấp số nhân lùi vô hạn là khi cấp số nhân (U_n) có công bội q thỏa mãn điều kiện -1 < q < 1.

Sn = u₁(1 – qⁿ)(1 – q) = u₁(qⁿ – 1)(q – 1)

Trong đó: S_n là tổng n số hạng đầu tiên của cấp số nhân.

Ví dụ: 1/3; 1/9; 1/27;1/81;1/243 là cấp nhân lùi vô hạn q = 1/3.

Kết luận

Kiến thức về công thức cấp số nhân được tổng hợp chi tiết cho bạn dễ dàng tìm hiểu. Nắm được nội dung phần này sẽ giúp ích cho bạn trong quá trình học tập hiệu quả hơn.

Nguồn: https://congthuctoan.com
Danh mục: Đại số