Công thức Viet và ứng dụng trong Toán
Công thức Viet là kiến thức quan trọng trong chương trình học lớp 9 hiện nay. Học sinh cần nắm vững để biết phương pháp giải và ứng dụng vào bài tập.
Khái niệm hệ thức Viet
Định lý Viet hay hệ thức Viet (Viète) là công thức Toán học do nhà toán học Pháp François Viète tìm ra. Đây là công thức tính thể hiện quan hệ giữa các nghiệm của phương trình đa thức (trong trường số phức) và các hệ số của nó.
Định lý này là kiến thức trọng tâm trong chương trình Toán học đại số ở cấp 2 và cấp 3.

Định lý Viet thuận
Định lý Viet thuận trong phương trình được thể hiện như sau:
Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có hai nghiệm x1, x2 thì:
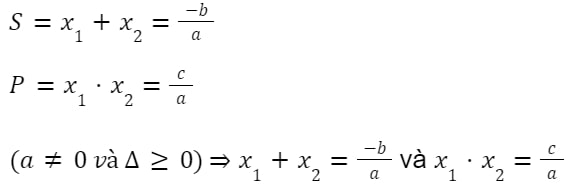
Hệ quả của phương trình: Ta có phương trình bậc 2 ax2 + bx + c=0 (1)
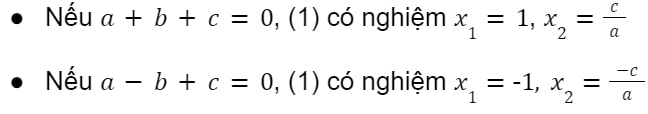
Định lý Viet đảo
Hệ thức Viet đảo trong phương trình được thể hiện là:
Nếu x1 và x2 thỏa mãn điều kiện S = x1 + x2 và P = x1.x2 thì chúng là nghiệm của phương trình t2 – st + p = 0. (Điều kiện: ∃ 2 số x1, x2 là S2 – 4P ≥ 4P ≥ 0).
Lưu ý trước khi áp dụng hệ thức Viet, ta cần tìm điều kiện để phương trình có 2 nghiệm là a ≠ 0 và Δ ≥ 0 (Δ’ ≥ 0).
Định lý Viet bậc 3
Phương trình ax3 + bx2 + cx + d = 0 có 3 nghiệm phân biệt x1, x2, x3. Khi đó:
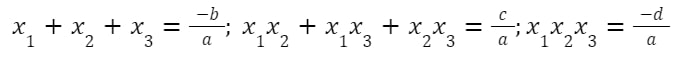
Ứng dụng của công thức Vi-et trong Toán học
Từ công thức tính Vi-ét, ta có thể áp dụng để tìm số a và số b khi biết S = a + b và P = a.b, khi đó ta cần giải phương trình x2 – Sx + P=0. Lúc này, a và b chính là nghiệm của phương trình.
Các ứng dụng của hệ thức Vi-et cụ thể bao gồm:
- Tính nhẩm nghiệm phương trình bậc 2: Với phương trình x2 – 5x + 6 = 0, ta có thể tính nhẩm nghiệm số nguyên của phương trình là 2 và 3 bởi 2 + 3 = 5 và 2 x 3 = 6.
- Tìm 2 số khi biết tích và tổng của chúng: Nếu tổng là S, tích là P thì 2 nghiệm phương trình gồm: x2 – Sx + P=0. (Điều kiện: S2 – 4P ≥ 0).
- Tính giá trị biểu thức đối xứng của 2 nghiệm phương trình bậc 2.
- Biến tam thức bậc 2 thành nhân tử: Nếu x1, x2 là nghiệm của đa thức f(x) = ax2 + bx + c có thể phân tích thành nhân tử f(x) = a(x – x1)(x – x2).
Kết luận
Kiến thức về công thức Viet và các ứng dụng được tổng hợp chi tiết. Học sinh có thể tham khảo và tìm hiểu về định lý này. Điều này giúp bạn biết cách áp dụng vào các bài toán từ cơ bản đến nâng cao. Việc nắm vững kiến thức cơ bản sẽ giúp bạn học tốt môn Toán hơn mỗi ngày.
Nguồn: https://congthuctoan.com
Danh mục: Đại số
Bài viết liên quan

Công thức số mũ và các quy tắc tính toán cơ bản trong toán học
Tìm hiểu chi tiết các công thức số mũ từ cơ bản đến nâng cao với cách giải thích đơn giản. Bao gồm quy tắc tính toán, mối quan hệ với căn thức, logarit và ứng dụng thực tế.

Công thức nghiệm pt bậc 2 và cách giải đơn giản cho học sinh yếu
Tìm hiểu chi tiết công thức nghiệm pt bậc 2 với cách giải đơn giản, dễ hiểu. Bao gồm công thức delta, phân loại nghiệm và phương pháp giải kèm bài tập mẫu có lời giải.

Tổng hợp công thức tổng hiệu và cách tính tổng dãy số cơ bản
Tìm hiểu các công thức tổng hiệu từ cơ bản đến nâng cao trong toán học. Hướng dẫn chi tiết cách tính tổng dãy số, tổng bình phương, cấp số cộng và các dãy số đặc biệt kèm bài tập mẫu.

Tổng hợp công thức hằng đẳng thức cơ bản và nâng cao chi tiết nhất
Tìm hiểu các công thức hằng đẳng thức từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập mẫu. Tổng hợp đầy đủ các dạng hằng đẳng thức quan trọng trong chương trình toán phổ thông.

Công thức logarit cơ bản và nâng cao dành cho học sinh yếu toán
Tìm hiểu các công thức logarit từ cơ bản đến nâng cao với cách giải thích đơn giản, dễ hiểu. Bao gồm công thức log, đạo hàm, tích phân kèm bài tập mẫu và ứng dụng thực tế.

Tổng hợp công thức lũy thừa và áp dụng giải bài tập đơn giản
Tìm hiểu các công thức lũy thừa từ cơ bản đến nâng cao với cách giải thích đơn giản, dễ hiểu. Bao gồm quy tắc, tính chất và bài tập mẫu chi tiết cho học sinh phổ thông.

