Công thức nhị thức Newton – Khái niệm, cách khai triển chính xác

Công thức nhị thức Newton được ứng dụng trong toán học với tác dụng khai triển hàm mũ. Có một sự thật cực kỳ thú vị là Newton không phải người đầu tiên tạo ra định lý này và thực hiện chứng minh nó.

Giải thích công thức nhị thức Newton là gì?

Công thức nhị thức Newton hay định lý nhị thức có tác dụng khai triển hàm mũ của tổng. Từ một nhị thức bậc n qua công thức này sẽ được khai triển thành một đa thức có dạng n+1.

Bạn đang xem: Công thức nhị thức Newton – Khái niệm, cách khai triển chính xác

Isaac Newton là người đầu tiên độc lập chứng minh định lý này vào năm 1665. Ông đưa toán học và cơ học lên một bước tiến mới với nhị thức trước khi James Gregory tìm ra và chứng minh lại vào năm 1670.

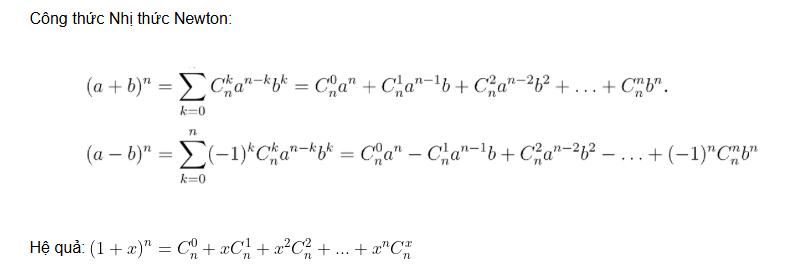
Từ biểu thức này có thể hiểu được:

• Các hạng tử n+1 sẽ có số mũ giảm dần từ n về 0 (trên a) và tăng dần từ 0 tới n (trên b);
• Tổng số mũ của a và b sau khi khai triển vẫn luôn bằng n;
• Các hệ số cách đều nhau.

Định lý này cũng đã được chứng minh, được thực hiện bằng phương pháp quy nạp:

Lý thuyết nhị thức Newton là gì?

Bên cạnh khái niệm công thức nhị thức Newton thì bạn cũng nên tìm hiểu đến nguồn gốc và cách khai triển của nhị thức mang tên nhà toán học lừng danh.

Trước tiên bạn hãy xem sơ đồ hình cây được chia sẻ ở dưới đây:

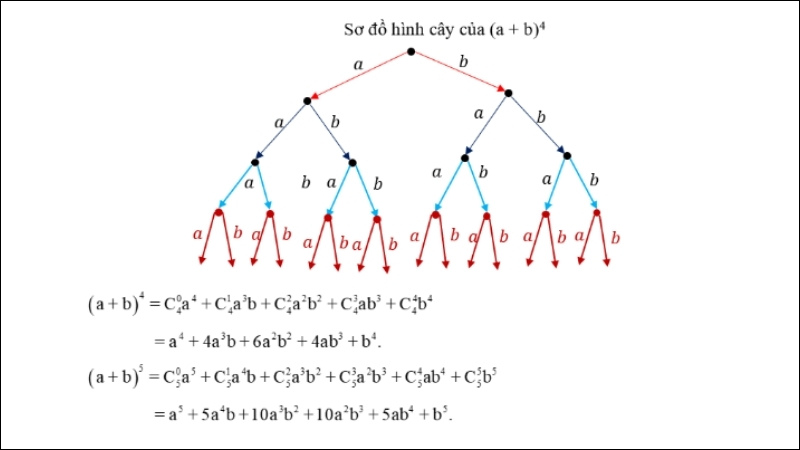
Từ hình cây này có thể thấy các tích nhận được mang tính đa thức, giống như cách lấy ra đơn thức từ mỗi đa thức xong lại nhân lại với nhau. Nếu để ý sẽ thấy tổng của chúng cho phép người sử dụng khai triển tích của các đa thức đã cho.

Đơn giản nhất có thể hình dung là: (a + b)^4 = (a + b)(a + b)(a + b)(a + b).

Bạn có thể tự xây dựng cho mình một sơ đồ hình cây dựa trên lý thuyết Newton theo các bước:

• Chọn một vị trí làm điểm gốc để phát triển các mũi tên, chúng đại diện cho các đơn thức của nhị thức thứ nhất;
• Ở mỗi đầu mũi tên đó lại kẻ tiếp các mũi tên khác tương ứng với đơn thức của nhị thức thứ hai;
• Bạn cứ làm tương tự như vậy cho đến nhị thức tương ứng với số mũ của hàm;
• Tại đầu của mũi tên cuối cùng, bạn ghi lại các tích tính từ điểm gốc đến đầu để hoàn thành.

Công thức khai triển nhị thức Newton cụ thể bạn nên biết

Để phục vụ cho việc tính toán đa dạng thì nhị thức có thể được khai triển thành:

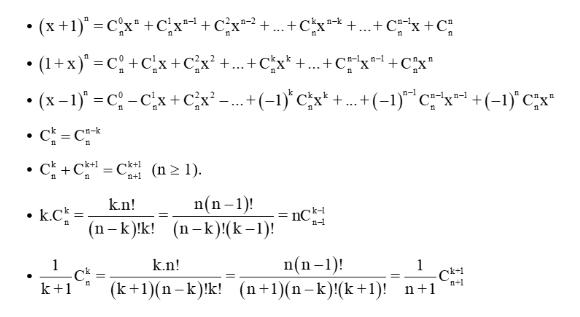
Khởi phát của định lý nhị thức Newton

Công thức nhị thức và công thức khai triển nhị thức Newton đã xuất hiện từ khá sớm, lần đầu tiên vào năm 200 TCN. Không rõ người đầu tiên tìm ra nhưng thông tin được lưu lại trong tài liệu của các nhà toán học Ấn Độ.

Tìm về phương Đông, người ta cũng thấy bảng số dưới dạng tam giác trong tác phẩm của Chu Sinh (Người Trung Hoa). Cấp triển khai đi từ 0 lên tới 8 và cho phép người đọc tìm được quy luật của các hàng mới.

Người ta còn tìm được tài liệu có nhắc tới định lý nhị thức viết bằng tiếng Ả Rập đó là “Chìa khóa số học” ra đời nửa đầu thế kỷ XV. Tác giả là Giêm Xit-Giaxedin Casi – Một nhà toán học đồng thời cũng là nhà thiên văn học.

Ông chỉ dẫn cho người đọc về việc thành lập các hàng kế tiếp của hệ số nhị thức. Tuy nhiên, tài liệu này vẫn chưa có nội dung chứng minh nên chưa được ứng dụng rộng rãi.

Định lý về nhị thức xuất hiện ở Châu Âu muộn hơn dưới dạng tam giác số học. Đó là công trình được công bố vào năm 1544 của nhà toán học Stiffel M. với việc khai triển lên tới cấp 17.

Gần một thế kỷ sau lần lượt là các công trình nghiên cứu của những nhà toán học người Anh và Pháp.

Nhưng phải đến năm 1665, Pascal mới đưa ra một luận văn rõ nét nhất về tam giác số học. Cũng vì thế mà hiện nay toán học có tam giác Pascal, định lý Pascal được ứng dụng rộng rãi.

Nguồn gốc tên gọi công thức nhị thức Newton

Từ nội dung ở trên chắc hẳn bạn rất thắc mắc tại sao cuối cùng lại có cái tên nhị thức Newton khi rõ ràng các công trình đã ra đời từ sớm.

Ông tìm ra định lý này từ năm 1665, đến năm 1676 thì gửi thư cho Chủ tịch Viện Hàn Lâm Hoàng gia Anh. Nhưng ở bức thư này ông chỉ mô tả công trình chứ không chứng minh rõ ràng.

Phải một thời gian sau đó thì nhà toán học đại tài này mới dẫn giải cách ông đi đến công thức. Đáng kinh ngạc là thời điểm mà ông bắt đầu tìm cách chứng minh là khi mới chỉ 22 tuổi.

Cái tên Newton được đặt cho một “công thức cũ” là vì cách mà ông ứng dụng nó. Ông không giới hạn ý tưởng của mình trong số mũ nguyên dương mà là số mũ bất kỳ, gồm cả số nguyên, phân số, số âm và số dương.

Điều này có ý nghĩa vô cùng lớn lao với sự phát triển của toán học, được các chuyên gia thời đó công nhận ngay lập tức và áp dụng vào đại số, giải tích.

Sau này khi Newton mất, nhị thức được khắc trên bia mộ của ông tại Tu viện Westminster.

Các dạng toán phổ biến áp dụng nhị thức Newton

Xem thêm : Lý thuyết công thức Bernoulli và các ứng dụng trong toán học phổ thông

Ở chương trình học phổ thông sẽ không xuất hiện tất cả các dạng này vì có một số khá khó. Tuy nhiên, bạn vẫn nên tìm hiểu kỹ càng để ôn luyện, hiểu sâu hơn về định lý quan trọng này.

1/ Bài toán tìm số hạng thứ k

Cách giải không quá phức tạp, đầu tiên bạn hãy cứ khai triển ra để tìm số hạng tổng quát đã. Sau đó bạn thực hiện giải phương trình có hai số mỹ bằng nhau để tìm được k tương ứng với số hạng Xm thỏa:

k = (m – np) / (p – q) với m = np – pk + qk

Trường hợp k>n hoặc là số thập phân thì khai triển chắc chắn không có Xm và hệ số phải tìm sẽ bằng 0.

2/ Chứng minh đẳng thức

Bạn cần đảm bảo công thức nhị thức Newton được khai triển rồi suy ra điều phải chứng minh. Đề bài thường sẽ cho a, b, n bằng các giá trị nào để từ đó rút ra đẳng thức.

3/ Tìm hệ số trong khai triển nhị thức

Đề bài thường yêu cầu tìm hệ số Xk nên dĩ nhiên phải dùng công thức khai triển được cập nhật ở trên.

4/ Ứng dụng công thức nhị thức Newton vào tổ hợp

Trong khai triển (a + x)n có a là hằng số, cần dùng các phép biến đổi đại số để tính. Bài toán có thể xuất hiện trong tích phân, đạo hàm với x là một giá trị cụ thể.

Bài tập về nhị thức Newton và lời giải chi tiết

Đề bài 1: Hãy khai triển hai đa thức:

1. (2x – 1)^4
2. (x + 4)^5 + (x – 4)^5

=> Cách giải:

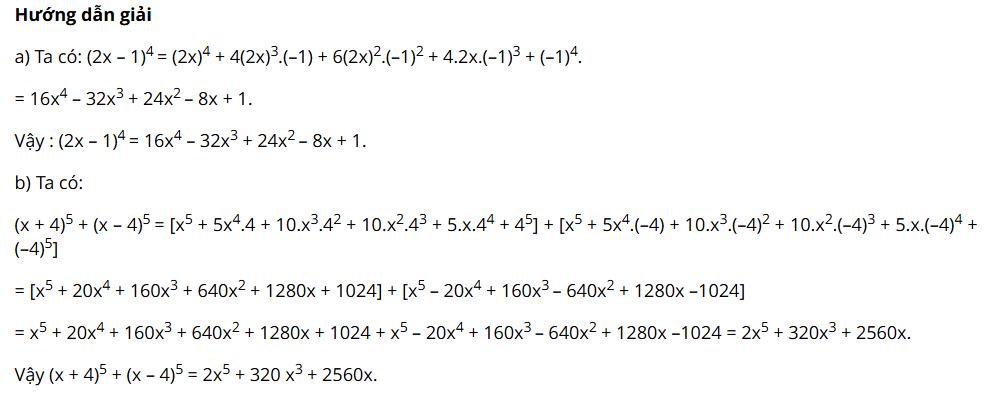
Đề bài 2: Hãy tìm hệ số x5 trong biểu thức:

P = (x + 1) + 2(x + 1)2 + … + 8(x + 1)8.

=> Cách giải:

Kết luận

Công thức nhị thức Newton là một phần quan trọng của toán học, hỗ trợ rất nhiều trong quá trình giải bài tập tổ hợp, đạo hàm, tích phân,… Bạn cần nắm chắc định lý này và công thức khai triển để ứng dụng hiệu quả.

Nguồn: https://congthuctoan.com
Danh mục: Xác suất - Thống kê